重拾分数计算 优化运算步骤

【摘要】本文论述指导学生用分数计算优化运算步骤的方法，通过观察、分析具体教学片段，指出学生在运算中面临的问题，建议利用分数计算简化运算过程，提高学生的计算能力。

【关键词】小学数学 分数计算 整体性 运算步骤

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2019）09A-0099-02

计算表面上看起来很简单，只要学生掌握了基本的运算法则，就可以进行运算。但在面对一些计算步骤多、数据量大的问题时，学生经常出现畏惧计算或不愿计算的情况。怎样帮助学生提高运算能力呢？笔者对小学高年级计算练习进行调查后发现，分数计算相对于整数计算和小数计算具有运算的优势，利用分数计算可以把握计算对象的整体性，使得运算过程简便。

一、问题由来：一阵议论声打破了备课的“理所当然”

小学高年级数学学习侧重于综合应用数学知识解决实际问题，练习中存在大量的计算问题。然而，学生常常为计算而苦恼。

（一）教材情景及简析

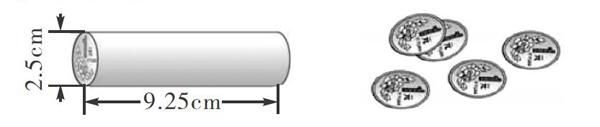
苏教版小學数学教材六年级下册第二单元中有这样一个问题：银行通常将50枚1元硬币摞在一起，用纸卷成圆柱形（如下图）。你能算出1枚1元硬币的体积大约是多少立方厘米吗？（得数保留一位小数）

问题要求1枚1元硬币的体积，可以先算出50枚1元硬币的体积，也可以先算出1枚1元硬币的厚度，题目意图在于让学生体会灵活运用圆柱体积公式解决实际问题的过程。

（二）课堂教与学的情况

师：你们准备如何解决这个问题？

生1：先求出大圆柱体积，再除以50，算出1枚硬币的体积。

师：同意他的想法吗？

生（齐）：同意。

师：还有别的想法吗？

生2：我们也可以先算出1枚硬币的厚度，再求1枚硬币的体积。

师：这样可行吗？

生（齐）：可行。

师：选择你喜欢的方法，列式计算出1枚硬币的体积。

（课堂状态：教室里一片安静。过了一会儿，个别学生在交谈。接着，议论声音变大了）

师：怎么回事？

生3：太难算了！

生4：有四位小数计算，老师你看，有“3.14×1.5625”。

生5：要是有计算器就好了！

（三）教师对学生生成的质疑

学生的一句“要是有计算器就好了”，让笔者意识到，学生的计算肯定哪儿出了问题，同时也意识到课前备课似乎忽略了什么。笔者打开预设的教案，预设解题过程是这样的：

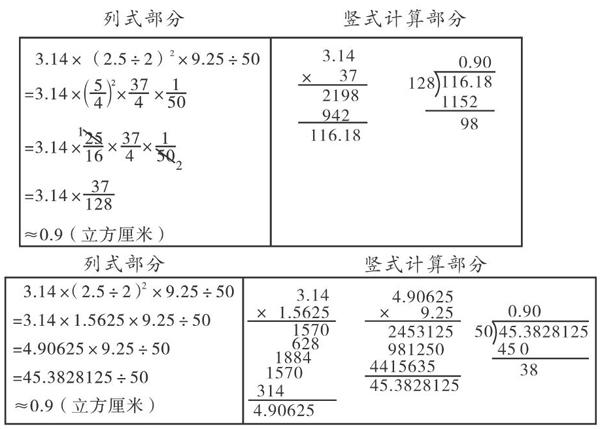
预设列式采取综合算式形式，转化为分数形式避开小数运算，竖式计算涉及的小数计算也是学生熟悉的3.14的乘积，最后小数除法关键步骤其实只有一步，所以这样的预设并没有引起笔者过多的注意，但学生的表现却打破了笔者备课的“理所当然”。

（四）教师直面学生的生成

笔者思考片刻，直接转向学生提出的计算问题，踏踏实实地在黑板上计算出来，虽然计算量较大，但能够计算出来。过程如下：

紧接着，笔者给学生提了一个问题：“我们能否将算式中的数处理一下，优化计算过程，让计算不那么繁杂。正好老师这有一种方法，你们觉得这样的计算过程怎么样？”（出示预设算法）

分析：教学是教师教与学生学的有机结合，教学过程中，学生的学有发生，随之教师的教应生发生，久而反复，方可教学相长。上述环节中，教师没有直接抛弃学生的计算方法，而是直面学生的问题所在，解决难计算的问题，帮学生克服计算困难，树立计算信心。同时，考虑到学生思维与教师思维的不一致，对比是学生与教师思维链接最好的桥梁，因此，笔者采取对比的形式呈现教师的计算过程，给学生自我优化及汲取运算方法的空间。

二、原因分析：这阵议论声究竟为何而来

课堂上突如其来的一阵议论声，让原本平静的练习课变得不平静，这不平静的背后究竟隐藏了什么？下面笔者以问题的形式寻找答案。

问题1：学生到底会不会算？

题目中的计算有平方和小数的多位数乘除法，属于小学阶段计算内容，因此，学生是会计算的。

问题2：学生为什么不算？

既然学生会算，但学生没有算，问题出在哪儿？回顾学生的计算过程，较为复杂的步骤有3.14×1.5625和4.90625×9.25两步，这两步都是多位数小数乘法，其中3.14×1.5625的计算过程需要计算6步（5步乘法、1步加法），4.90625×9.25的计算过程需要4步，每一步的数据量都很大，数据量最大的有9位数。像这样计算步骤多、数据位数大的计算确实有一定的计算难度，这里计算步骤多、数据位数大主要源于题目信息中的数字形式——小数。笔者对大量乘法计算问题出错原因进行调查后发现，问题类型对学生的影响不大，数字形式是关键所在，以此看来，数字的形式是学生畏惧、不愿计算的主要原因。

问题3：如何解决学生的不愿意算？

教师预设算法的步骤并不比学生算法的步骤少，但过程中很少涉及竖式计算，且竖式计算量小，易于计算，这是由于教师将算式中的小数转化为分数，利用分数约分进行化简，减少计算步骤、缩小数据量，最后只要计算3.14×37÷128即可。就这道题来看，小数转化为分数可以有效解决学生不愿意算的问题。

三、教学启示：重新认识分数计算

为什么小数转化为分数就可以解决学生的问题？这需要我们重新认识分数计算。

（一）与整数计算和小数计算相比分数计算所具备的优势

小学阶段所涉及的运算对象有三类：整数运算、小数运算和分数运算。与整数运算、小数运算相比，分数运算具有的优势具体体现在分数可以与小数、整数相互转化形式，分数计算知识与除法、比的知识相通。例如：将一个直径是3厘米的圆放大成半径为6厘米的圆，放大后的圆的面积与放大前圆的面积的比是多少？

此过程利用比的意义、分数除法等知识，在整数范围里通过约分得出结果（如右图左）。如果将“直径3厘米”用小数求出半径为1.5厘米，按照题意，这时需要通过小数除法计算，相比之下，利用分数计算具有优势。

（二）分数计算关注计算对象的整体性

在混合运算中，分数运算侧重于计算对象的整体性，以上面例题为例（如下图），左边是利用分数计算过程，计算中将3.14后面的数据看成一个整体，借助分数约分进行整体计算，突出计算对象之间的关系。再看图中右边的计算过程，在混合四则运算的顺序下，从左往右依次计算，表现出纯粹的计算性。由此看来，分数计算过程表现出计算对象的运算特性。在日常教学中，教师应潜移默化地培养学生重运算的意识。利用分数计算过程，需要考虑计算对象之间的关系，利用约分前需要做好观察、思考、转化等准备工作（发现25，并将25与50约分），更能体现出计算的数学思维，具有良好数感的学生能够更好地把握计算对象的整体性。

（三）分数计算易于呈现计算的简化步骤

小学高年级学生在计算中不仅会思考问题的解题思路，而且还会考虑是否存在简便的计算步骤，由于分数计算关注计算对象的整体性，使得计算过程中简化的步骤更利于发现。例如，苏教版小学数学教材六年级下册第六单元练习八第7题：小青家到梅花山的路程大约4.2千米，以12千米/时的速度骑自行车前往，需要多少分鐘到达？解答过程如下，第二种解题过程更利于学生发现计算中的简便因素（12与60约分）。

小学是学生从具体运算向形式运算过渡的阶段，分数计算过程关注计算对象的整体性，突显计算对象的内在关系，符合形式运算的特质。分数计算通常涉及分数加减法通分、分数乘法约分和分数除法中倒数等，这些问题中蕴涵着丰富的数学形式结构，通过解决分数计算问题有助于学生顺利完成这种过渡。

【参考文献】

[1]郜舒竹.小学数学这样教[M].上海：华东师范大学出版社，2015

[2]史宁中.义务教育数学课程标准（2011年版）解读[M].北京：北京师范大学出版，2012

[3]郑毓信.小学数学概念与思维教学[M].南京：江苏凤凰教育出版社，2014

[4]鮑建生，周超.数学学习的心理基础与过程[M].上海：上海教育出版社，2009

作者简介：谢云龙（1984— ），男，江苏南京人，小学一级教师，大学本科学历，江北新区小学数学学科带头人，研究方向：小学数学教学。

（责编 雷 靖）