基于响应面-遗传算法的CSP焊点随机振动应力与回波损耗双目标优化设计
2019-11-20路良坤黄春跃李天明
路良坤,黄春跃,梁 颖,李天明
(1.桂林电子科技大学 机电工程学院,桂林 541004;2.成都航空职业技术学院 电子工程系,成都 610021;3.桂林航天工业学院 汽车与动力工程系,桂林 541004)
随着电子产品对小型化、多功能化、高集成度化及低成本需求日益增长,对集成电路芯片封装技术提出了更小尺寸、更好力学、热学及电磁性能的要求。与球栅阵列(Ball grid array,BGA)封装技术相比,CSP封装技术占用印制板的面积更小,芯片面积与封装面积之比接近1∶1的理想情况,可广泛用于微薄型电子产品中,在相同的封装尺寸时可有更多的I/O数,使组装密度进一步提高,因此符合电子产品小型化的发展潮流,是极具市场竞争力的高密度封装形式。
在CSP封装中,CSP焊点起着机械支撑和电气连接的关键作用,当CSP芯片应用于包括机载、车载和船载通讯电子产品的情况时,随机振动载荷成为造成CSP焊点疲劳失效,据美国空军统计,超过20%的电子器件是由于振动导致失效的[1];作为应用于通讯产品中的CSP焊点面临着在高频条件下因自身寄生电容和自感而造成的信号在传输过程中回波损耗增大,从而导致出现信号完整性问题。
虽然振动冲击引起的焊点可靠性问题日益引起人们的重视,但国内关于CSP焊点随机振动的研究尚不多见,仅王红芳等[2]通过建立倒装焊点电子组件模型,研究了振动环境对焊点可靠性的影响;韦何耕等[3]研究了PBGA焊点结构方式、焊点材料、底充胶弹性模量和密度在随机振动环境下对叠层无铅焊点可靠性的影响。在国外,Kim等[4]针对PBGA电子产品在随机振动载荷下的可靠性进行分析研究;Tang等[5]板级组件产品在随机振动下的失效模式进行分类。针对焊点信号完整性问题,国内外学者也开展了相应的研究工作:黄春跃等[6]基于HFSS建立单个焊点模型,研究了信号频率对焊点完整性的影响,发现频率增加会导致焊点信号完整性变差;石光耀等[7]分析了焊点形态和布局对信号完整性的影响,结果表明焊点的尺寸参数对焊点的信号完整性有着不可忽略的影响;Ndip等[8]研究了焊点阻抗对焊点信号完整性影响,发现随着频率升高焊点内阻抗会增加,进而导致焊点信号完整性变差。从以上国内外学者对焊点振动可靠性和信号完整性所展开的研究工作表明了对焊点进行随机振动分析和信号完整性分析研究具有重要意义。已有研究成果也反映出目前国内外学者只局限于对焊点进行单方面振动分析研究或单方面信号完整性进究,没有兼顾焊点振动可靠性和信号完整性,而实际应用条件下,焊点则是必须同时具备振动可靠性和良好的电气传输性能的,因此,有必要展开振动分析与信号完整性分析相结合的研究,以确保焊点同时具备振动可靠性和优良的信号传输性能。由此,本文以CSP焊点为研究对象,对CSP焊点进行随机振动加载仿真分析,得到焊点随机振动应力;随后对CSP焊点进行电磁仿真分析,获取焊点回波损耗(即S11值);在此基础上采用响应面和遗传算法相结合的方法进行以CSP焊点随机振动应力和回波损耗同时降低为目标的双目标优化设计,得到CSP焊点随机振动应力和回波损耗同时降低的最优参数水平组合,并对最优参数水平组合加以试验验证,实现了CSP焊点振动应力和回波损耗同时降低的优化目标,为同时提高CSP焊点可靠性和信号完整性提供理论指导。
1 CSP焊点随机振动应力应变有限元分析
1.1 CSP焊点有限元分析模型
本文采用有限元分析方法对CSP焊点进行随机随机振动环境下应力应变。为了确保CSP焊点模型在形态上的准确性,采用基于最小能量原理的Surface Evolver软件对CSP焊点形态进行预测之后,得到焊点直径和焊点高度等几何形态参数,将得到的形态参数在有限元分析软件ANSYS中建模,所模拟的单个CSP焊点三维形态如图1所示。采用ANSYS软件建立的CSP焊点有限元分析整体模型如图2所示。
图1 CSP焊点三维形态Fig.1 Three dimensional shape of CSP solder joint
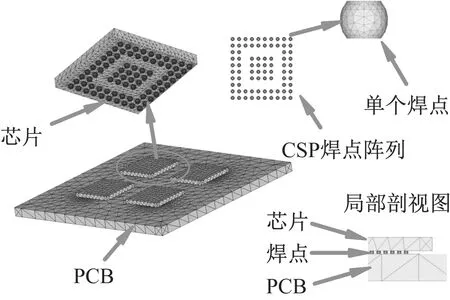
图2 CSP焊点有限元分析模型Fig.2 Finite element model of CSP package
模型中PCB尺寸为40 mm×40 mm×1.8 mm,4个CSP芯片尺寸均为7 mm×7 mm×0.75 mm;单个芯片焊点为10×10非全阵列,焊点数80个,焊点高度0.2 mm,焊点直径0.3 mm,焊点间距0.65 mm,焊盘直径0.24 mm。进行有限元网格划分时CSP焊点使用VISCO107黏塑性实体单元,其他结构使用SOLID45实体单元,整个模型网格划分后单元数为308 565个。模型中各部分的材料参数如表1所示。
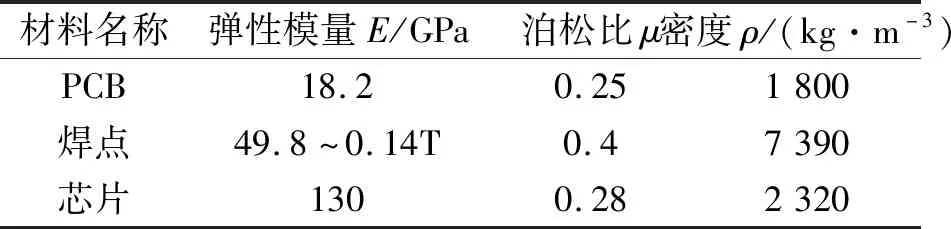
表1 材料参数Tab.1 Material parameters
本文随机振动分析所用PSD加速度功率谱条件来源于美国军标MIL-STD NAVMAT P9492,如图3所示。当随机振动频率在20~80 Hz时,曲线上升斜率为+3 dB/oct,对应的加速度功率谱密度幅值范围为0.01~0.04 g2/Hz,80 Hz时为0.04 g2/Hz;当随机振动频率在80~350 Hz时,对应的加速度功率谱密度幅值为0.04 g2/Hz,当随机振动频率在350~2 000 Hz时,曲线以-3 dB/cot的斜率下降,对应的加速度功率谱密度幅值范围为0.04~0.01 g2/Hz。

图3 随机振动加速功率谱加密度曲线Fig.3 Acceleration power spectral density curve with random vibration
1.2 CSP焊点应力应变有限元分析
在ANSYS软件中,对CSP焊点进行随机振动有限元时,在PCB板底面四个角点处施加全约束,先对CSP焊点有限元模型进行模态分析,再进行PSD谱分析[9]。通过有限元分析得出CSP焊点应力应变分布情况如图4和图5所示。图4为CSP焊点阵列应力分布情况,最大等效应力焊点位于右上侧位置芯片的右下角焊点,最大等效应力为9.63×10-2MPa;图5为CSP焊点阵列应变分布情况,最大等效应变0.318×10-5。由图4和图5可见,随机振动载荷下,CSP焊点阵列内不同焊点的应力应变大小均不同,位于中心的焊点等效应力应变最小,从中心焊点到边缘焊点应力应变逐渐增加,离中心最远处的焊点等效应力应变最大。因此离焊点阵列中心最远处的焊点为关键焊点,振动所致疲劳裂纹优先在该焊点处产生,从而造成CSP器件失效。

图4 CSP焊点等效应力Fig.4 Equivalent stress of CSP solder joints
CSP焊点的焊点直径、焊点高度和焊盘直径等几何形态参数的变化会对焊点内随机振动应力应产生相应的影响。为分析CSP焊点形态参数变化对焊点随机振动应力应变的影响,在只改变某一个形态参数的条件下,建立单一形态参数变化的有限元分析模型并进行随机振动加载仿真分析,得到相应的应力应变,从而可以对比分析某一个焊点形态参数单一变化时对随机振动应力应变的影响规律。

图5 CSP焊点等效塑性应变Fig.5 Equivalent plastic strain of CSP solder joints
在分别只改变CSP焊点的焊点直径和焊点高度情况下,焊点内应力应变数据如表2所示。从表2可知,随着CSP焊点直径的增加,焊点内最大应力应变均随之相应增加,适当减小焊点直径有利于减小焊点内应力应变;随着CSP焊点高度的增加,焊点内最大应力应变均总体呈现减小趋势,适当增加焊点高度有利于减小焊点内的应力应变。

表2 焊点直径和焊点高度对焊点随机振动应力影响Tab.2 Effects of solder joint diameter and solder joint height on random vibration stress of solder joints
2 CSP焊点三维电磁仿真分析
2.1 CSP焊点电磁仿真分析模型
利用HFSS软件建立与1.1节相同尺寸的焊点模型,如图6所示。分析时定义相关辐射边界条件,焊点上下焊盘处添加波端口激励,设定频率变化范围为1~10 GHz,进行仿真分析后即可获取CSP焊点的回波损耗值,即S11参数,以回波损耗值作为CSP焊点信号完整性评价指标,通常回波损耗值越小则说明信号传输过程中信号完整性越好。
图6 CSP焊点电磁仿真模型Fig.6 Electromagnetic simulation model of CSP solder joint
2.2 CSP焊点电磁仿真结果分析
对图6所示CSP焊点模型进行回波损耗仿真分析,分析结果如图7和表3所示。图7所示为回波损耗变化趋势图,由图可见随着频率的增加回波损耗值会发生变化;表3所示为不同频率条件下回波损耗值,从表3可以见频率为1 GHz时,焊点S11值为-12.826 dB;当频率升至10 GHz时,S11值为-12.821 dB,即随着信号频率的升高,焊点的回波损耗值也逐渐增大,说明随着信号频率的升高,焊点信号完整性变差。这是由于在高频条件下焊点的寄生电容不容忽略,寄生电容使信号上升沿减慢,降低信号传输速度,且焊点在高频条件下由于高频趋肤效应[10]导致焊点内电阻增大,从而导致阻抗增加,这些变化会造成焊点内回波损耗增加,从而使焊点信号完整性变差。
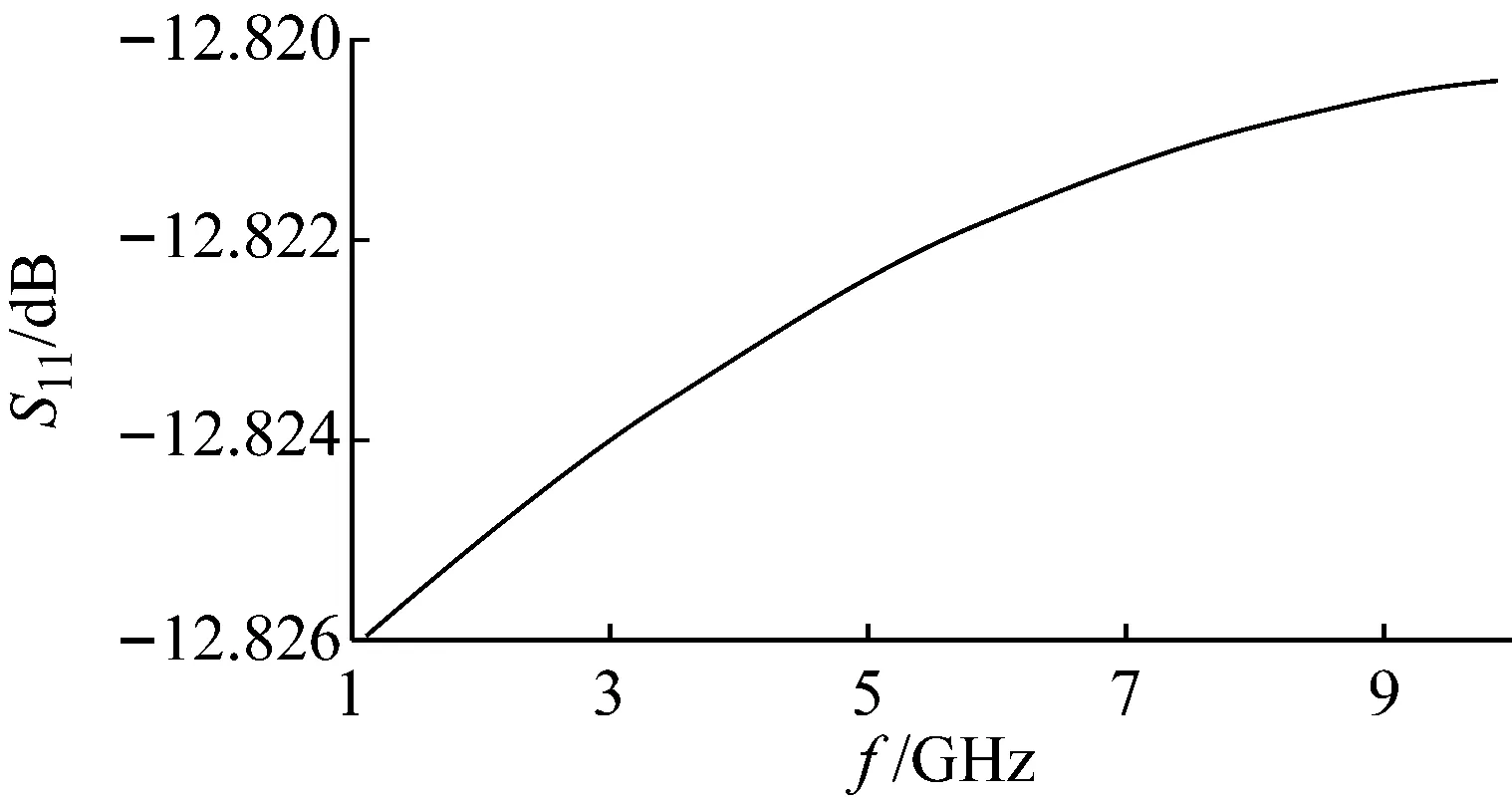
图7 频率对回波损耗影响规律Fig.7 The influence of frequency on return loss
表3 不同频率条件下回拨损耗值
Tab.3 Return loss value under different frequency

频率f/GHzS11值/dB频率f/GHzS11值/dB1-12.82606-12.82212-12.82497-12.82183-12.82438-12.82154-12.82339-12.82125-12.822410-12.8209
与CSP焊点的焊点直径、焊点高度和焊盘直径等几何形态参数的变化会对焊点随机振动应力应会产生影响相类似,CSP焊点形态参数的变化同样会的焊点的信号完整性产生影响,为了分析CSP焊点形态参数变化对焊点信号完整性的影响,在只改变某一个形态参数而其他参数不变的条件下,建立单一形态参数变化下的电磁仿真模型并进行仿真分析,得到相应的回波损耗,从而对比分析焊点形态参数单一变化对其信号完整性影响的规律。
在分别只单一改变CSP焊点的焊点直径和焊点高度的情况下,焊点回波损耗数据如表4所示(为了便于比较,统一取频率为5 GHz时的回波损耗值来)。由表4可见,回波损耗随焊点直径的增大而增大,也随焊点高度的增大而增大。
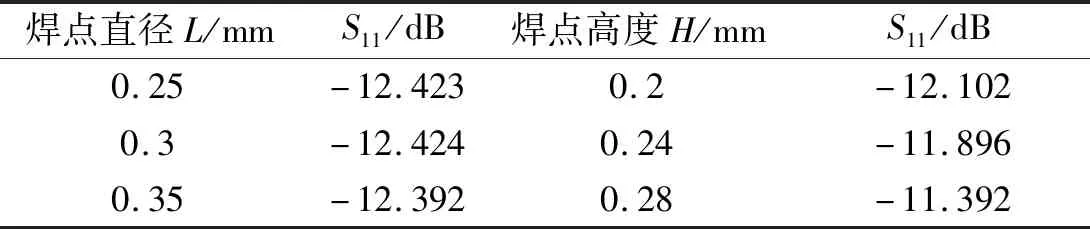
表4 焊点直径和焊点高度对回波损耗影响Tab.4 Effect of solder diameter and solder joint height on return loss
3 基于响应面法和遗传算法的CSP焊点形态参数优化
由本文前两节分析可知焊点形态参数变化对随机振动应力和回波损耗均会产生相应影响,为了获得CSP焊点随机振动应力和回波损耗同时降低的CSP焊点形态,本文将采用响应曲面法与遗传算法相结合,对形态参数进行回归分析,以实现CSP焊点随机振动应力和回波损耗同时降低,获取CSP焊点的最优参数水平组合。
3.1 响应面法
响应面法(Response Surface Method,RSM)是一种用近似的函数关系式表示变量与目标函数之间关系的拟合设计方法[11]。该方法首先利用实验设计建立因素的若干实验组合,分别对各组合进行实验并获得相应的目标值,然后选择合适的数学模型对因素与目标结果表示,再运用最小二乘原理求得模型中未知系数,最后得到变量与结果的拟合函数表达式。
3.2 仿真试验设计
选取CSP焊点形态结构参数:焊点直径L、焊点高度H、焊盘直径D。3个因素分别选取3个水平值,各水平取值如表5所示(因素是指影响试验结果的原因,水平是指试验中因素所设定的不同量或质的级别)。
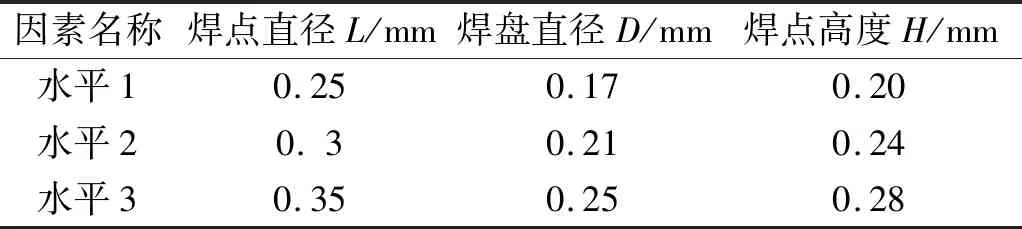
表5 CSP焊点结构参数因素水平表Tab.5 Factors and levels of CSP solder
为了用较少的实验次数获得较精准的实验结果,本文选用Box-Behnken 设计方法[12]得到CSP焊点结构参数的因素水平组合,如表6所示,表中共有17组完整传输路径参数水平组合,其中12组为分析因子,5组为零点因子,即参数水平组合相同,用于试验误差估计。分别根据这17组参数水平组合建立对应仿真分析模型,仿真分析后获得随机振动应力值和回波损耗值分别如表6最后两列所示。
3.3 建立双目标模型
RSM可以选择可选用的数学模型比较多,其中包括一元线性回归模型、多元线性回归模型和多项式回归模型等。根据微积分知识,任一函数都可由若干个多项式分段近似表示,因此在实际问题中,无论变量和结果间关系复杂程度如何,总可以用多项式回归来分析计算,由于本文设计变量为3个且变量与目标之间函数关系为非线性,结合表6的试验样本数,选用基于泰勒展开式的二阶多项式型
(1)

随机振动应力F
F=-9.07-1.18×L-0.94×H-0.06×D-
3.12×L2+0.46×H2-3.09×D2+2.33×
L×H+4.38×L×D-0.62×H×D
(2)
回波损耗S11
S11=-13.48-1.15×L+0.47×H+1.04×D+
2.51×L2-0.67×H2+1.43×D2-0.45×
L×H-2.69×L×D+0.35×H×D
(3)
在式(2)和式(3)中,L、H、D分别代表CSP焊点直径、焊点高度和焊点焊盘直径。

表6 响应曲面组合与分析结果Tab.6 Response surface combination and analysis results
3.4 基于遗传算法的随机振动应力和回波损耗双目标优化
遗传算法利用生物进化思想对求解域逐步筛选比较最终搜索得到问题优,该算法能准确预测出回归方程的目标函数值[13]。本文采用遗传算法对CSP焊点进行随机振动应力和回波损耗双目标化,以获取满足随机振动应力和回波损耗同时降低的CSP焊点形态参数水平组合。
依据影响焊点回波损耗的焊点形态参数:即焊点直径L、焊点高度H和焊盘直径D,结合3.3节得到焊点形态参数与随机振动应力、回波损耗的二次多项式回归方程。在此基础上将响应曲面所得拟合函数与遗传算法相结合,通过MATLAB遗传算法工具箱对随机振动应力F、回波损耗S11回归方程进行参数优化,并利用该算法得到随机振动应力和回波损耗的预测值,遗传算法参数设置如表7所示。
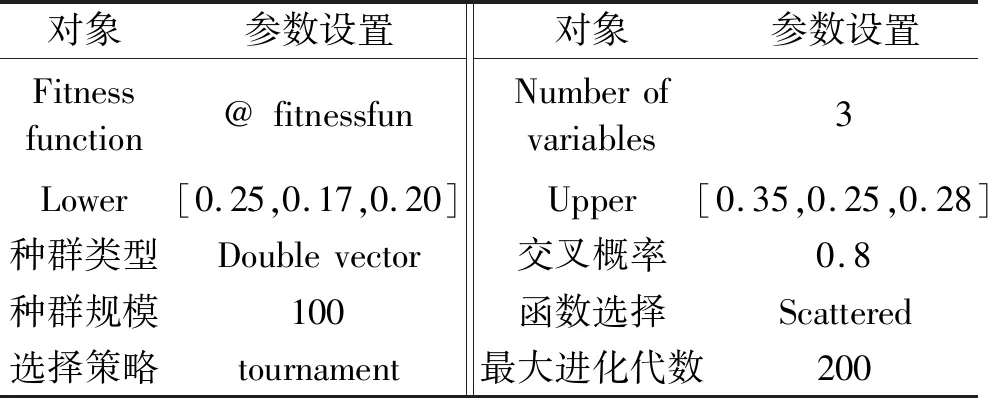
表7 遗传算法参数设置表Tab.7 Genetic algorithm parameter setting table
设置好相应参数,在MATLAB中运行编辑好的程序,得到如图8所示的随机振动应力与回波损耗之间的帕累托前沿(Pareto Front),即通过gamultiobj求解后得到的30组Pareto Front 优化解(非劣解)的分布,由图可见30组优化解分布相对均匀,优化解比较接近前沿面,可见优化解相对响应曲面数据而言有较大的改进。

图8 帕累托前沿图Fig.8 Picture of pareto frontal
在进行CSP焊点随机振动应力值及回波损耗双目标优化过程中,为了同时提高CSP焊点的可靠性和信号完整性,即应力值、回波损耗值越小越好,本文将CSP焊点各权重系数设置为λσ=0.5、λδ=0.5(在不同领域对随机振动应力和回波损耗的侧重点不同,可设置不同的权重系数),令评价函数P=λσ×F+λδ×S11,分别求得30组优化解的函数P的值如表8所示,以评价函数P值最小表征该组合应力值、回波损耗值同时降低的程度最高,由表8可知,权重系数为λσ=0.5、λδ=0.5时,在全部30组优化解中的第9组的评价函数P的值最小,表明该组的结构参数组合在所有优化解中应力值和回波损耗值同时降低的程度最高,即第九组为权重系数为λσ=0.5、λδ=0.5时的最优解。在MATLAB软件的结果文件中查看可知此第9组优化解所对应的焊点直径为0.35 mm、焊点高度为0.2 mm、焊盘直径为0.17 mm(该组参数水平组合即为最优结构参数水平组合),随机振动应力预测值为8.767 3×10-2MPa,回波损耗预测值为-13.186 8 dB。

表8 30组非劣解评价函数值Tab.8 Evaluation function value of 30 groups of non-inferior solutions
4 CSP焊点双目标优化最优参数组合验证
4.1 最优参数组合仿真验证
基于3.4节中由响应面法-遗传算法得出最优CSP焊点结构参数水平组合,即焊点直径为0.35 mm、焊点高度为0.2 mm、下焊盘直径为0.17 mm,在设定其他条件不变的情况下,根据以上CSP焊点参数重新建立分析模型,进行仿真分析,得到随机振动条件下CSP焊点应力结果如图9所示;同时再建立最优组合的电磁仿真模型进行仿真,得到焊点不同频率下的回波损耗如图10所示。
由图9可见,在随机振动载荷下CSP焊点应力值为8.57×10-2MPa,与遗传算法预测值8.77×10-2MPa相比仅相差0.22×10-2MPa,比优化前降低1.06×10-2MPa,下降程度为11%;由图10可见,当信号频率为5 GHz时,回波损耗值为-13.179 6 dB,与遗传算法预测值相差仅0.004 dB,比优化前降低了0.357 2 dB,下降程度为2.78%。
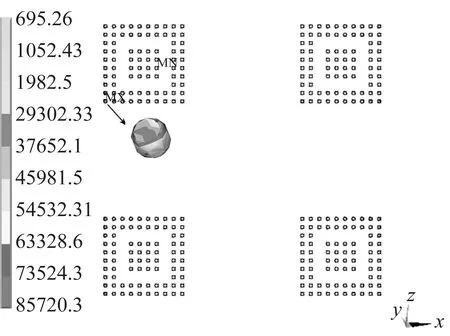
图9 最优组合CSP焊点应力分布图Fig.9 Stress distribution of CSP solder joint optimal combination
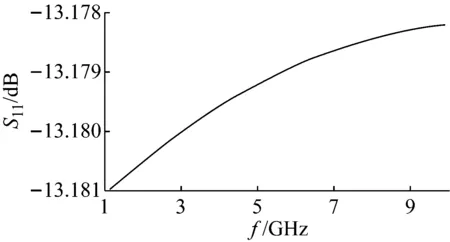
图10 最优组合CSP焊点回波损耗变化图Fig.10 Return loss of CSP solder joint optimal combination
此外,通过与表6中所示的其他水平组合方案相比可知,优化后的水平组合兼顾了随机振动应力和回波损耗(如第17组方案虽然随机振动应力最小但回波损耗较高;第4组实验方案回波损耗最低但随机振动应力较大),与仅考虑随机振动应力最小或回波损耗最小的参数水平组合相比,优化后的水平组合实现了CSP焊点的随机振动应力和回波损耗同时优化。说明遗传算法对应力值预测相对准确,证明了响应面-遗传算法相结合得到的优化组合使CSP焊点的应力值和回波损耗值均明显减小,实现了CSP焊点应力和回波损耗的优化。
4.2 CSP焊点最优参数水平组合回波损耗实验验证
为了验证经响应面-遗传算法分析所得到的CSP焊点最优参数水平组合的回波损耗是否降低,本文制作了两种不同结构参数水平组合的CSP焊点回波损耗测试样件,其中一种样件的结构参数水平组合与本文2.1节所述基本结构模型一致,而另一种样件的结构参数则为经过响应面-遗传算法分析所得到的最优参数水平组合,通过对两种不同结构参数水平组合的CSP焊点样件进行回波损耗实验测试,以验证响应面-遗传算法分析结果的准确性。
图11所示为具有最优参数水平组合结构参数的CSP焊点回波损耗测试样件,CSP焊点位于两印制电路板之间,在焊接过程中通过将0.2 mm厚度的塞尺(厚薄规)置于两电路板之间,以实现最优参数水平组合结构参数的CSP焊点回波损耗测试样件的制作,保证了焊点高度准确。CSP焊点的回波损耗测试实验测量系统连接图如图12所示,CSP焊点的两端通过测试样件上的两个微波高频连接器(Sub-Miniature-A,SMA)与矢量网络分析仪相连,采用矢量网络分析仪测量焊点的回波损耗值S11。所采用的矢量网络分析仪为Agilent公司生产,其型号为N5230C,工作频段为10 MHz~40 GHz。

图11 CSP焊点回波损耗测试样件Fig.11 The return loss test sample of micro-scale CSP solder joint

图12 CSP焊点回波损耗测试系统连接图Fig.12 Picture of the CSP solder joint return loss test
利用网络矢量分析仪分别测量两种不同结构参数水平组合的CSP焊点回波损耗测试样件,测量结果如图13所示。
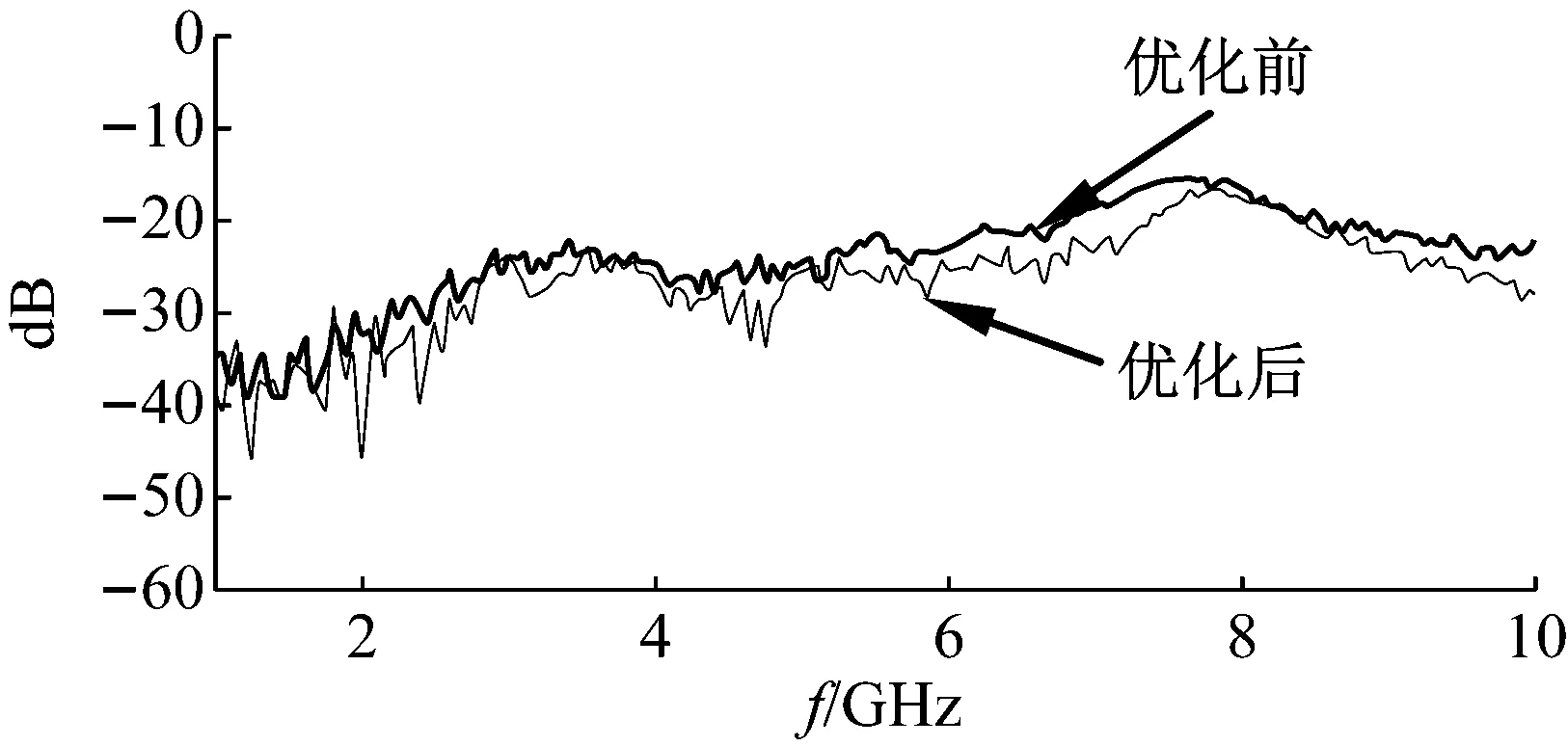
图13 不同结构参数水平组合焊点回波损耗测试结果Fig.13 The return loss test results of different structure parameters
由图13可知,实测CSP焊点回波损耗的变化曲线与仿真曲线变化趋势一致,但总体趋势与仿真结果吻合,这一方面是由于样件在制作过程中确实存在加工误差和测量环境等方面的影响,另一方面仿真是在理想环境下进行计算求解,而实测过程中由于SMA接头、微带线及测量连接线缆等部分引入部分损耗,使得信号强度减弱,从而降低了反射回来的电磁波,导致实测结果与仿真结果相差较大[14-15]。在频率为5 GHz时,基本结构和最优结构焊点的回波损耗值分别为-24.32 dB和-25.37 dB,实测结果低于仿真结果,优化后焊点回波损耗值比优化前降低了1.05 dB,由此可知,采用响应面法和遗传算法相结合的方法优化CSP焊点信号完整性是有效的。
5 结 论
对CSP焊点进行随机振动应力和回波损耗优化进行了研究,寻找出一组使CSP焊点随机振动应力和回波损耗同时降低的最优参数组合,优化后CSP焊点最大等效应力下降了11%的同时回波损耗降低了2.78%,试验实测焊点优化后回波损耗比优化前降低了1.05 dB,证明响应面法和遗传算法相结合对CSP焊点参数进行优化设计是切实可行的。该结论对一些必须同时具备振动可靠性和良好的电气传输性能的电子器件的选用具有一定的指导意义 。
