基于性能的调谐冲击阻尼器优化设计研究
2019-11-20张恒锐吕西林
鲁 正,张恒锐,吕西林
(1.同济大学 土木工程防灾国家重点实验室,上海 200092;2.同济大学 结构工程与防灾研究所,上海 200092)
自从Yao[1]在1972年将结构振动控制技术引入土木工程以来,学者们在控制系统的理论创新和设计方法等方面做了大量的研究,具体工作包括被动控制、主动控制、半主动控制和混合控制。作为一种传统的被动控制技术,调谐质量阻尼器(TMD)因其可靠性被广泛应用于上海中心、台北101大厦等超高层结构[2-3]。然而TMD系统自身有很多缺陷,包括减振频带窄、耐久性差等,因而部分学者将颗粒阻尼技术[4-6]引入到TMD系统并提出一种新的被动控制技术-颗粒调谐质量阻尼器(PTMD)。PTMD系统具备颗粒阻尼和TMD系统各自的优点。在将PTMD应用于土木工程的研究中,Yan等[7-8]开展了附加和不附加调谐颗粒阻尼器的桥梁模型的振动台试验,并基于能量原理提出一种有限元方法来评估阻尼器的减震性能。Lu等[9-10]开展了基于风振benchmark模型的风洞试验以及基于五层钢框架的振动台试验,并提出等效单颗粒的数值模拟方法来评估PTMD系统的减震性能。
然而,之前关于PTMD系统的研究,其参数往往是基于许多假设,并依据实验经验和传统理论来确定。在实际情况下这常常不是最优解。因此为了最大程度减少结构的动力响应,需要提出一个有效且简单的方法来优化设计PTMD系统的参数。另外,之前关于PTMD系统的研究大多基于简单的弹性结构,并没有涉及到复杂的工程应用,例如上海中心,广州塔等。在大震作用下,实际的工程结构往往会进入非线性状态,这就需要通过一些非线性指标来评估PTMD系统的减震性能,例如塑性铰数量和构件塑性耗能。同时,由于PTMD系统存在颗粒之间相互碰撞的高度非线性问题,作为该问题研究的第一阶段,本文忽略PTMD中颗粒之间的碰撞,即认为容器中只有一个钢球,形成调谐冲击阻尼器(TID),来研究该系统在实际工程应用中的优化设计问题。
实际的工程结构往往都有成千上万个自由度,若基于原有限元模型进行TID系统的参数优化设计,必将花费大量的时间成本。在质量阻尼器应用于复杂工程结构方面,Xu等[11]基于广州塔的降阶模型研究了主动质量阻尼器(AMD)系统的风振控制效果。Zhang等[12]基于输电塔的简化模型设计出了TMD系统的最优参数。因而我们也可以通过一个能反映原有限元模型振型参数和动力响应的降阶模型来进行设计研究[13]。基于降阶模型,TID系统的最优参数可以很方便的通过微分演化算法进行设计。本文研究的非线性benchmark模型是美国加州地区一个20层钢结构建筑,它被设计用来评估不同减震装置的减震性能,关于该模型的详细描述可见参考文献[14]。该非线性benchmark结构通过双线性滞回模型来考虑梁柱节点的材料非线性,并采用瑞利阻尼。该benchmark模型前三阶模态频率分别为0.261 Hz,0.753 Hz和1.30 Hz。
本文提出的调谐冲击阻尼器的减振机理的解释包括两方面:① 碰撞过程中颗粒与腔体的动量交换以及该过程中由于两者之间的非完全弹性碰撞造成的能量耗散,即传统冲击阻尼器的减振机理;② 非碰撞时容器腔体与主体结构的调谐以及颗粒冲击对于腔体相位的调整,即调谐质量阻尼器减振机理。本文提出TID系统的基于性能的优化设计方法,具体设计流程见下节。之后将优化设计的TID系统附加到非线性benchmark结构中并评估其减震控制效果。
1 优化设计流程
因为原非线性benchmark有限元模型涉及到大量的自由度,优化设计耗时较大,因而本节根据参数识别原理得到原有限元模型的降阶模型,将原有限元模型缩聚为层剪切模型,可以通过微分演化算法求得,具体过程如下所示
MinimizeJ(z)=[J1(z),J2(k)]
(1)
(2)
(3)
(4)
式中:z=(k1,k2,…,k20,ξ1,ξ2)为识别参数;μk为识别刚度参数的平均值;J1(z)为目标函数响应误差;J2(k)结构刚度的均匀化指标;RMS为均方根响应。识别出的每层刚度参数如表1,前两阶模态阻尼比为0.012和0.014。为了验证降阶模型的有效性,将降阶模型和原有限元模型的振型参数进行比较,结果如图1和图2。
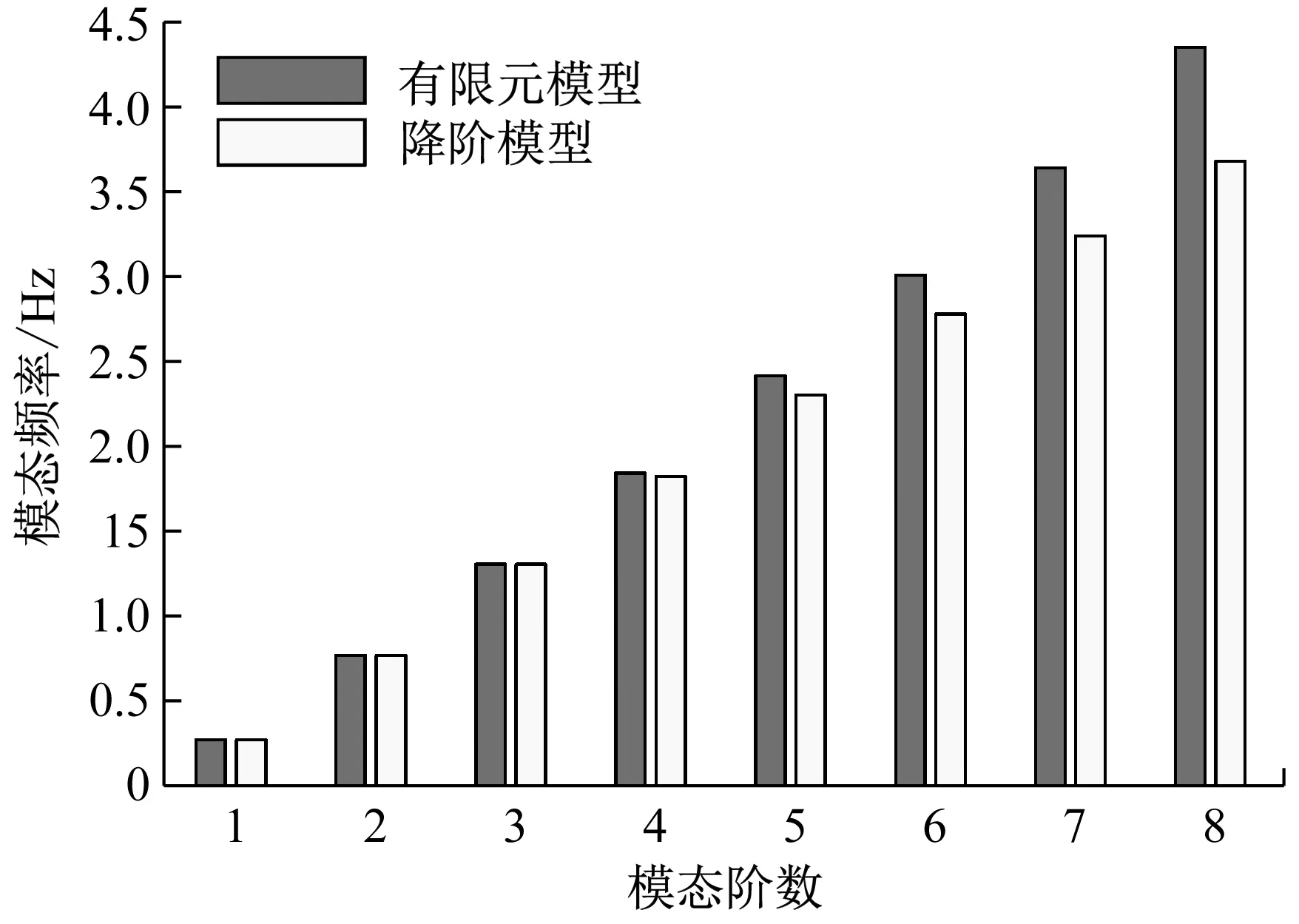
图1 降阶模型和有限元模型振型频率比较Fig.1 Comparison of modal frequency between the original finite element model and reduced-order model
图1和图2表明降阶模型和有限元模型的前四阶振型和模态频率相差不大,误差在可接受的范围内,从而验证了降阶模型的有效性,进而可以采用降阶模型进行TID系统的参数优化设计。将TID系统应用于以上得到的降阶模型,计算简图如图3,系统运动方程如下。
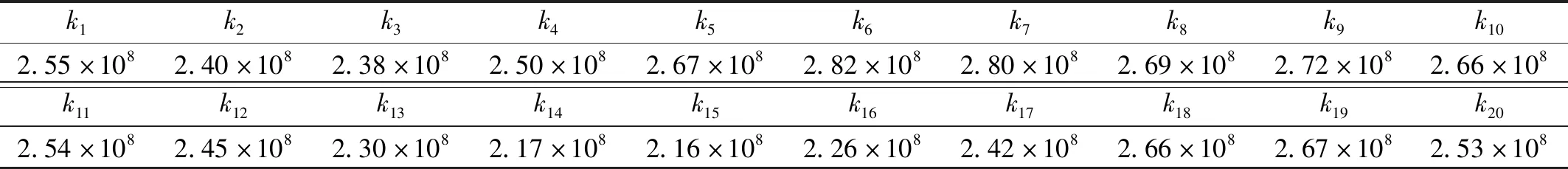
表1 通过微分演化算法识别的刚度参数Tab.1 Stiffness parameters recognition results by Differential Evolution (DE)algorithm N/m

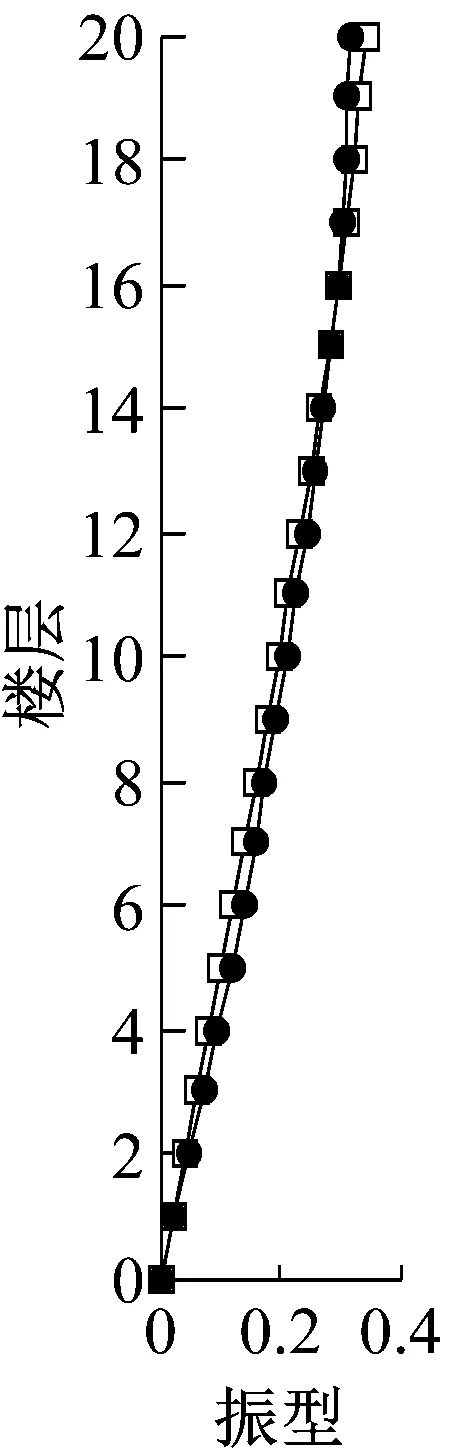
(a)振型1
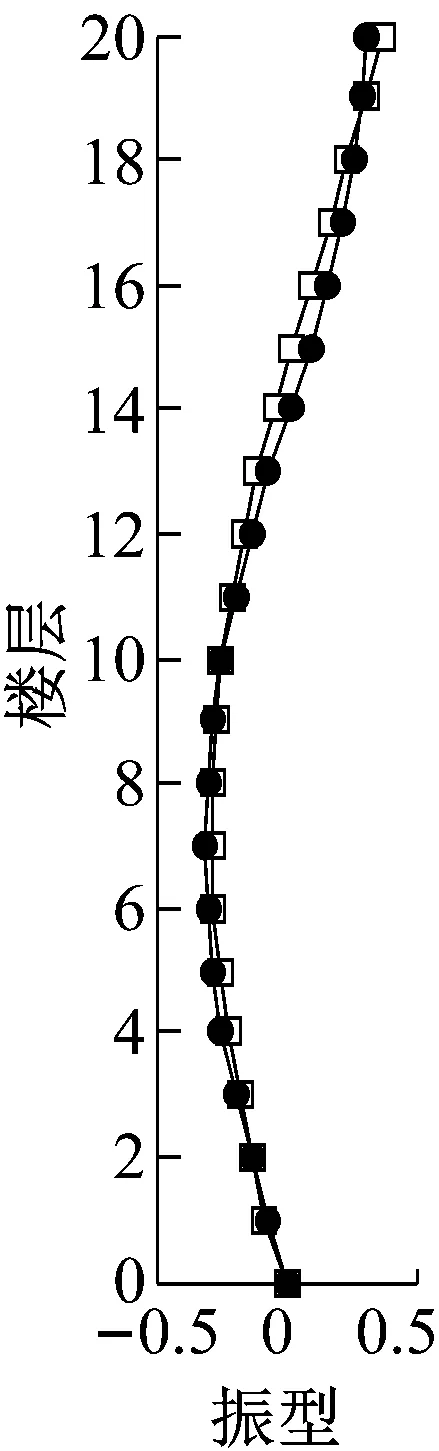
(b)振型2
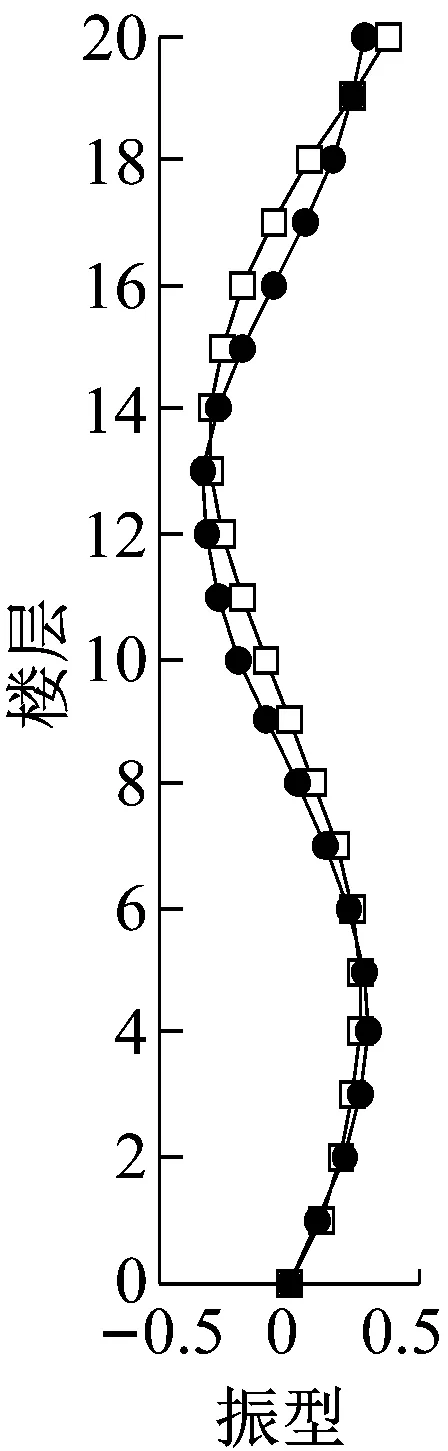
(c)振型3
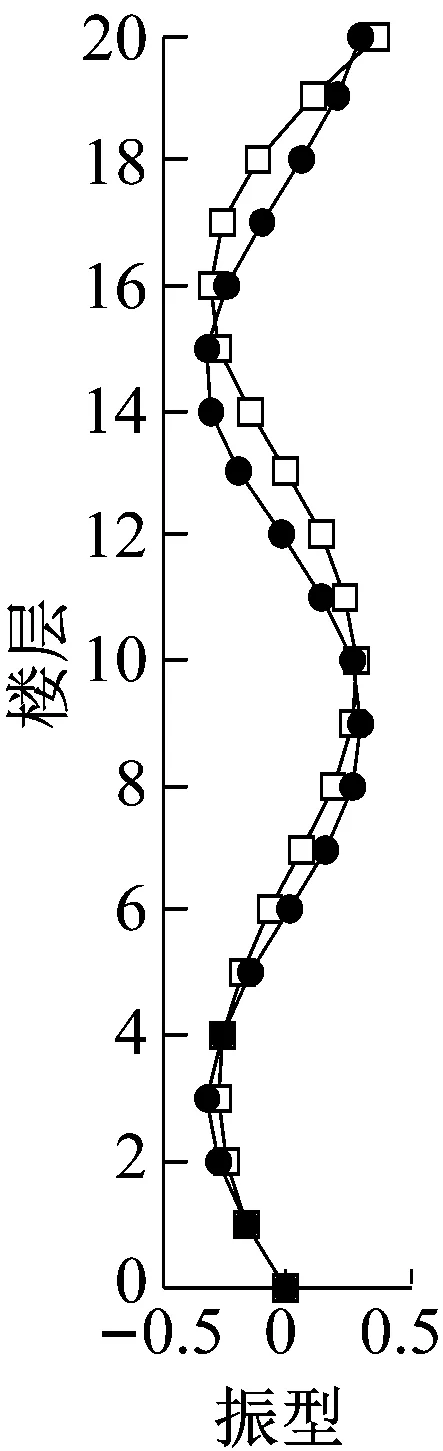
(d)振型4图2 降阶模型和有限元模型振型比较Fig.2 Comparison of the mode shapes between the original finite element model and reduced-order model
(5)

minJ(z)=abs[J1(z)-Jobj]
(6)
(7)
z=(λ,ξ1,ξ2,μ1,μ2,d)
(8)
式中:Jobj=0.60为TID系统目标减振控制效果;J1(z)为主体结构附加优化设计的TID系统的减振效果;d20(t)为无控结构顶层位移响应;d20(z,t)为附加TID系统的结构顶层位移响应;z为TID系统待优化参数向量。

(a)计算简图
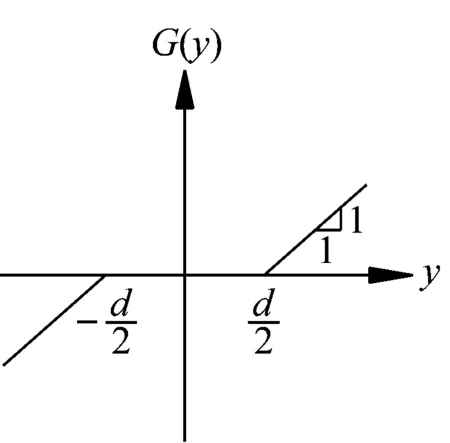
(b)非线性刚度函数
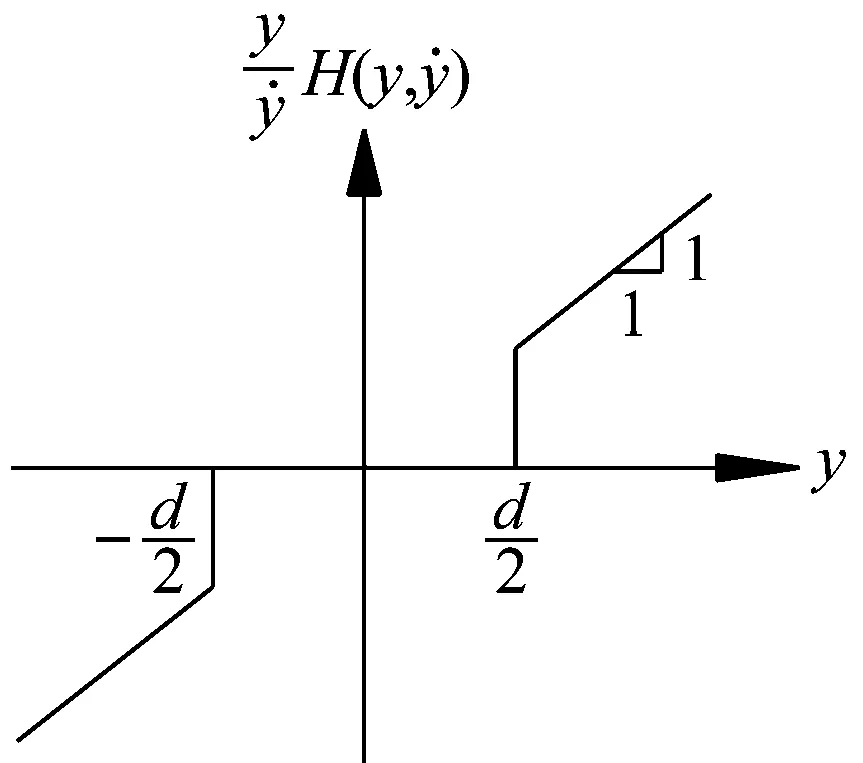
(c)非线性阻尼函数图3 附加TID系统的降阶模型的计算简图和非线性函数Fig.3 Simplified model of the reduced-order model with the TID system and the graph of nonlinear function
2 性能验证
为了进一步验证TID系统优化设计相比传统设计的优越性,本文选取分别经过优化设计和传统设计的TID系统的参数,如表2,然后分别将传统设计和优化设计的TID系统附加到原有限元模型进行减震效果评价分析。
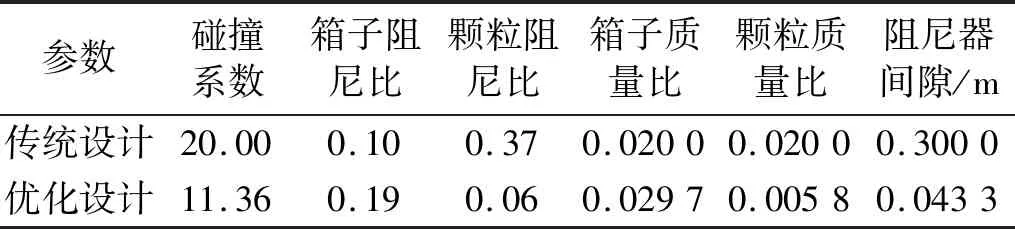
表2 经过传统设计和优化设计的TID系统参数Tab.2 Parameters of the TID system by conventional design and optimal design
图4表示主体结构在幅值系数1.5的El Centro波作用下顶层加速度、位移时程响应和最大层间位移角比较,包括无控结构、传统设计和优化设计。图5表示主体结构在该激励作用下每层峰值和均方根位移,加速度响应比较。图4和图5表明优化后的TID系统可以降低结构的位移响应,包括峰值位移和均方根位移,例如传统设计顶层均方根位移减振率为16.2%,而经过优化设计顶层均方根位移减振率达24%,即优化设计的减振率相比传统设计提高了约50%。然而对加速度响应减震效果不太明显,这是由于针对该特定benchmark结构来说,加速度响应主要由二阶振动模态控制,而位移响应主要是由一阶模态控制[16]。同时图5表明优化后的TID系统可以减少主体结构的层间位移角(尤其对于18层以下),而对于19和20层作用不大,原因可能是颗粒和容器壁以及容器壁与主体结构之间的控制力的特性(主要是碰撞产生控制力),导致了19和20层层间位移角减震效果较差。
考虑到主体结构在大震作用下梁柱节点可能会进入非线性状态,因而有必要评估TID系统对于非线性参数的减震效果,例如塑性铰数量和构件塑性耗能。图6是主体结构在El Centro波作用下的塑性铰数量、构件塑性耗能和塑性铰分布图。其中实心圆点代表无控结构、传统设计和优化设计均有的塑性铰,而空心圆点代表优化设计减少的塑性铰。
图6表明经过优化设计的TID系统可以减少主体结构的塑性铰数量,从无控结构的86个减少到62个。但是对于传统设计,塑性铰的数量不变,只是在楼层的分布发生改变。同时,附加优化设计的TID系统主体结构的构件塑性耗能要小于传统设计,这表明经过优化设计的TID系统可以减少结构在大震作用下的损伤,也进一步验证了本文所提出的基于性能的优化设计方法的优越性。

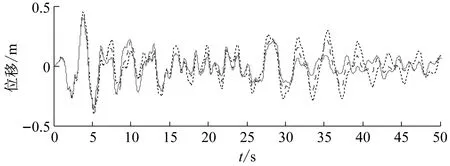
(a)加速度和位移时程
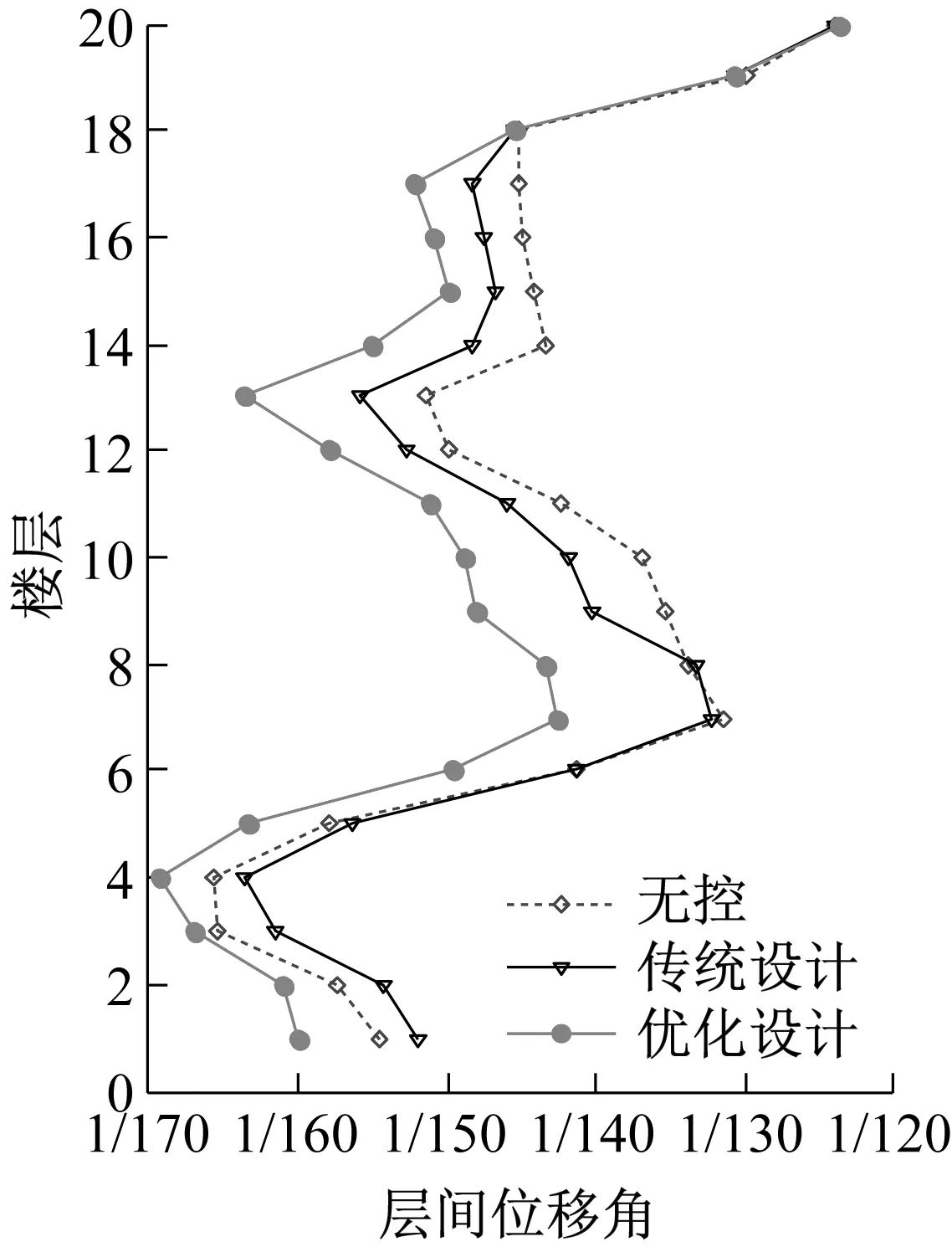
(b)层间位移角图4 主体结构在幅值系数1.5的El Centro波作用下顶层加速度、位移时程和最大层间位移角比较Fig.4 Comparison of the acceleration,displacement time history at the top of the building and inter-story drift ratio between conventional design and optimal design under the action of El Centro wave with scale 1.5


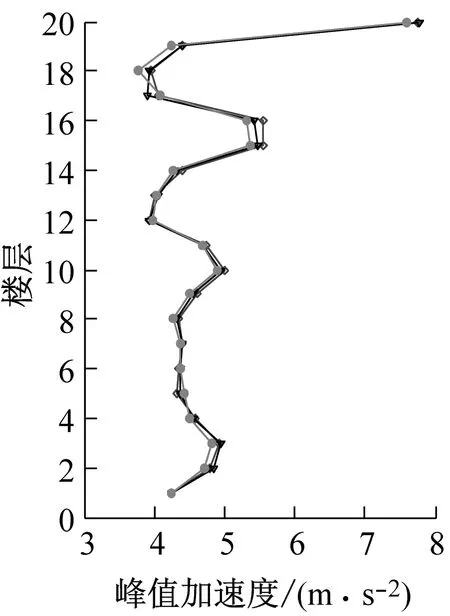
(a)峰值加速度
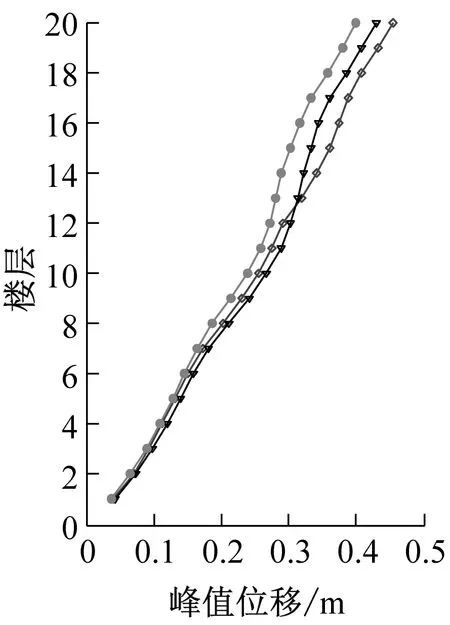
(b)峰值位移
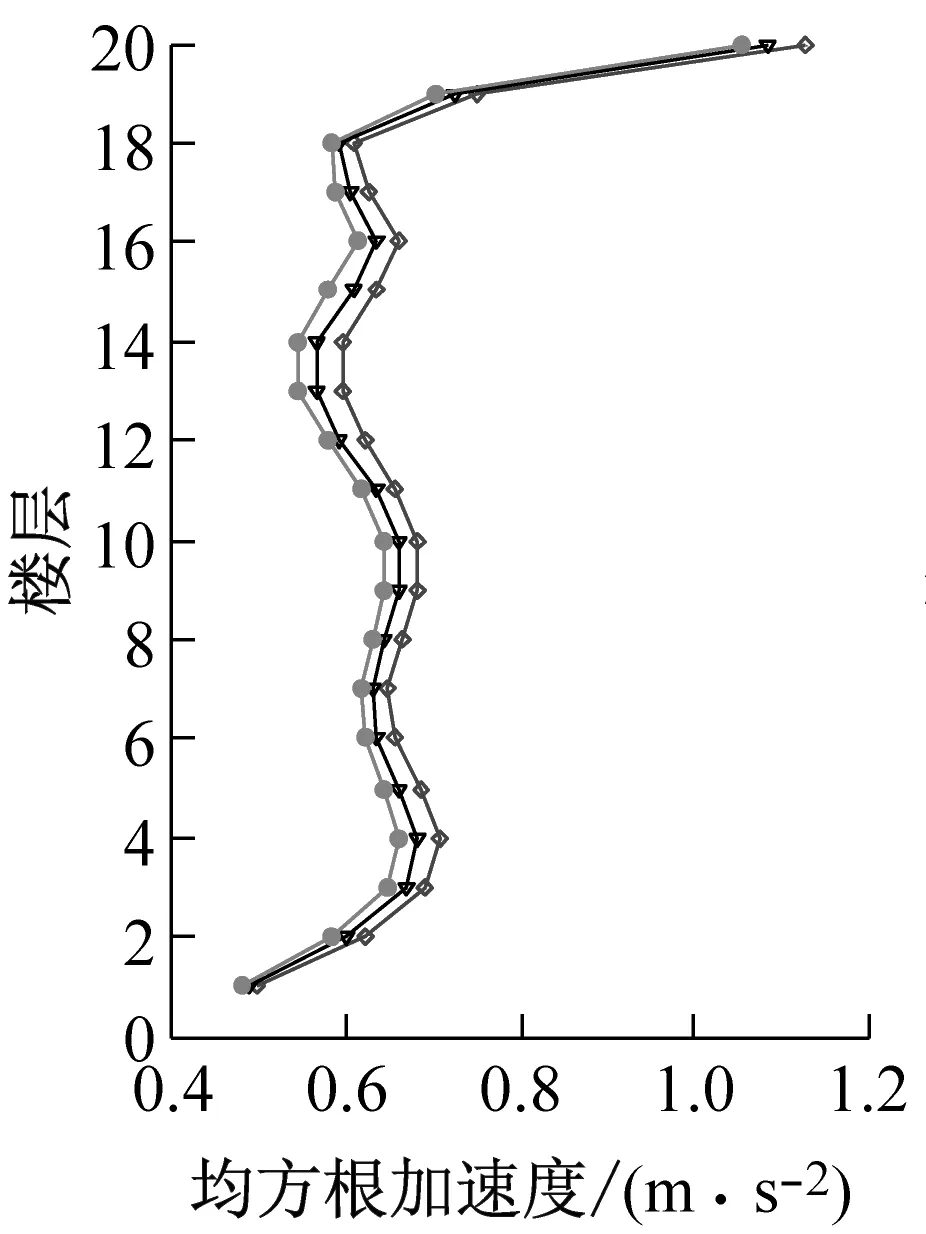
(c)均方根加速度

(d)均方根位移图5 主体结构在幅值系数1.5的El Centro波作用下峰值加速度、位移和均方根加速度、位移比较Fig.5 Comparison of the peak acceleration,displacement response and RMS acceleration,displacement response between conventional design and optimal design under the action of El Centro wave with scale 1.5
3 结 论
本文将一种被动控制装置—调谐冲击阻尼器(TID)系统应用于实际的20层非线性benchmark结构,提出一种基于性能的优化设计方法,基于原有限元模型的降阶模型,设计出TID系统的最优参数,并将其应用于原有限元模型进行性能验证,通过一些指标尤其是非线性指标来验证其相对于传统设计方法的优越性,得出以下结论:
(1)对于大型复杂结构,可以利用降阶模型来设计TID系统的最优参数,这样可以大大减少最优参数设计的时间,缩短结构设计周期。
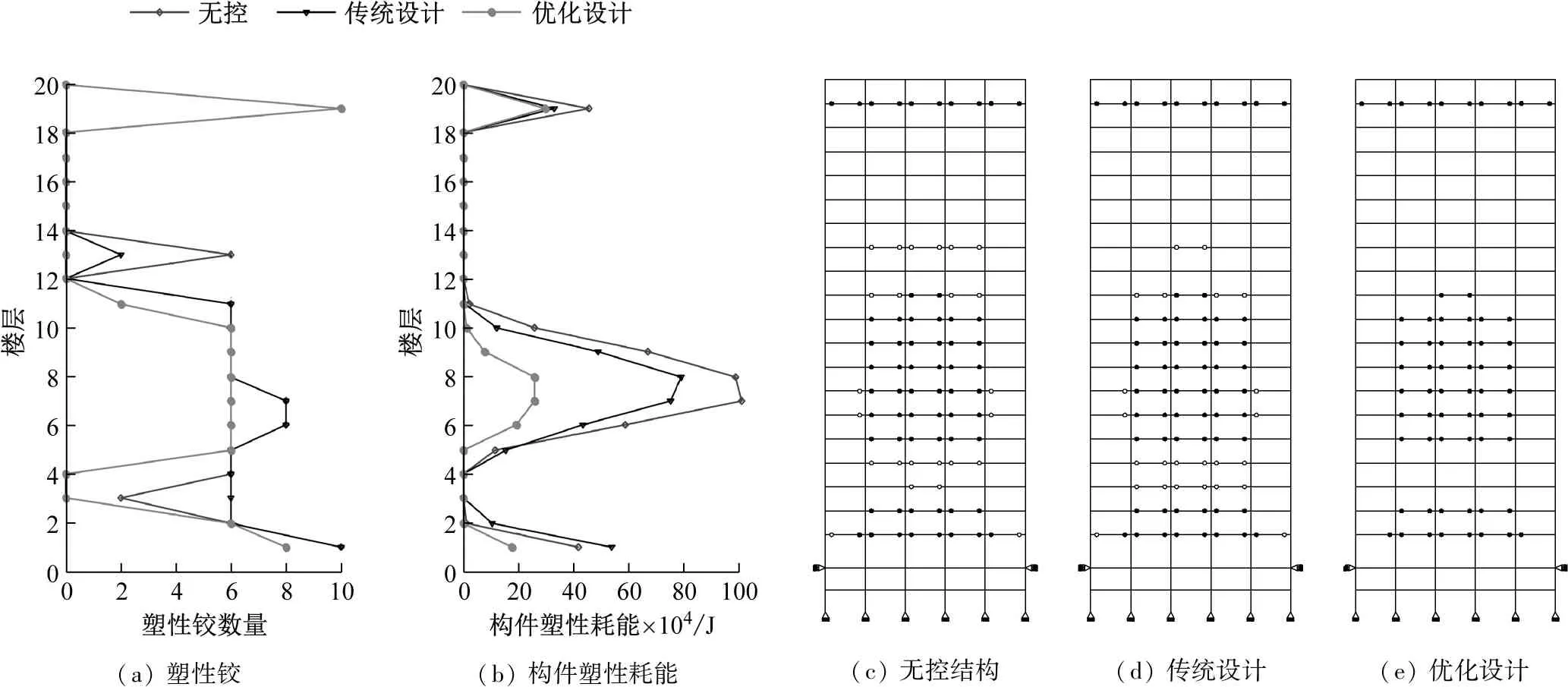
(a)塑性铰 (b)构件塑性耗能(c)无控结构 (d)传统设计 (e)优化设计图6 主体结构在幅值系数1.5的El Centro波作用下塑性铰数量,构件塑性耗能以及塑性铰分布Fig.6 Comparison of the number of plastic hinges,component energy consumption and distribution of plastic hinges between conventional design and optimal design under the action of El Centro wave with scale
(2)降阶模型必须和原有限元模型的动力特性相近,包括振型和模态频率,使两者在动力响应时程上基本吻合,从而验证该降阶模型的有效性。
(3)相对于传统设计的TID系统,经过优化设计的TID系统可以很大程度上减少主体结构的动力响应,包括峰值位移,均方根层间位移角等。
(4)经过优化设计的TID系统可以减少主体结构的非线性响应指标,例如塑性铰数量和构件塑性耗能,因而能减少结构在大震下的塑性损伤。
总之,随着超高层建筑的蓬勃发展,TID系统在减少主体结构地震激励下的动力响应方面必将扮演重要的角色。因此其在土木工程领域具有广阔的应用前景。
