考虑车下设备的城轨车辆弹性车体垂向振动特性研究
2019-11-20郭林生文永蓬尚慧琳宗志祥
郭林生,文永蓬,尚慧琳,宗志祥,孙 倩
(1.上海工程技术大学 城市轨道交通学院,上海 201620;2.上海应用技术大学 机械工程学院,上海 201418)
近年来城市轨道交通的快速发展,随之也产生了一系列如车辆地板异常振动、车辆过弯抖动、车身两端振动剧烈等影响乘客乘坐舒适性的车辆振动问题[1]。车辆在轨道不平顺激励下,由于站间距较短,弯道较多,车辆的行驶速度变化频繁,加之乘客频繁上下站也使车辆的载重频繁的改变,导致车体弹性振动愈加容易被激发,车辆运行平稳性变差,因此城市轨道车辆的弹性振动已经不能被忽略[2]。
车体结构弹性振动对车辆运行平稳性和乘客的乘坐舒适性的影响越来越大[3]。为了改善铁路车辆垂向动力学性能,提高车辆的运行平稳性,近几年在大铁路高速列车上就针对弹性振动问题已开展了大量研究。周劲松等[4]为探究弹性振动对车辆运行平稳性的影响临界问题,通过改变车辆的一阶弹性频率到10 Hz后,车体中部平稳性趋于稳定值,对平稳性影响已经不大。曹辉等[5]考虑共振速度影响车速越高车体对一阶垂弯频率的要求就越大。提高车体自身结构阻尼和一系阻尼,适当降低二系阻尼可以有效的降低车体弹性,提高乘坐舒适度。以上研究都表明车辆的自身结构刚度阻尼的改变会严重影响车体的弹性振动。铁路车辆动力分散式分布导致车下需要悬挂众多设备,而车下设备的悬挂方式以及设备对车辆造成的耦合振动影响也成为研究热点。宫岛等[6]将车体视为两端自由的均质等截面欧拉梁,建立了包含车下设备的两自由度简易弹性车体模型,弹性悬挂的车下设备使整备状态车体的垂向一阶弯曲模态频率得到提升,车体与车下设备模态频率的合理匹配可有效避免二者间共振的发生。Shi等[7]将车下设备考虑成动力吸振器,建立考虑车体弹性的刚柔耦合动力学模型,分析在不同悬挂参数下车体振动和平稳性指标的变化规律,并将仿真结果与台架试验结果进行比较,验证了仿真结果的正确性。罗光兵等[8]考虑将车下设备采用弹性悬挂于车体中部,通过选取合适的刚度和阻尼悬挂参数,车下设备可以有效的降低整车的振动水平。综上,目前主要研究了车体自身结构弹性振动对车辆运行平稳性的影响和改变车下设备悬挂参数来改善振动情况,而对车辆的弹性振动影响因素分析和从全车角度对车体与设备之间的复杂振动关系研究较少。为此,针对城市轨道车辆运行的特点,考虑车体的弹性效应,很有必要明晰城市轨道车辆弹性振动特性和开展车-设备耦合振动相关理论研究。
1 建立含车下设备的弹性车体模型
车体与设备耦合系统垂向动力学模型如图1所示。模型中包含了一个车体,两个构架,四个轮对和一个车下设备。车体的刚体有浮沉和点头两个自由度,两个构架跟车辆刚体自由度一样,有浮沉和点头;车体的运行速度是v,假设车轮与钢轨是全接触的,因此轮对的位移就是轨道不平顺激励输入。文中将车体设定为弹性均质等截面欧拉-伯努利梁。
图1所示车辆模型中,车体总长是L,设定车的垂向振动位移为z(x,t),定义向上为正,其为车体的刚性振动与弹性弯曲振动的叠加,车体的单位长度质量为ρA=Mc/L,ρ为车体密度,A为截面积,E为弹性模量,I为截面惯性矩,μ为内滞阻尼系数;在Z(x,t)中,x为车体上距离其最左端的位置距离,t为时间变量;zc与θc分别表示车体的浮沉和点头运动,zb1、zb2与θb1、θb2为转向架1和转向架2的浮沉与点头运动。文中的车辆参数如表1所示。
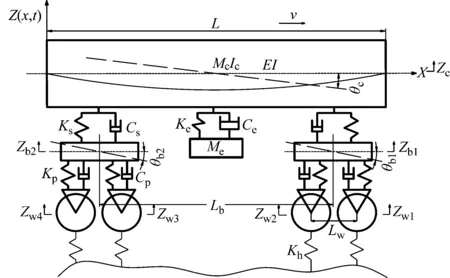
图1 车-设备耦合系统垂向动力学模型Fig.1 The vertical dynamics model of vehicle-equipment coupling system
表1 某城市轨道车辆车-设备耦合动力学模型的参数
Tab.1 Urban rail vehicles-equipment coupled dynamic model parameters
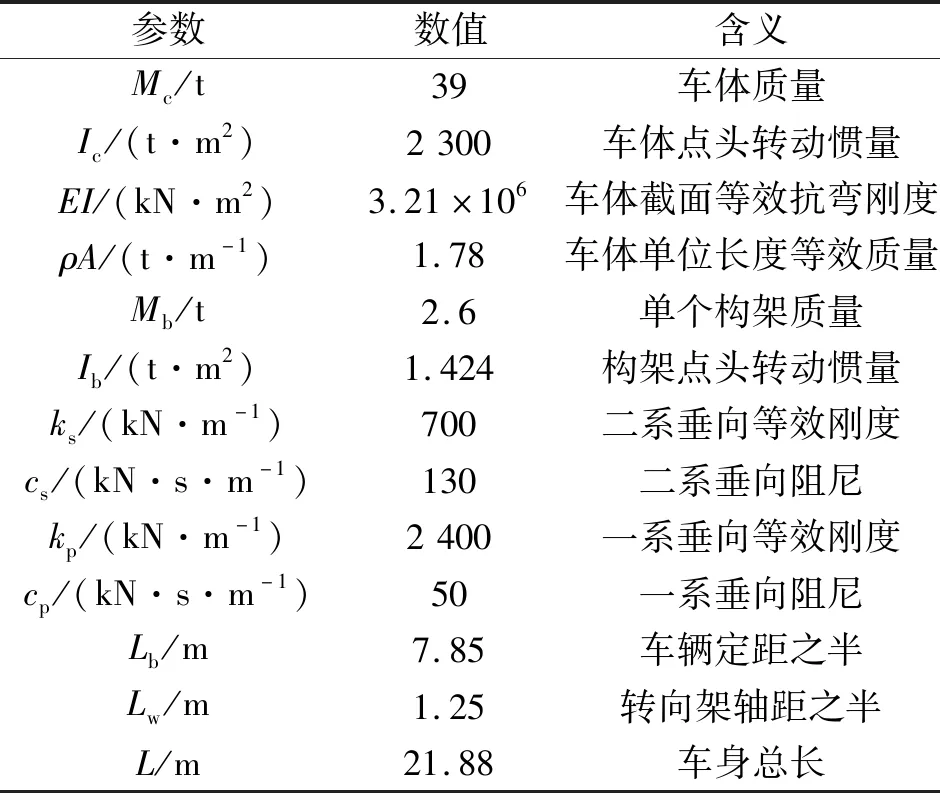
参数数值含义Mc/t39车体质量Ic/(t·m2)2300车体点头转动惯量EI/(kN·m2)3.21×106车体截面等效抗弯刚度ρA/(t·m-1)1.78车体单位长度等效质量Mb/t2.6单个构架质量Ib/(t·m2)1.424构架点头转动惯量ks/(kN·m-1)700二系垂向等效刚度cs/(kN·s·m-1)130二系垂向阻尼kp/(kN·m-1)2400一系垂向等效刚度cp/(kN·s·m-1)50一系垂向阻尼Lb/m7.85车辆定距之半Lw/m1.25转向架轴距之半L/m21.88车身总长
2 模型的求解
根据弹性理论[9-10],图1所示模型车体振动方程为[11-12]
(1)
式中:δ(x)是狄拉克函数;xi是二系悬挂所处位置(i=1,2);Fs1是第一个转向架的二系悬挂作用在弹性车体上的力;Fs2是第二个转向架的二系悬挂作用在弹性车体上的力;Fe是车下设备悬挂处作用在弹性车体上的力。
(2)
(3)
为解式(1)车体振动偏微分方程,先假设车的第i阶振型函数为Yi(x),对应的模态坐标为qi(x)。因为考虑车体的刚性运动,所以把车体的浮沉运动作为第一阶振型,振型函数为Y1(x)=1;车体的点头运动作为第二阶振型,振型函数为Y2(x)=L/2-x;车体的弹性振型从第三阶算起。取n阶模态叠加得到的车体振动位移方程为
(4)
当i≥3时,Yi(x)表示车体的弹性振型,通过应用自由弹性梁的正则振型函数,可以得到应用于本模型的车体振型为
(5)
其中,λi和βi需要满足下列条件
1-chλicosλi=0
(6)
当i=3,4,5…时
λi≈(n+0.5)π(n=1,2,3,4,…)
(7)
βi=λi/L
(8)
将式(4)代入到式(1),再利用式(5)振型函数的正交性,在车的全长上进行积分,结合车的刚性运动方程化简得到车的最终振动方程组为
(9)

(10)
(11)
设备悬挂力Fe为
(12)
而构架和轮对的刚性运动方程可根据以上公式推导可得,在此省略。
车辆系统振动微分方程[13-14]可表示为

(13)
根据式(13)可得到车辆系统的位移频率响应函数和加速度频率响应函数矩阵H(ω),Ha(ω)分别为
H(ω)=(-ω2M+jωC+K)-1F
(14)
Ha(ω)=-ω2H(ω)
(15)
上式频响函数是四输入多输出矩阵,根据车辆轮对时滞特性,可转化为单输入单输出系统如式(16),从而计算出车辆系统各自由度随机振动响应。
(16)
式中,Zw1(ω)作为轮对1的轨道激扰函数;而其中t1=2LW/V,t2=2Lb/V,t3=2(Lw+Lb)/V为其余轮对的时滞。根据弹性车体的振动位移式(4)车体任意点处的加速度响应为
Ha(x,ω)=Hc(ω)+(L/2-x)Hθ(ω)+Hq(ω)
(17)
(18)
3 车体振动响应分析
3.1 车体弹性振动特性分析
将表1的典型城市轨道车辆参数作为计算参数,以垂向美国六级谱为轨道不平顺输入[15]。为了简化计算,刚柔耦合动力学模型中弹性车体仅考虑前两阶弹性弯曲模态。根据表1数据,可算得车辆的弹性一阶和弹性二阶垂弯频率分别为9.85 Hz和27.5 Hz。设定车辆以构造速度80 km/h运行,车体中部以及转向架上方车体振动加速度功率谱如图2所示。

图2 弹性车体的加速度功率谱Fig.2 Acceleration power spectrum of elastic carbody
由图2可知,在刚性主振区,刚性车体和弹性车体的振动几乎是一样的;但在弹性主振区,弹性车体的一阶弹性振动较大,并且在整个车体振动能量中占重要成分,二阶弹性垂弯振动能量很小,可见,车体的弹性振动不可忽略,特别是一阶垂弯振动在弹性振动中占主要部分。
弹性车体的加速度功率谱随着速度变化下的响应如图3所示。由图3可知,车体的刚性振动和弹性振动都随着速度的提高而振动加剧,但在50 km/h速度下,车体的弹性振动明显比60 km/h速度下要大,这是因为轨道不平顺激励谱含有不同频率或者由很多不同的波长组成,当某一波长的激励恰好引发车体某一振型的振动同时与它的自振频率相同,就会产生共振,而此时的速度为共振速度。车体的一阶垂弯频率f1与轨道激励频率(车速与轨道波长之比)相等时,则此时的共振速度为

图3 速度变化对车体弹性振动的影响Fig.3 Influence of velocity change on elastic vibration of carbody
vn=2Lbf1/n(n=1,2,3…)
(19)
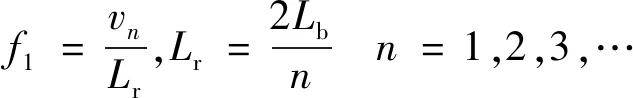
(20)
其中在对应轨道波长下一阶垂弯共振速度在51 km/h附近,所以在50 km/h速度时处在共振速度,一阶垂弯频率处的车体弹性振动明显增加。
载客量变化对弹性车体振动响应的影响如图4所示。由图4可知,载客量的变化对车体振动都是正相关影响。载客量的增加使车体的自重增加,车体越重抑制振动效果越好,随着载客量的增加,对车体振动抑制的效率提高,对于弹性振动的抑制从轻载的9%降幅到超载的45%降幅,刚性振动部分最大能达到63%的抑制效率,载客量的增加相当于车体质量的增加,致使车身刚度发生改变,提高了车体的垂弯频率,从而提高了自身抑制弹性响应的水平。

图4 载客量变化对车体弹性振动的影响Fig.4 Influence of passenger capacity change on elastic vibration of carbody
图5为弹性车体的一阶弹性模态频率由8 Hz增加到11 Hz,随速度变化的车体垂向加速度均方根值。由图5可知,随着速度的提高,车体的弹性振动增大;随着车体的一阶垂弯频率的增加,提高车体的自身刚度,车体的振动情况逐渐好转,而在局部速度下(比如30 km/h、50 km/h和75 km/h附近)车体出现振动突增的现象。这是因为弹性共振速度的存在,不同的弹性一阶模态频率下有多个弹性共振速度,30 km/h、50 km/h和75 km/h附近区域正是车辆的三个共振速度区,在这些速度下导致车体发生振动突增现象。从整体上分析可以得出,车辆在启动、加速过程中,车体的弹性振动会明显增加,随着一阶垂弯频率的提高,车辆的共振速度发生改变,共振峰频率的变化使车体弹性共振降低。
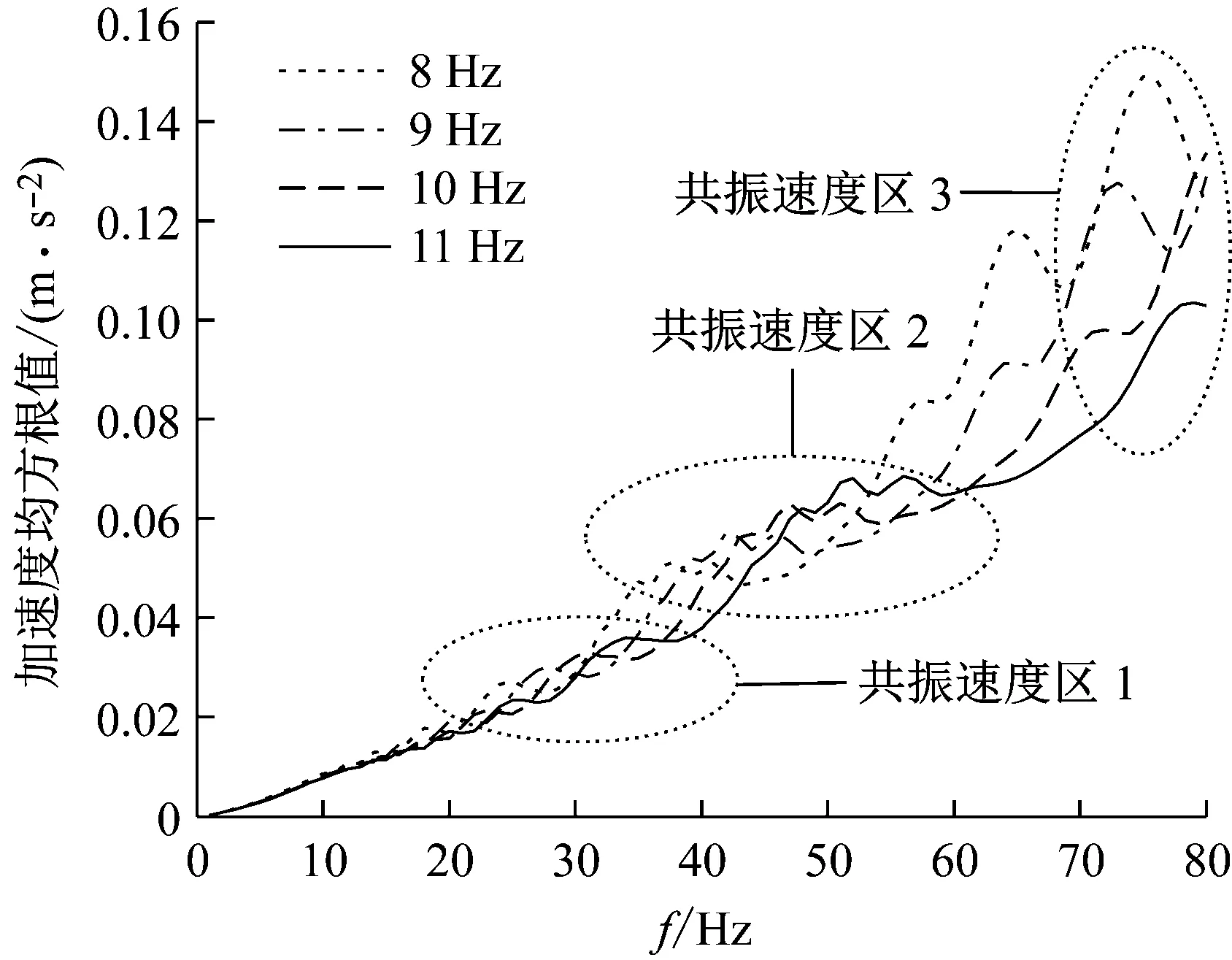
图5 弹性一阶模态频率的改变对弹性车体振动的影响Fig.5 The effect of changing the first-order mode frequency of elasticity on the vibration of carbody
3.2 车-设备耦合振动关系分析
城市轨道车辆车下设备众多,安装位置不同以及设备自身质量也不尽相同,为了分析这些设备对车体的振动产生的影响,仿真分析中,通过改变车下设备的安装位置和改变设备的质量来研究弹性车体与设备之间的耦合振动关系并为城市轨道车辆车下设备布局提供指导。
若将设备安装在车体中部位置,弹性车体无设备、设备采用刚性悬挂和采用弹性悬挂时车体中部与转向架上方振动加速度功率谱响应,如图6所示。
由图6(a)可知,车体中部振动能量主要来自于车体的弹性振动;相比无设备情况而言,设备分别采用刚性悬挂与弹性悬挂这两种悬挂方式,对车体1 Hz附近的刚性浮沉运动有几乎相同的振动抑制效果;而在10 Hz附近弹性振动处,弹性悬挂对车体弹性振动的抑制效果明显优于刚性悬挂,但是在弹性振动一阶振动频率左侧出现较大峰值,使峰值频率偏移,即设备的弹性悬挂使车体发生“频率跳变”现象[16],而刚性悬挂的车体几乎没有发生频率偏移现象。这是因为设备改为弹性悬挂,设备悬挂频率的改变使车体的一阶弹性弯曲频率发生改变,引起设备-车体耦合共振,低阶模态发生同向共振[17],高阶模态发生反向共振。由图6(b)可知,转向架上方车体的弹性振动能量减弱,而此时车体的振动能量主要来自于车体的浮沉和点头两种垂向刚性运动。
由图6综合分析可知,车体的弹性振动由中部向两侧衰减,转向架处的点头影响使车体的刚性振动加大。设备的弹性悬挂会使车体的弹性一阶峰值频率发生偏移,但弹性悬挂仍可以有效的抑制车体的弹性振动,同时在设备的悬挂频率的设计上应多考虑反向共振对振动的抑制作用。
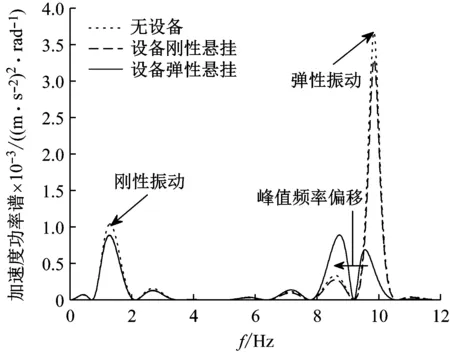
(a)车体中部
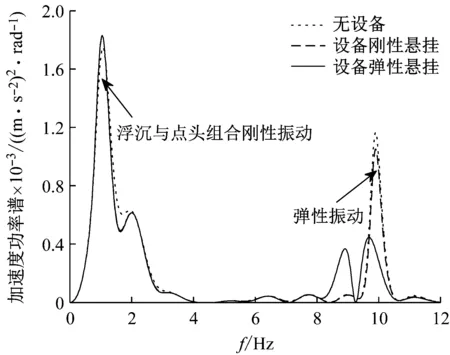
(b)转向架上方图6 设备悬挂方式对车体振动影响Fig.6 Effects of equipment suspension on the vibration of carbody
当设备重固定为3.9 t时,调整该设备的安装位置,考察车体的其他位置的加速度功率谱峰值变化,如图7所示。由图7可知,设备安装在车体中部时,车体所有位置弹性振动峰值较小,说明对车体所有位置的弹性振动的抑制效果很好,这就是尽量将设备布置在车体的中部的原因;设备安装在一端位置时,所在端的弹性振动峰值较小,说明对车体的弹性振动的抑制效果较好,但造成车体另一端增振,类似“跷板”现象,这就是说,设备尽量要放在中部,考虑车体中间位置空间的有限性,务必对称布置;设备安装在转向架附近处时,对车体全车位置处的振动影响都较小,该处自身的弹性振动也比较小,因此转向架处适合放置对振动敏感的设备。
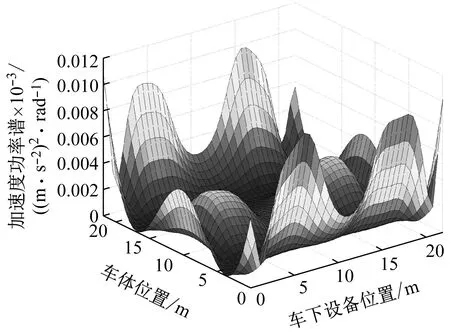
图7 设备安装位置对车体不同位置弹性振动峰值影响Fig.7 Influence of equipment installation position on peak value of elastic vibration at different positions of vehicle body
当设备安装在车体中部时,不同质量的车下设备对车体不同位置处的弹性振动加速度功率谱峰值的影响如图8所示。由图8可知,随着设备质量的增大,反映车体弹性振动大小的加速度功率谱峰值先增大后减小,然后又逐渐增大。0.5 t左右重的设备对车体有较大增振的效果,而4.5 t左右重能够最大程度的抑制车体的弹性振动,当重量超过5吨左右时对车体又造成增振,这是因为设备与车体会发生耦合共振,设备自身的振动频率与车体弹性振动频率远离,则弹性振动抑制不明显,所以,质量低于1 t左右和超过5 t左右的设备抑制振动效果不好,不建议采用弹性悬挂方式。车下设备除了在所在安装位置处发生耦合振动关系,对车体的其他位置处也产生耦合振动影响,在Ⅰ位端和Ⅱ位端转向架附近有最小的弹性振动,因此,其他设备比如高精度的检测设备建议就安装在转向架附近处,能够降低车体弹性振动的影响,并且减少中部设备对其他设备的干扰。

图8 设备质量改变对车体不同位置弹性振动峰值影响Fig.8 Influence of equipment quality change on peak vibration amplitude of different positions of vehicle body
3.3 车体全车振动变化特性分析
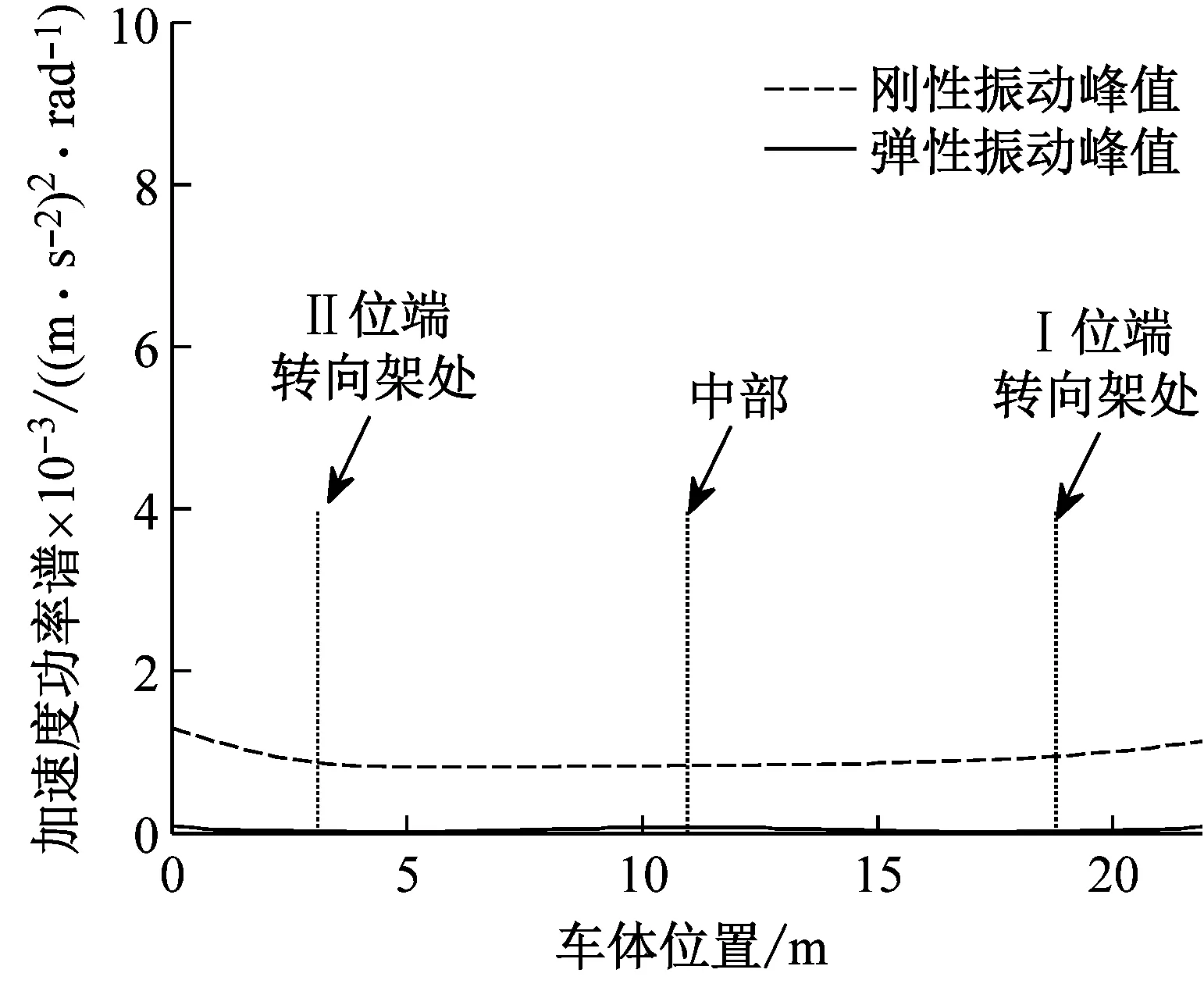
基于城市轨道交通乘客乘坐特殊性,车辆全车的乘客站与站之间动态流动,图9是四个典型速度下车体在全车不同位置处的刚性振动和弹性振动峰值变化情况。
由图9可知,全车刚性振动变化较为平缓,在转向架处刚性振动存在极小值,全车刚性并非以车体中部位置对称,这是因为轨道不平顺对各个轮对的存在时滞影响,这种影响造成车体前部和后部存在略微不对称。全车弹性振动变化比较剧烈,在构造速度80 km/h车速运行下尤其如此,在车体中部和端部出现较大峰值,在转向架附近处的弹性振动非常小,车体全车弹性振动变化呈现一个略微不对称的“W”变化特征,这是因为弹性一阶振型对车体的弹性振动贡献最大,所以在车体中部会出现较大垂弯,而转向架起到车体弹性弯曲支点作用,因此在转向架附近处弹性振动非常小,并导致车体的两端弹性振动恶化。在60 km/h车速运行下,全车弹性振动非常低,这是因为50 km/h和70 km/h附近是弹性共振速度,60 km/h是介于弹性共振速度之间的非共振速度,在非共振速度下运行,能够有效降低车体的弹性共振,提高乘客的乘坐舒适性。

(a)50 km/h
(b)60 km/h

(c)70 km/h
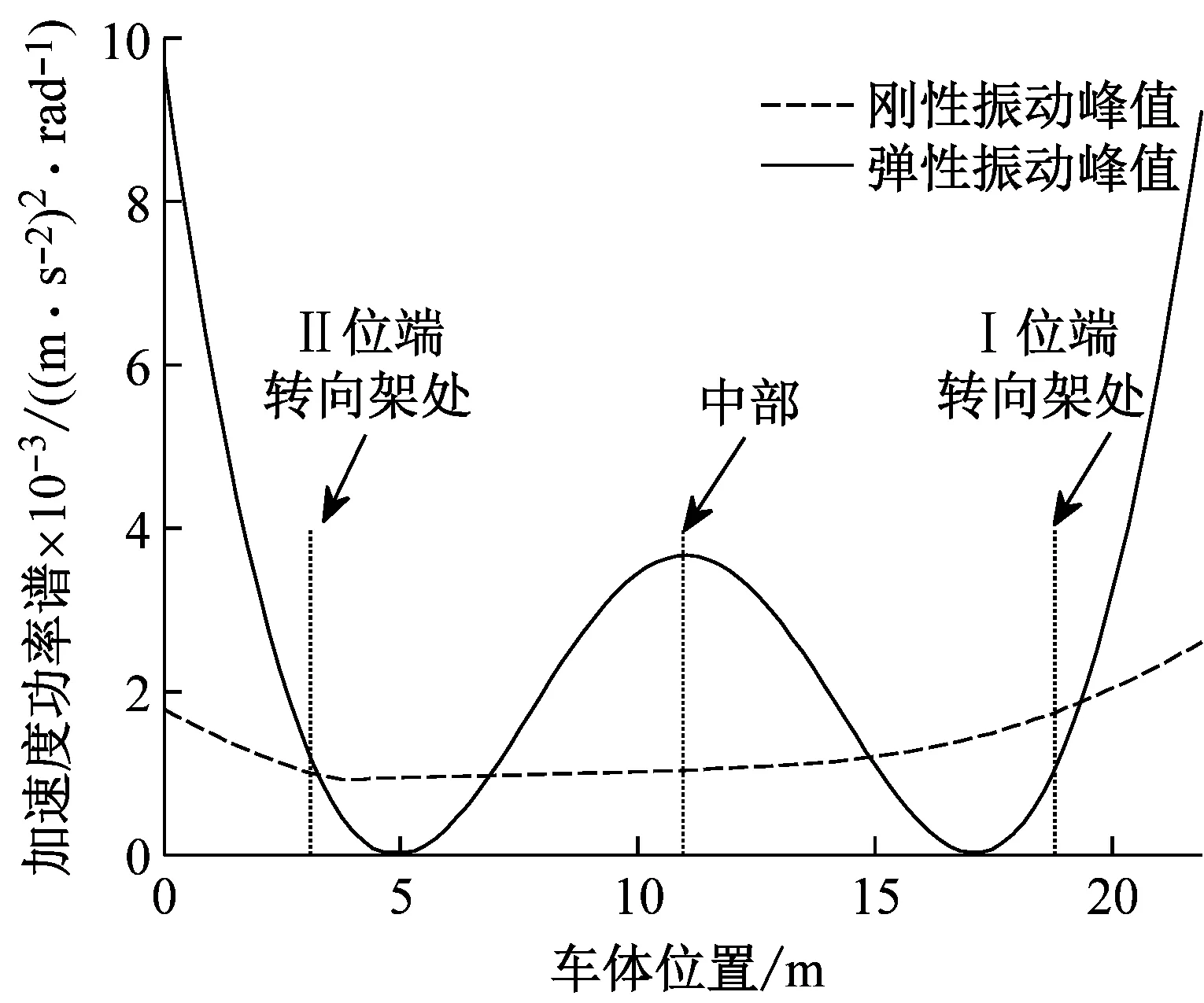
(d)80 km/h图9 车体振动峰值变化情况Fig.9 The carbody’s vibration peak changes
4 弹性车体平稳性评价
城市轨道车辆的振动情况与乘客的乘坐舒适度的关系可以通过Sperling平稳性指标来评价。
图10是在不同速度下的弹性车体与刚性车体的典型位置处垂向Sperling平稳性变化情况。由图10可知,随着车辆运行速度的提高,来自轨道不平顺的激励能量就越大,弹性车体和刚性车体的运行平稳性都随着速度的提高而变差。在弹性共振速度的影响下弹性车体的弹性振动增大,车体的垂向Sperling指标变大,运行平稳性变差,所以考虑车体弹性的城市轨道车辆在运行时尽量要避开弹性共振速度,较少它对车辆运行平稳性的影响,提高乘客乘坐舒适度,车体的中部相较于车体两端平稳性更好。
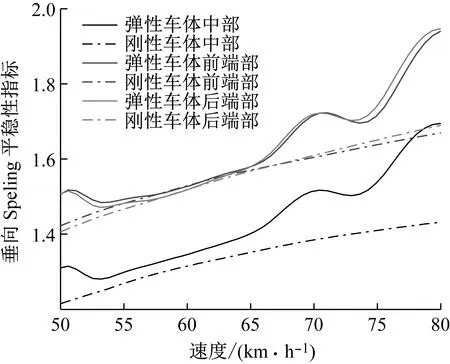
图10 车体典型位置处的sperling指标Fig.10 Sperling index at the typical location of the carbody
5 结 论
(1)城市轨道车辆的运行速度和载客量的改变对车体的弹性振动有重要影响,因此城市轨道车辆考虑车体的弹性效应很有必要,当车下设备采用弹性悬挂,对弹性车体的全车振动有很好的抑制作用。
(2)车下设备对称布置在车体中部,可以最大限度的抑制车体全车振动,并且能够有效避免车体的“跷板”现象;转向架附近处振动最小,建议布置对振动敏感设备;设备质量与车体全车振动并非呈单调变化,设备4.5 t左右重能够最大程度的抑制车体的弹性振动,而质量低于1 t左右和超过5 t左右的设备抑制振动效果不好,则不建议采用弹性悬挂,因此,从抑制车体全车振动的角度,对不同质量的车下设备采用的悬挂方式选择要谨慎。
(3)车体全车的弹性振动呈现一个略微不对称的“W”状变化特征,受一阶垂弯影响,车体中部有较大峰值,转向架作为振动支点振动最小,两端振动最大。对比刚性振动,车体弹性振动受共振速度影响较大,在非共振速度下运行,能够有效降低全车的弹性共振,提高乘客的乘坐舒适性。
