一般混合变分不等式的新间隙函数

赖学李, 夏福全

(四川师范大学 数学科学学院, 四川 成都 610066)

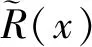
1 预备知识

本文在n维欧式空间Rn中研究一般混合变分不等式问题,且在该空间的范数和内积分别表示为‖·‖和〈·〉.

定义 1.1设S是Rn上的非空闭凸集,F:Rn→Rn是一个映射,f:Rn→(-∞,+∞]是真凸下半连续泛函,而domf={x∈Rn:f(x)<+∞}为f的有效域,且S⊆domf,则一般混合变分不等式问题(简记为MVIP(F,S))为:求x*∈S使得

〈F(x*),x-x*〉+f(x)-f(x*)≥0,

∀x∈S,

(1)

若此时f是闭凸集S上的指示函数,即

则一般混合变分不等式(1)退化为下列的经典变分不等式问题,简记为VIP(F,S):求x*∈S使得

〈F(x*),x-x*〉≥0, ∀x∈S.

(2)

在利用变分不等式问题的间隙函数,将变分不等式问题转化为特殊的凸优化问题进行研究,已经得到了许多广泛而深入的研究成果.比如:Auslender[1]首先定义了问题(2)的间隙函数

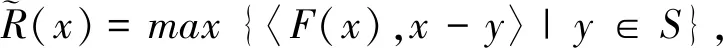
(3)

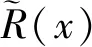
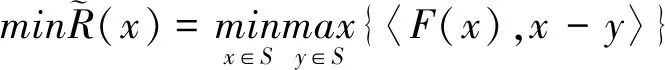
与问题(2)等价.

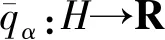
(4)

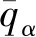
Taji等[3]此时在(4)式的基础上取α=1,此时这个正则间隙函数变成了

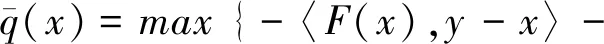
(5)

以下是来自文献[8]的一些与本文有关的定义和结论.

定义 1.2称函数f:Rn→(-∞,+∞]为:

1) 凸函数,若∀x,y∈domf,α∈(0,1)使得不等式

f((1-α)x+αy)≤(1-α)f(x)+αf(y);

2) 严格凸函数,若∀x,y∈domf,α∈(0,1)使得不等式

f((1-α)x+αy)<(1-α)f(x)+αf(y);

3) 强凸函数,若∀x,y∈domf,α∈[0,1]，存在σ>0,使得不等式

f((1-α)x+αy)<(1-α)f(x)+αf(y)-

定义 1.3正常凸函数f:Rn→(-∞,+∞]在点x∈domf处沿方向d的方向导数记为

(6)

定义 1.4称向量ξ为凸函数f在点x处的次梯度,即当ξ∈Rn使得对任意的y∈Rn,均有

f(y)-f(x)≥〈ξ,y-x〉,

(7)

其中全体ξ的集合称为f在点x处的次微分,记作∂f(x).

引理 1.5设函数f:Rn→(-∞,+∞],其中domf为开凸集,若f在domf上可微,则在f为(严格)凸函数的充要条件即为∀x,y∈domf,x≠y有

f(y)-f(x)≥q(>)〈▽f(x),y-x〉.

(8)

引理 1.6正常凸函数f:Rn→(-∞,+∞]以及x∈domf,则ξ∈∂f(x)的充要条件是

f′(x;d)≥〈ξ,d〉,d∈Rn.

(9)

2 新的间隙函数

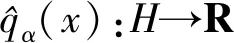
(10)

其中φ(x,y):Rn×Rn→R满足以下条件:

(A1)φ在Rn×Rn上连续;

(A2)φ在Rn×Rn上非负且φ(x,y)=0当且仅当x=y;

(A3)φ(x,·)关于x也是强凸的,也即存在η>0,对任意的x∈Rn满足

φ(x,y1)-φ(x,y2)≥〈▽yφ(x,y2),y1-y2〉+

η‖y1-y2‖2, ∀y1,y2∈Rn,

其中▽yφ表示φ关于第二变量的偏导数;

(A4) ▽yφ(x,·)是Rn具有模μ≥2η的一致Lipschtz连续函数,即存在大于零的常数μ≥2η,使得对任意的x∈Rn有

‖▽yφ(x,y1)-▽yφ(x,y2)‖≤

μ‖y1-y2‖, ∀y1,y2∈Rn;

(A5) 对任意的x,y∈Rn,▽xφ(x,y)=-▽yφ(x,y).

此时,若φ(x,y)=〈y-x,G(y-x)〉,可知φ(x,y)满足(A1)⟹(A5),再取α=1,(10)式变形为

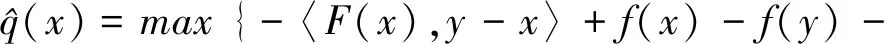
(11)

在本文中,假设集合S满足

S={x∈Rn:gi(x)≤0,

i=1,2,…,m},

(12)

其中gi:Rn→R是二阶连续可微的凸函数,并且Slater约束规范成立,即存在x0∈Rn,满足

gi(x0)<0,i=1,2,…,m.

(13)

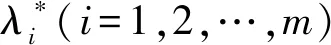
i=1,2,…,m.

(14)

证明对于给定的

S={x∈Rn|gi(x)≤0,i=1,2,…,m},

若x*∈S是MVIP(F,S)的解,那么存在ξ(x*)∈∂f(x*)满足

-F(x*)-ξ(x*)∈Ns(x*).

又由于Cs(x*)⊆coTs(x*)(其中Ns(x*)、Cs(x*)、Ts(x*)分别表示集合S在x*处的法锥、线性化锥、切锥)，从而根据文献[8]的性质2.12有

Ns(x*)=Ts(x*)*=

(coTs(x*))*⊆Cs(x*)*,

那么

-F(x*)-ξ(x*)∈Cs(x*)*,

而由于

Cs(x*)={y∈Rn|〈▽gi(x*),y〉≤0,

i∈I(x*)},

其中I(x*)={i|gi(x*)=0}⊆{1,2,…,m}.

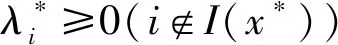
i=1,2,…,m.

证毕.

若S是一般的非空闭凸集,则(5)式所定义的间隙函数赋值非常困难.因此,Taji等[3]定义了一个新的多面体代替了(5)式中的集合S,其形式为

M(x)={y∈Rn|gi(x)+

〈▽gi(x),y-x〉≤0,i=1,2,…,m}.

(15)

相应地,Taji等[3]定义了问题(2)的新的间隙函数

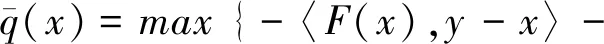
显然，由于M(x)是一个凸多面集,该新的间隙函数赋值非常容易.首先证明M(x)所具有的一个性质.

定理 2.2设M(x)是由(15)式所定义的集合,则M(x)是一个包含(5)式中集合S的一个凸多面集.

证明任取y∈S⊆Rn,从而根据(10)式得gi(y)≤0,i=1,2,…,m.由于gi(x),i=1,2,…,m,是一列二阶连续可微的凸函数,从而根据引理1.6,对∀x∈Rn有

gi(y)-gi(x)≥〈▽gi(x),y-x〉,

i=1,2,…,m,

从而有

gi(x)+〈▽gi(x),y-x〉≤gi(y)≤0,

i=1,2,…,m.

故y∈M(x),即S⊆M(x).证毕.

受到文献[3]思想的启发,也将(11)式中的S替换为凸多面体M(x),重新定义下列函数:

q(x)=max{-〈F(x),y-x〉+f(x)-f(y)-

(16)

对给定的x∈S,令

Q(y)=〈F(x),y-x〉-f(x)+f(y)+

定理 2.3设函数Q(y)由上式所定义,以及M(x)是由(15)式所定义的凸多面集,那么函数Q(y)具有唯一的最大值.

证明对给定的x∈S,令

Q(y)=〈F(x),y-x〉-f(x)+f(y)+

若要证明函数Q(y)具有唯一的最大值,只需要证明-Q(y)具有唯一的最小值,从而只需要证明-Q(y)是一个强凸函数即可.然而这是显然的.因为〈F(x),y-x〉关于y是线性函数,f是真凸下半连续泛函，从而混合项部分f(y)-f(x)是凸的;而G-范数〈y-x,G(y-x)〉/2强凸的,故-Q(y)是强凸的,从而根据引理1.7可得Q(y)具有唯一的最小值.证毕.

根据定理2.3,设L(x)是关于y的一个二次规划问题:

〈F(x),y-x〉+f(y)-f(x),

s.t.y∈M(x)

(17)

的唯一最大解.此时(16)式即

q(x)=-〈F(x),L(x)-x〉+f(x)-f(L(x))-

(18)

对给定的x∈S,设

N(y)=〈F(x),y-x〉+f(y)-f(x)+

(19)

令指示函数

且设

J(y)N(y)+δM(x)(y),

(20)

若y*∈M(x)是(16)式的解,此时根据(17)式的最优性条件有

0∈∂J(y*)=∂N(y*)+∂δM(x)(y*),

(21)

由于

∂N(y*)=∂(〈F(x),y-x〉+

F(x)+∂f(y*)+G(y*-x).

所以,对任意的y∈M(x)有

(f+δM(x))(y)-(f+δM(x))(y*)≥

-〈y-y*,F(x)+G(y*-x)〉,

(22)

即

f(y)-(f+δM(x))(y*)≥

-〈y-y*,F(x)+G(y*-x)〉,

(23)

此时令y*=L(x)∈M(x),则得到变分不等式

〈F(x)+G(L(x)-x),y-L(x)〉+

f(y)-f(L(x))≥0, ∀y∈M(x).

(24)

定理 2.4设x∈Rn,F:Rn→Rn是一连续映射,f:Rn→(-∞,+∞]是一真凸下半连续泛函,且x∈S⊆domf,则以下结论等价:

(a)x是(1)式的解;

(b) -F(x)∈∂(f+δM(x))(x);

(c)L(x)=x.

证明(a)⟹(b) 假设x∈S是一般混合变分不等式MVIP(F,S)的解,则对任意的y∈S有

〈F(x),y-x〉+f(y)-f(x)≥0,

(25)

由于S⊂M(x),从而

〈F(x),y-x〉+(f+δM(x))(y)-

(f+δM(x))(x)≥0, ∀y∈Rn,

(26)

即对任意的y∈Rn得

(f+δM(x))(y)-(f+δM(x))(x)≥

〈-F(x),y-x〉,

(27)

从而

-F(x)∈∂(f+δM(x))(x).

(b)⟹(c) 假设-F(x)∈∂(f+δM(x))(x),那么0∈F(x)+∂(f+δM(x))(x),则对任意的y∈M(x),

f(y)-f(x)≥〈-F(x),y-x〉.

在上式中令y=L(x)∈M(x),则

f(L(x))-f(x)≥〈-F(x),L(x)-x〉.

由于x∈S⊂M(x),在(24)式中取y=x有

〈F(x)+G(L(x)-x),x-L(x)〉+

f(x)-f(L(x))≥0.

根据上述两式可得

〈G(L(x)-x),L(x)-x〉≤0.

再由G是对称正定矩阵可知L(x)=x.

(c)⟹(a) 假设L(x)=x,根据(24)式显然有

〈F(x),y-x〉+f(y)-f(x)≥0,

∀y∈M(x),

(28)

因为S⊆M(x),为了要证明x=L(x)∈M(x)是一般混合变分不等式MVIP(F,S)的解,只需要证明x∈S即可.事实上,由于x=L(x)=ymax∈M(x),根据(15)式给定的M(x)的定义,

gi(x)+〈▽gi(x),L(x)-x〉≤0,

i=1,2,…,m.

(29)

所以gi(x)=gi(L(x))≤0,所以x∈S,即x是MVIP(F,S)的解.证毕.

接下来,考虑优化问题

minq(x),

s.t.x∈S,

(30)

其中函数q是由(16)式所定义的.接下来的定理建立了一个关于MVIP(F,S)和优化问题(30)之间的等价关系.

定理 2.5令q:Rn→R是由(16)式所定义的函数,则对任意的x∈S,都有q(x)≥0.此外x∈S以及q(x)=0当且仅当x是MVIP(F,S)的解.因此x∈S是MVIP(F,S)的解当且仅当它是优化问题(30)的解并且q(x)=0.

证明由x∈S⊆M(x),那么根据定理2.3以及(16)式有

q(x)≥-〈F(x),x-x〉+f(x)-f(x)-

(31)

根据定理2.4得到x∈S是MVIP(F,S)的解当且仅当L(x)=x,故只需证明x∈S以及q(x)=0当且仅当L(x)=x.

必要性 首先,假设x∈S以及q(x)=0,由于x∈M(x),由(24)式有

〈F(x)+G(L(x)-x),x-L(x)〉+

f(x)-f(L(x))≥0,

从而有

-〈F(x),L(x)-x〉+f(x)-f(L(x))≥

〈L(x)-x,G(L(x)-x)〉,

(32)

不等式的两边同时减去

那么有

-〈F(x),L(x)-x〉+f(x)-f(L(x))-

而由于(18)式

q(x)=-〈F(x),L(x)-x〉+f(x)-f(L(x))-

从而

(33)

但由于G-范数正定且q(x)=0,则有L(x)=x.

充分性 反过来,假设L(x)=x,则根据(18)式,从而有q(x)=0.此外通过二次规划问题(17)可知

gi(x)+〈▽gi(x),L(x)-x〉≤0,

i=1,2,…,m,

那么有L(x)=x满足x∈S,从而有q(x)=0的x就是优化问题(31)的最优解.证毕.

3 q的连续性和可微性

定义 3.1[3]令φ:K→2K是一个集值映射,K是Rn中的一非空子集.

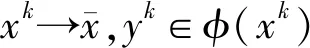
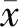
命题 3.2令gi:Rn→R(i=1,2,…,m)是连续可微的且满足Slater约束规范成立,则由(15)式所定义的点集映射M在Rn上是连续映射.

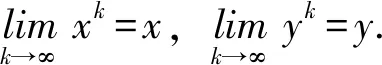
gi(xk)+〈▽gi(xk),yk-xk〉≤0,

故

gi(x)+〈▽gi(x),y-x〉≤0,

从而

y∈M(x).

所以M(x)在每一个x处都是闭映射.

另一方面,根据凸函数的性质有

gi(y)-gi(x)≥〈▽gi(x),y-x〉,

那么有

gi(x)+〈▽gi(x),y-x〉≤gi(y)≤0,

从而

y∈M(x).

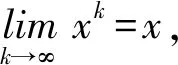
gi(x)+〈▽gi(x),y-x〉,

而

M(x)={y∈Rn|gi(x)+

〈▽gi(x),y-x〉≤0,i=1,2,…,m},

从而

M(xk)={yk∈Rn|gi(xk)+

〈▽gi(xk),yk-xk〉≤0,i=1,2,…,m}.

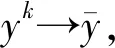
引理 3.3令映射F:Rn→Rn和f:Rn→(-∞,+∞]都是连续的,如果Slater约束规范(13)成立,则映射L在任何有界集上是有界的.

证明假设L在某些有界集C上是无界的,从而存在序列{xk}⊂C,使得‖L(xk)‖→∞.而根据连续函数的有界性,从而F(xk)在C上是有界的.而f也是连续的,从而是有界的;而G-范数是正定的,则根据(18)式知q(xk)→-∞,即q(xk)无下界.

另一方面,对于任意的k,由Slater条件知x0∈M(xk),故有

q(xk)=max{-〈F(xk),y-xk〉+f(xk)-

-〈F(xk),x0-xk〉+f(xk)-f(x0)-

而根据上面{xk}、f(xk)、F(xk)的有界性可知,q(xk)有下界,此时与假设矛盾.故有映射L在任何有界集上是有界的.

定理 3.4(a) 假设F:Rn→Rn是连续映射,f:Rn→(-∞,+∞]是连续映射,以及gi:Rn→R(i=1,2,…,m)是连续可微的,也假设Slater约束规范成立,则由(18)式所定义的函数q在Rn上是连续的.

(b) 假设F:Rn→Rn是连续可微映射,f:Rn→(-∞,+∞]是二阶连续可微映射,以及gi:Rn→R(i=1,2,…,m)是二阶连续可微的,则函数q在任何方向d∈Rn上是方向可微的,以及它的方向导数为

[▽F(x)-▽2f(x)-G](L(x)-x)-

(34)

其中

Λ(x)={λ∈Rm|F(x)+

λi[gi(x)+〈▽gi(x),L(x)-x〉]=0,

λi≥0,i=1,2,…,m}.

(35)

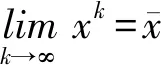
(b) 的证明来自于文献[10]的定理2.

如果要通过优化问题(30)来获得(1)式的解,必须要找到q在S上的全局最优解,因此想要知道在那个条件下(30)式的稳定点是一个全局最优解,那么在接下来的定理中将回答这个问题.在回答这个问题之前,先给出一个引理.

引理 3.6令映射F:Rn→Rn是连续可微函数,f:Rn→(-∞,+∞]是二阶连续可微凸函数,约束函数集gi:Rn→R(i=1,2,…,m)是二阶连续可微的,若d=L(x)=x,那么此时有

q′(x;d)≤-〈d,(▽F(x)-▽2f(x))d〉+

(36)

其中I+={i|gi(x)>0}.

证明由于d=L(x)-x,那么通过二次规划问题(17)的KKT条件,以及找到一个拉格朗日乘子向量λ有

gi(x)+〈▽gi(x),d〉≤0,λi≥0,

(38)

λi[gi(x)+〈▽gi(x),d〉]=0,

i=1,2,…,m.

(39)

通过(34)、(37)和(39)式可以得到

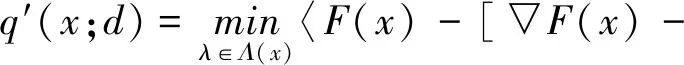
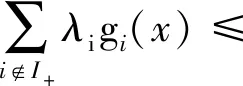
q′(x;d)≤-〈d,(▽F(x)-▽2f(x))d〉+

定理 3.7假设映射F:Rn→Rn连续可微,f:Rn→(-∞,+∞]是二阶连续可微凸函数,且▽F(x)-▽2f(x)是正定的,凸约束函数集gi:Rn→R(i=1,2,…,m)是二阶连续可微的,以及Slater约束规范(12)式成立,如果x∈S对任意的y∈S都有

q′(x;y-x)≥0,

(41)

那么x是一般混合变分不等式MVIP(F,f)的解.

证明假设x∈S满足(41)式，根据Slater条件以及文献[1]中143页的结果可知

M(x)⊂x+cl{α(y-x):y∈S,α>0}, (42)

那么此时根据(41)和(42)式以及q′(x;·)的正齐次性,那么有

q′(x;y-x)≥0, ∀y∈M(x),

(43)

由于当x∈S时满足I+=∅,此时根据引理3.6有

q′(x;L(x)-x)≤-〈L(x)-x,

(▽F(x)-▽2f(x))(L(x)-x)〉,

(44)

而由于L(x)∈M(x),再根据(43)和(44)式得到

〈L(x)-x,(▽F(x)-▽2f(x))(L(x)-x)〉≤0.

而根据题设条件▽F(x)-▽2f(x)是正定的,从而L(x)=x,再根据定理2.4,此时x就是MVIP(F,f)的一个解.