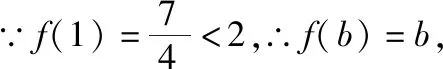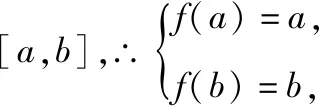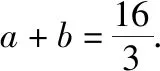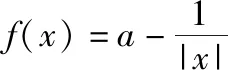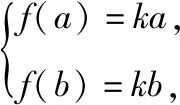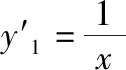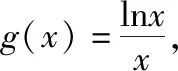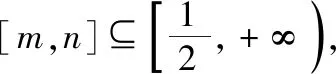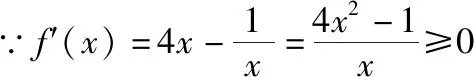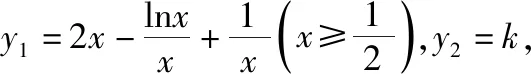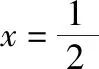常见“保值”问题的求解策略
2019-11-19江苏
江苏
王安寓
(作者单位:江苏省南京市六合区实验高级中学)
在函数的家族中,存在很多天才.这些天才俊杰在数学王国中纵横驰骋呼风唤雨,手段诡秘.有一种对应,将集合A中的元素x保持不变地对应到它自身,我们称其为恒等变换.在恒等变换作用下,函数的定义域与值域相同.神奇的是,不是恒等变换的对应,也能使函数的定义域与值域相同.我们称这类函数为“保值”函数,有的资料也称其为“闭函数”,对应的定义域为“保值”区间.
与“保值”函数有关的题型,主要有三类:①判断一个函数是否是“保值”函数;②求一个函数的“保值区间”;③由函数具有“保值”性求参数范围.而“保值”函数的试题呈现的方式多变,可直接命题,可命制探索性问题或存在性问题等.那么,求解“保值”问题的常用策略有哪些呢?本文作一点探讨,以期抛砖引玉.
策略一、运用常见函数的值域解决“保值”函数
最典型的“保值”函数是一次函数.一次函数的定义域和值域都是(-∞,+∞),根据保值函数的定义可知,一次函数必是保值函数.特别地,一次函数中,y=x恰是恒等变换.除了一次函数外,反比例函数也存在“保值”函数,三角函数也可构造“保值”函数.
【例1】(1)若函数f(x)=(a2-2a-3)x2+(a-3)x+1的定义域和值域都为R,则实数a的取值范围是
( )
A.a=-1或3 B.a=-1
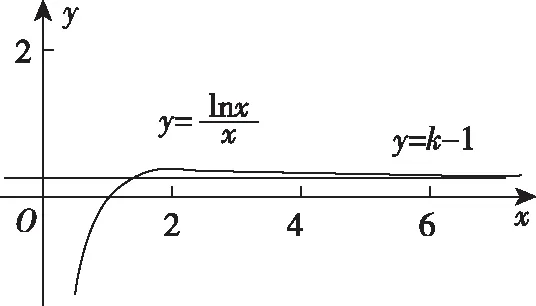
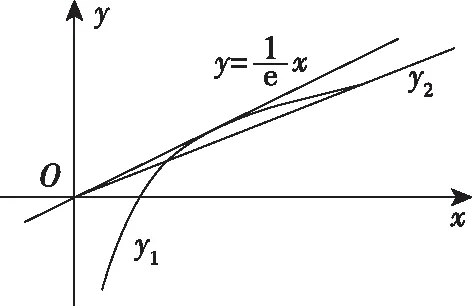
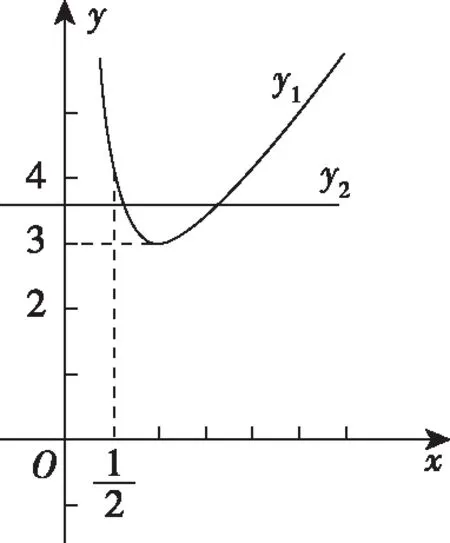
C.a>3或a<-1 D.-1 ②你能根据该题再举出一个含有sinx的“保值”函数吗?你举出的函数为________. 分析:(1)由于函数f(x)的定义域和值域都是R,而f(x)的解析式是最高次方为二次的多项式函数,故f(x)只能是一次函数.由此确定函数的类型进而求解. (2)当x>0时,f(x)>0等价于a2-2a>0,解不等式即可. 解析:(1)若a2-2a-3≠0,则f(x)为二次函数,值域不为R,不合题意; 若a2-2a-3=0,则a=-1或3; 当a=3时,f(x)=1,f(x)的值域为{1},不合题意; 当a=-1时,f(x)=-4x+1,f(x)的值域为R,符合题意. 故选B. (2)依题意得a2-2a>0,解得a<0或a>2.故实数a的取值范围是a<0或a>2. 变式1:若函数f(x)=2x-m是(0,+∞)上的“保值”函数,则实数m的值是________. 答案:m=1. 从数的角度看,若函数f(x)在区间[a,b]上是单调递增函数,且是“保值”函数,则f(a)=a,f(b)=b,即f(x)=x在定义域内有两个不相等的实数根a,b,从而转化为关于x的方程f(x)=x在定义域内有两个不相等的实数根,运用根的分布求解. 从形的角度看,若函数f(x)在区间[a,b]上是单调递增的,且是“保值”函数,由于x∈[a,b]时,f(x)∈[a,b],故f(a)=a,f(b)=b,于是,函数y=f(x)过点(a,a),(b,b),故函数y=f(x)的图象与直线y=x的图象有两个不同的交点.再考虑直线与曲线有两个不同交点的情形,根据相应的几何意义求得参数范围. 1.保值区间,求解方程 对于“保值”函数的“保值”区间,只能通过解方程(组)完成.根据“保值”函数的定义,将“保值”函数转化为方程(组),运用消元法求解.这是最基本的方法. 【例2】已知函数f(x)的定义域为区间A,若f(x)的值域也为A,则称区间A为f(x)的“保值”区间,f(x)是区间A上的“保值”函数. (1)求函数f(x)=x2的形如[n,+∞)(n∈R)的保值区间; (2)设f(x)=x2+m是[a,b]上的“保值”函数,求m的范围及对应y=f(x)的“保值”区间[a,b]. 分析:(1)根据“保值”函数的定义,条件转化为f(x)=x在[n,+∞)上有异根,解方程即可; (2)由“保值”函数的定义,结合函数单调性及最值,转化为方程或方程组求解. 解析:(1)∵x2≥0,且f(x)=x2的值域为[n,+∞),∴n≥0,易知函数f(x)=x2在[n,+∞)上单调递增,∴f(n)=n2=n,解得n=0或n=1,∴函数f(x)=x2的形如[n,+∞)的“保值”区间为[0,+∞)或[1,+∞). (2)易知f(x)=x2+m在(-∞,0]上单调递减,在[0,+∞)上单调递增. ①若a ③当a<0 若f(m)≥f(b),则0 点评:“保值”函数的本质是求函数的最值或值域,而二次函数在区间上的最值问题是学生司空见惯的.当函数在区间上单调递增时,根据函数的单调性,将“保值”函数问题转化为方程的解的问题,可直接解方程或应用根与系数的关系.欲求“保值”区间,必解方程,因此,本题只能运用方程思想(数的角度). 解析:易知f(x)的定义域为R,f(x)为奇函数,且f(x)在R上单调递增.则M=N,得a,b是f(x)=x的两个相异实根.f(x)=x,即x|x|=x,解得x=0或x=±1,注意到a 2.根之分布,参数范围 “保值”函数都是满足一定条件的,而这个“条件”对应的就是参数的范围.已知“保值”求参数,往往转化为根的分布、不等式或两个函数有相异交点问题求解. ( ) 分析:(1)紧抓闭函数定义,转化为方程有解. (2)紧抓闭函数定义,转化为方程有解,进而转化为两个函数有不同交点. 故选D. 点评:先判断函数单调性,再根据函数单调性将闭函数(也是“保值”函数)问题转化为方程有解问题,然后应用根的分布求解,也可直接解出方程,研究方程的根.本题的方法一和方法二的求解过程是从数的角度实施的,方法三是从形的角度求解的. 用形求解,还可以先做适当变形,再画图求解(方法二和方法三). 对比三种方法,方法二最直观,既便于观察又避开了切线的难点.方法三平移抛物线,不如平移直线,相对来说不便于操作. 当然,本题还可仿照例3(1)的前两种方法从数的角度求解. ( ) A.[-1,0] B.[1,+∞) 解析:易知函数f(x)是[1,+∞)上的增函数. 故选D. 3.韦达定理,函数最值 “保值”函数问题转化为方程的解,可利用韦达定理,将目标转化为关于参数的函数最值问题求解. 分析:先判断函数单调性,再转化为方程有不等实根,应用韦达定理,构造关于t的函数求解. 点评:将“保值”函数转化为方程有异根后,巧用韦达定理将目标转化为关于t的函数,通过配方求得目标的最大值.本题的求解过程充分体现了转化与化归思想、函数与方程思想.本题容易遗漏求参数范围——新函数的定义域. a+b=4+4m∈(4,6]. 从形的角度看,若函数f(x)在区间[a,b]上单调递减,且是“保值”函数,由于x∈[a,b]时,f(x)∈[a,b],故f(a)=b,f(b)=a,于是,函数y=f(x)过点(a,b),(b,a),故函数y=f(x)的图象与直线y=-x+a+b有两个不同的交点.再考查直线与曲线有两个不同交点的情形,根据相应的几何意义求得参数范围. 分析:由函数的单调性,将值域转化为方程组,研究方程组有不同实数解即可. 若函数f(x)既有增区间又有减区间,又是“保值”函数,则分类讨论,在各单调区间内研究函数值域,各个击破.在增区间内,用策略二;在减区间内,用策略三;在既有增区间又有减区间的区间内,先确定一个最值,再讨论第二个最值. 1.分类讨论,各击“保值” “保值”函数本质是求函数y=f(x)在定义域为[a,b]时的值域.当函数单调性不止一种时,就要分类讨论,各个击破. 分析:二次函数f(x)既有单调递增区间,又有单调递减区间,由f(x)的定义域[a,b]求函数f(x)的值域,就要分类讨论. 故答案为5. 解析:显然m,n同号. 综上,实数a的取值范围为a=0或a>2. 2.联袂导数,共谋“保值” 当“保值”函数的形式复杂,不易判断函数单调性时,可借助导数研究函数的单调性. 【例7】若函数g(x)=x-ln(x+m)的“保值”区间是[2,+∞),求实数m的取值范围. 分析:考虑两个方面:①函数g(x)在[2,+∞)上有意义;②如何求函数g(x)的值域. 解析:由x+m>0得x>-m,因为g(x)的“保值”区间是[2,+∞),所以2+m>0,即m>-2. 当2≤1-m,即-2 当2>1-m,即m>-1时,函数g(x)在[2,+∞)上单调递增,故g(x)min=g(2)=2,即2-ln(2+m)=2,解得m=-1,与m>-1矛盾,舍去. 综上,m=-1. 点评:对于复杂函数的单调性,常用导数作为手段来研究. 变式7:已知函数f(x)=x3+ax+b的图象关于原点对称,且与x轴相切. (1)求实数a,b的值; (2)是否存在实数m,n,使得g(x)=3-|f(x)|在区间[m,n]上的值域仍为[m,n]?若存在,求出m,n的值;若不存在,请说明理由. 解析:(1)a=b=0,过程略;(2)易知g(x)=3-|x3|在(-∞,0]上单调递增,在[0,+∞)上单调递减. 当n>m≥0时,g(x)=3-x3在[m,n]上单调递减,则g(m)=3-m3=n,g(n)=3-n3=m,两式相减得n3-m3=n-m,n2+mn+m2=1,0 当m<0 综上,不存在满足题意的m,n. 通过例2-例7的求解,我们得到解决“保值”函数问题的步骤:先研究函数的单调性,再根据函数的单调性情况实施转化.若能判断“保值”函数是增函数,则运用策略二;若能判断“保值”函数是减函数,则运用策略三;若“保值”函数既有增区间又有减区间,则运用策略四. 求解“k倍”函数、“镜像”函数、“调和”函数、“平方”函数等函数问题的方法与求解“保值”函数问题的方法基本相同,仍可从数(方程或方程组)的角度和从形(转化为根的分布或两个函数的交点)的角度两个角度入手转化求解. 【例8】对于函数y=f(x),若存在区间[a,b],当x∈[a,b]时,f(x)的值域为[ka,kb](k>0),则称y=f(x),x∈[a,b]为“k倍”函数.若f(x)=lnx+x是“k倍”函数,则实数k的取值范围是________. 分析:由函数的单调性破解“k倍”函数的本质,转化为方程有解. 方法二:仿方法一得lnx+x=kx有两个相异正根,即lnx=(k-1)x有两个相异正根. 设函数y1=lnx,y2=(k-1)x,则转化为y1与y2的图象有两个相异的交点.y2是过原点的直线. 通过例8的求解,我们得到解决类“保值”函数问题的方法同于“保值”函数问题.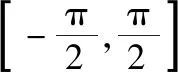
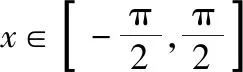
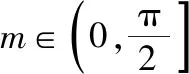
策略二、单调递增“保值”函数,转化为方程有异根
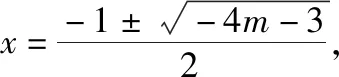
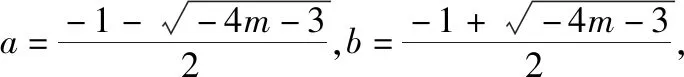
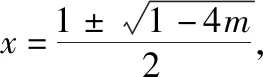
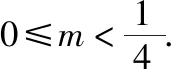
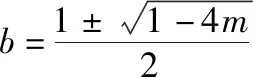
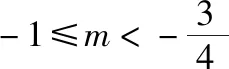
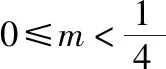
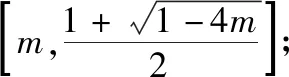
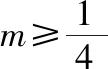
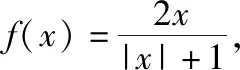
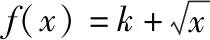
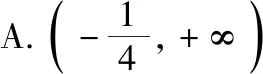
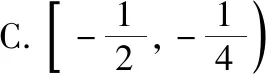
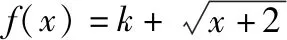
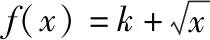
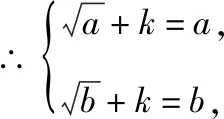
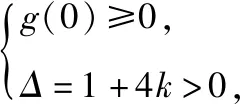
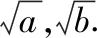
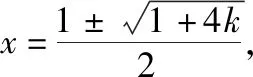
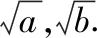
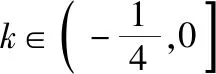
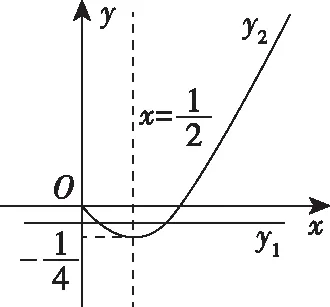
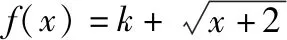
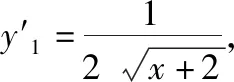
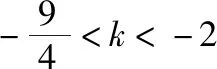
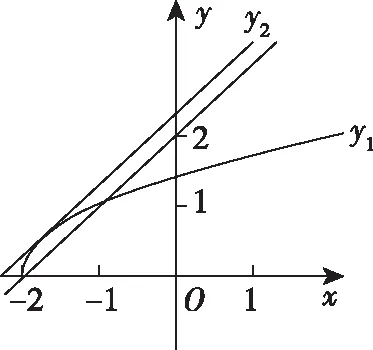
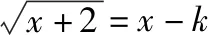
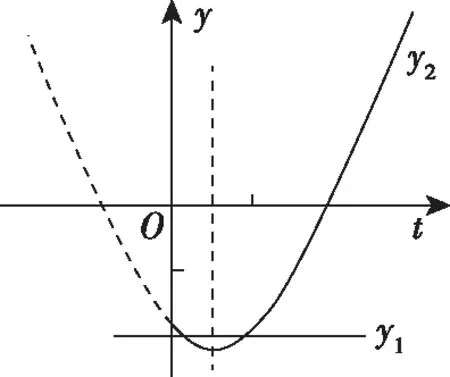
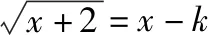
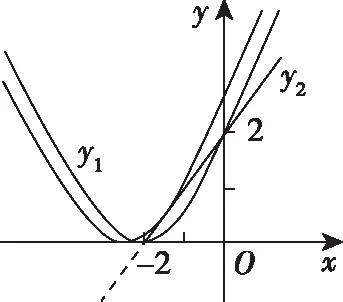
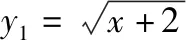
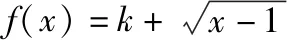
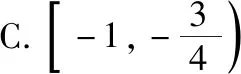
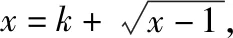
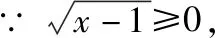
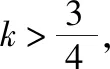
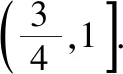
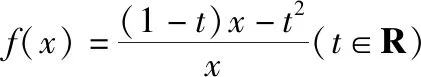
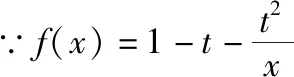
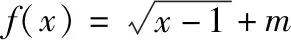
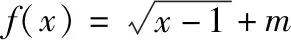
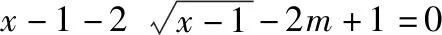
策略三、单调递减“保值”函数,转化为方程组有两解
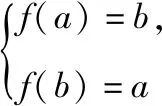
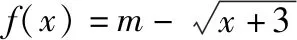
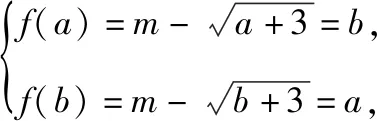
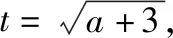
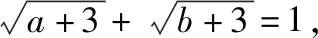
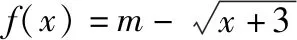
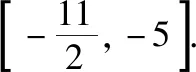
策略四、不单调“保值”函数,分类讨论各个击破