追本溯源,发现本质
——对教材中椭圆一个定值问题的深度探究与微拓展
2019-11-19广东
广东
潘巧玲
(作者单位:广东省东莞市麻涌中学)
在强调高考改革的今天,越来越多的高考试题呈现出回归教材的趋势,出题人通过改编、创新等手段赋予高考典型试题新的生命,这是高考命题的一种新走向.下面是笔者对教材中椭圆一个定值问题的深度探究,并对试题进行变式与微拓展,以引起各位同行重视.
一、探究背景
高考命题呈现出回归教材的趋势,回归教材的目的就是要寻“源”.教材是很好的母题库,每年高考试题中出现不少让学生感到陌生的题目,实际上大多数高考题都是由教材例题或习题改编而来的,恰当的变式与微拓展可以帮助学生架起一座知识与知识之间的桥梁,让学生在已知水平和未知水平之间自然过渡,但“万变不离其宗”,因此教师要引领学生在解决问题后,进一步挖掘其中的教学价值.深度探究也是让学生建立充足的知识储备的过程,在解题时就能得心应手.下面是教材中椭圆的一个定值问题.
题目1(人教A版选修4-4第15页习题1.3第6题)已知椭圆的中心为O,长轴、短轴的长分别为2a,2b(a>b>0),A,B分别为椭圆上的两点,且OA⊥OB.
(2)求△AOB面积的最大值和最小值.
分析:在圆锥曲线中定点定值问题是高考数学解析几何类试题考查的热点问题,其中定值问题一般选择坐标法和参数法解题,利用圆锥曲线的性质找等量关系.
二、探究过程
1.解法探究
试题解答:第(1)问,
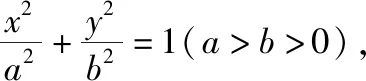
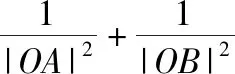
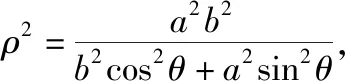
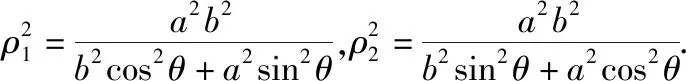

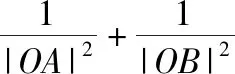
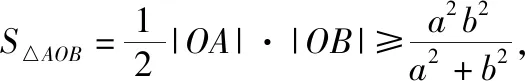
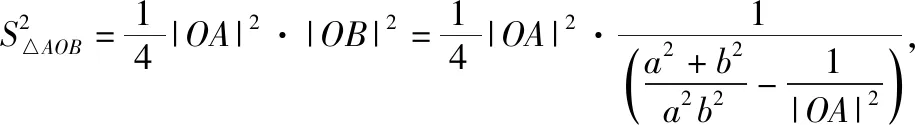
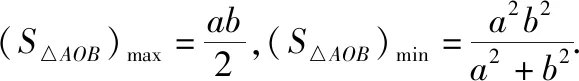
2.试题呈现
教材中的这个习题,不禁让笔者想起了高三二轮复习中的一个模拟试题.
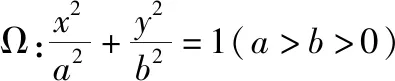
(1)求椭圆Ω的标准方程;
(2)设直线l′交椭圆Ω于C,D两点,且OC⊥OD,求证:O到直线l′的距离为定值.
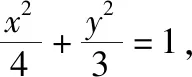
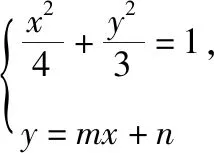
当直线l′的斜率不存在时,设直线l′的方程为x=x0.
3.双曲线中定值问题的探究
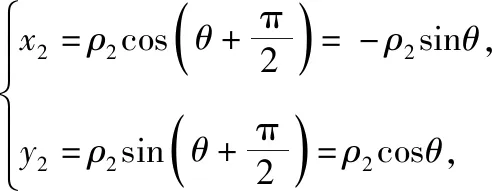
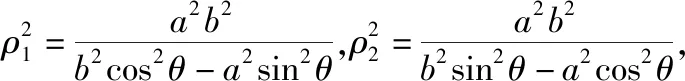
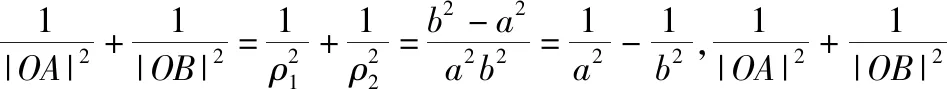
椭圆和双曲线在解析几何中处于重要的地位,有很多类似的性质,两者之间密切联系,规律和谐,辩证统一.如果我们用类比的方法去学习这两部分的知识,可起到事半功倍的效果.有了以上两个题目做基础,我们发现椭圆中有的结论,双曲线中也会有类似的结论.
4.椭圆、双曲线中定值的类比
通过以上的证明,笔者发现题目1,题目2所出现的定值不是偶然,而是它们本身蕴含的规律,于是有了以下结论:
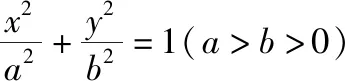

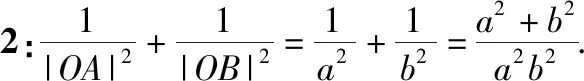
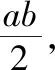
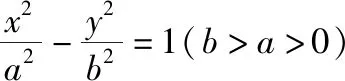
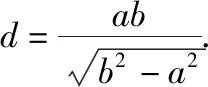
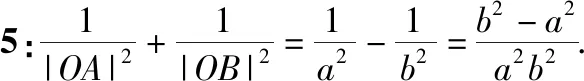
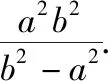
从椭圆到双曲线的类比,将直观想象、逻辑推理和数学运算等数学核心素养融为一体,能有效地培养学生的逻辑思维能力、合情推理和探究能力.当然类比的结论不一定完全相同,也不一定适用,是否正确需要逻辑证明验证.
三、试题变式与微拓展
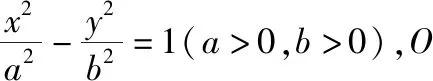
(1)求双曲线的方程;
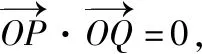
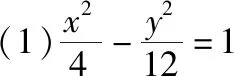
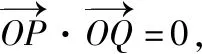
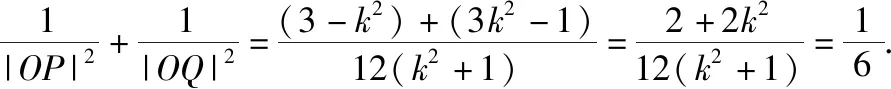
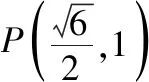
(1)求椭圆C的方程;
(2)斜率为定值k的直线l与椭圆C交于A、B两点,且满足|OA|2+|OB|2的值为常数(其中O为坐标原点).
(ⅰ)求k的值以及这个常数;
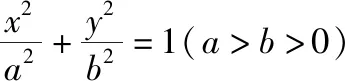
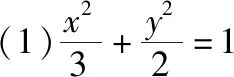
(2)(ⅰ)设直线l的方程为y=kx+b,设A(x1,y1),B(x2,y2),
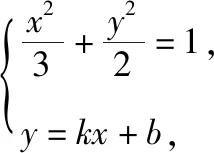
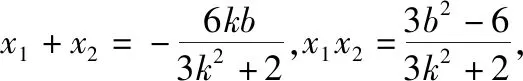
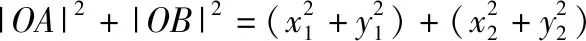
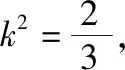
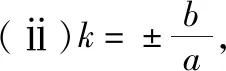
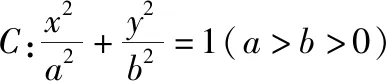
(1)求椭圆C的方程;
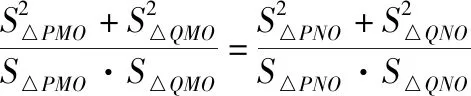
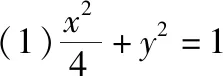
(2)证明:由题意可知直线l的斜率存在,且不为0.设直线l的方程为y=kx+b(b≠0),点P,Q的坐标设为P(x1,y1),Q(x2,y2),令x=0可得y=b,即|NO|=|b|,
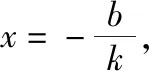
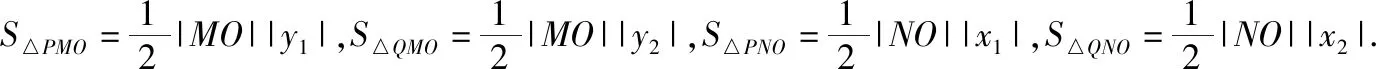
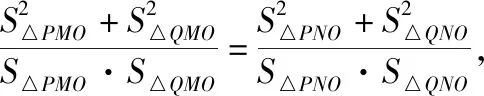
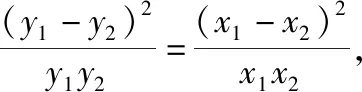
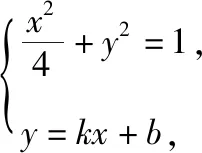
Δ=64k2b2-4(1+4k2)×4(b2-1)>0,即1+4k2-b2>0.
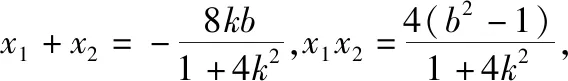
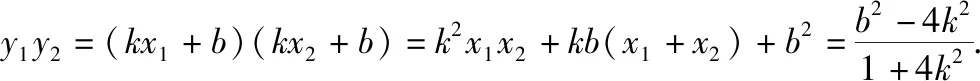
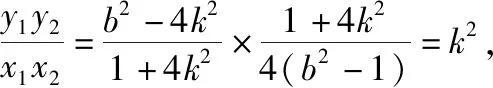
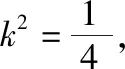
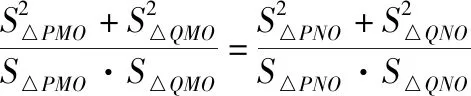
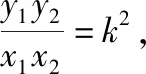
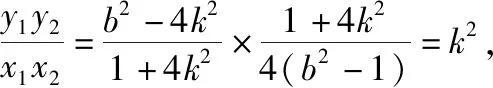
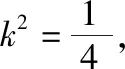
如果教师在课堂上仅处理椭圆与双曲线的定值问题就结束了,那么这道教材例题的价值就没有被充分挖掘出来.通过以上四个变式探究与微拓展,激发了学生探究数学的兴趣和热情,同时在探究的过程中,教会学生学会学习,学会发现问题并解决问题.通过变式教学,在探究问题和解决问题的过程中,调动学生的积极性,培养学生的逻辑思维,加深同学们对知识的理解程度,进一步把握知识的本质与联系.
四、教学反思
1.激活教材,融会贯通
通过对教材中椭圆一个定值问题的深度探究,引出了多个变式拓展,通过变式再反思,又得到了很多结论.因此,笔者的感触是,教材习题是值得挖掘的,而且是大有挖掘的价值,不要轻易放过教材中的任何一道题目,唯有以教材为本源,深度挖掘教材,灵活利用教材,才能让高三复习真正“回归教材”,才能温故知新.教材的每道例题、习题都有它存在的价值,它们是专家经验的积累,智慧的结晶,所以教师要学会引领学生做深度研究,教材永远是命题的本源,教会学生利用好教材,善于积累.总之,课堂教学要遵循以教材为主的原则,既没有过时,更不能停留在口号上,如果教学中对例题的讲解仅仅是照本宣科,忽视例题的典型示范作用,那么就不能让学生体会到例题中蕴含的解题思想和方法,因此教师可以通过改编教材习题中的某些条件或结论,得到解决一类问题的方法,从而充分发挥它们的教学功能.
2.重视探究,触类旁通

