“经典”高考试题对教学的启示
——2013年陕西卷理科第20题对解析几何教学的启示
2019-11-19福建
福建
陈玉兰 吴志鹏
(作者单位:福建省德化第一中学)
“经典”的试题之所以能成为后续教与学的示范,主要是试题的命制为教学提供了可模拟、可变式、可拓展和可借鉴的典范,具有很强的操作性和参考价值,很多高考试题都具备这种功能,能启迪教师的教学.下面以2013年陕西卷理科第20题为例进行说明.
一、“经典”试题
1.(2013·陕西卷理·20)已知动圆过定点A(4,0),且在y轴上截得弦MN的长为8.
(Ⅰ)求动圆圆心的轨迹C的方程;
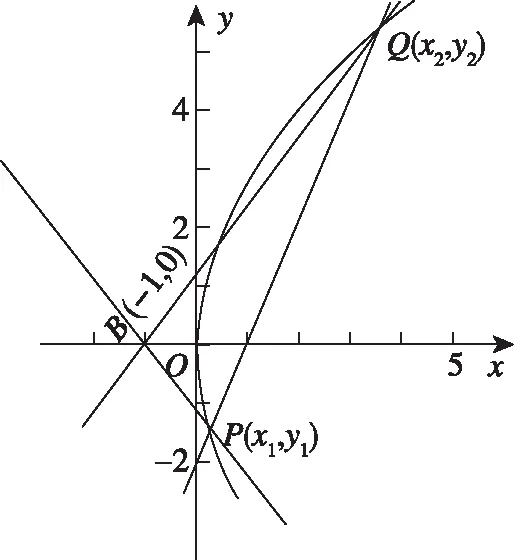
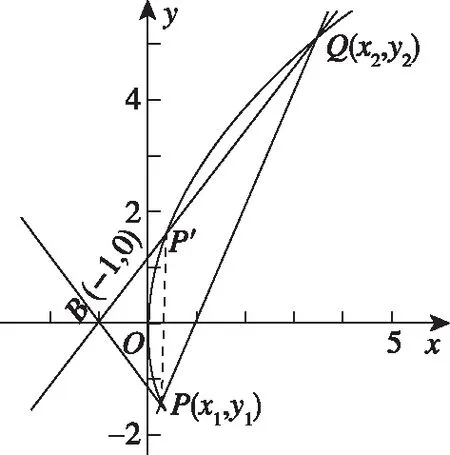
(Ⅱ)已知点B(-1,0),设不垂直于x轴的直线l与轨迹C交于不同的两点P,Q,若x轴是∠PBQ的角平分线,证明直线l过定点.
二、又现新题
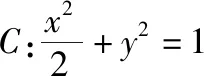
(Ⅰ)当l与x轴垂直时,求直线AM的方程;
(Ⅱ)设O为坐标原点,证明:∠OMA=∠OMB.
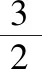
(Ⅰ)若|AF|+|BF|=4,求l的方程;
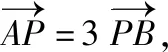
三、试题对比
1.总体印象
2013年高考数学陕西卷理科第20题与2018年全国卷Ⅰ理科第19题、2019年全国卷Ⅰ理科第19题在整体上很相似,虽然我们并不知道命题专家是否以这道高考题为“原型”或参考这道高考题进行2018年和2019年这两道解析几何试题的命制,但2018年和2019年的这两道解析几何问题的设置确实与之有着“异曲同工”之妙:2018年全国卷Ⅰ理科第19题适当变换了2013年陕西卷理科第20题的条件,将抛物线变换成了椭圆,而第二小题都是以角平分线为载体进行问题的设计,相似度很高;2019年全国卷Ⅰ理科第19题只是适当变换了2013年陕西卷理科第20题的结论,将角平分线的问题改成了以向量为载体求弦长的问题,同样也是“一脉相承”.
2.共同特征
它们考查的都是圆锥曲线的定义及其相关的几何问题等核心知识,题目均能很好地贯彻、落实新课程标准,即了解圆锥曲线的实际背景,感受圆锥曲线在刻画现实世界和解决实际问题中的作用;能用坐标法解决一些与圆锥曲线有关的简单几何问题(直线与圆锥曲线的位置关系)和实际问题.题目设置具有条件简洁、文字符号少、立意鲜明和结构精巧等共同特征,考查的内容为“角平分线”“向量相等”和“直线与圆锥曲线的位置关系”,对每个考生来说,都很熟悉,题目的入口宽,解题思路多样;试题的第二问,从知识角度看,能够考查学生对直线的方程、弦长的计算、角平分线的性质、圆锥曲线的几何性质及直线与圆锥曲线的位置关系的理解程度;从数学思想方法看,考查了数形结合思想、函数与方程思想和化归与转化思想等数学思想方法;从能力角度看,考查了推理论证能力和运算求解能力,本题仍是解析几何解答题的典型题,第二问不外乎用“三步曲”:第一步联立直线的方程与圆锥曲线的方程,寻求坐标之间的关系;第二步利用几何条件转化为用坐标表示,或是利用向量相等进行坐标转化;第三步,将第二步的结果代入第一步的表达式中得到结果——这几乎是解析几何问题的最终归宿,试题虽然常规,但却能有效地考查学生的层次性和差异性,主要表现在通过对所提供的条件以及对有关概念的准确理解,通过运算和推理获得证明;通过图形抓住问题的本质,得到不同的解题思路,这样既考查学生抓住数学问题本质的灵敏度,又能考查学生思维的创造性.
3.兼具特色
2013年陕西卷理科第20题把学生熟悉的“角平分线”与x轴巧妙结合,从而凸显试题图形的对称性,又使得试题的难度值下降,2018年全国卷Ⅰ理科第19题也正是如此;2019年全国卷Ⅰ理科第19题则是考查学生利用向量的“工具”即“坐标法”进行解题的能力,同样使试题的计算量减少了很多,难度也有很大的下降,更符合新课标让学生“多思少算”的思路.试题中图形的巧妙结合,给考生创设了更多成功的机会,这样的高考题自然成为高考复习训练中教师优先选择的典型题目.题目设计的“巧”与“活”为相似的三道高考试题注入了“灵性”,其所蕴含的思想方法凸显在文字、符号和图形中,这样的题目无疑是高考题中的经典,也是今后教学中值得关注和研究的问题.
四、利用对2013年陕西卷理科第20题的解法探究,实现学生思维的多向发展
对于第一问,容易求得C的轨迹方程为y2=8x,下面仅对第二问进行解法探究.
思路1:利用点斜式设出直线l的方程为y=kx+b,与抛物线C联立,得到一个一元二次方程,由根与系数的关系得到两根的和与积,并利用x轴是∠PBQ的角平分线的性质(kQB+kPB=0)得到P,Q两点的坐标关系式,进而化简直线的方程,通过方程求得直线所过的定点.
解法1:证明:设直线l的方程为y=kx+b(k≠0),
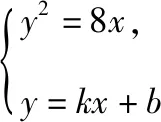
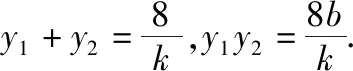
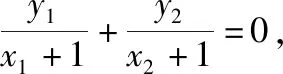
y1(x2+1)+y2(x1+1)
=y1x2+y2x1+(y1+y2)
由已知得y1+y2≠0,所以y1·y2=-8,即k=-b,此时Δ>0.
故直线l的方程为y=k(x-1),过定点(1,0).
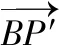
解法2:证明:设直线l的方程为y=kx+b(k≠0),
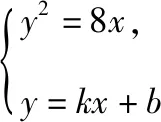
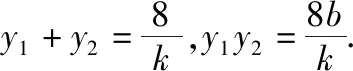
若x轴是∠PBQ的角平分线,则点P关于x轴的对称点为P′,
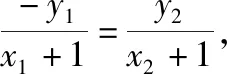
y1(x2+1)+y2(x1+1)
=y1x2+y2x1+(y1+y2)
由已知得y1+y2≠0,所以y1·y2=-8,即k=-b,此时Δ>0.
故直线l的方程为y=k(x-1),过定点(1,0).
解法3:证明:设直线l的方程为y=kx+b(k≠0),
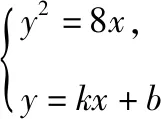

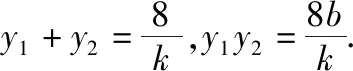
若x轴是∠PBQ的角平分线,点P关于x轴的对称点为P′,
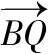
则y1(x2+1)+y2(x1+1)=y1x2+y2x1+(y1+y2)
由已知得y1+y2≠0,所以y1·y2=-8,即k=-b,此时Δ>0.
故直线l的方程为y=k(x-1),过定点(1,0).
思路2:由于∠PBQ被平分的两个角和抛物线都关于x轴对称,即点P关于x轴的对称点P′在直线BQ与抛物线的交点上,即B,P′,Q三点共线,所以我们可以从直线BQ方程与抛物线C联立的思想寻找条件,从而获得解法4.
解法4:证明:设直线l的方程为y=kx+b(k≠0),
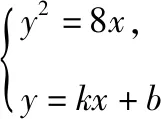

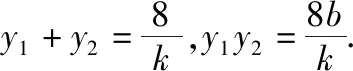
若x轴是∠PBQ的角平分线,则点P关于x轴的对称点P′在直线BQ上.
令直线lBQ的方程为x=my-1,
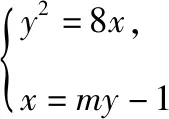
其中Δ>0,
则(-y1)·y2=8,即y1y2=-8,
即k=-b,此时Δ>0.
故直线l的方程为y=k(x-1),过定点(1,0).
思路3:利用两点式设出直线lPQ的方程,即直线lPQ的方程为8x-(y1+y2)y+y1y2=0,同理我们可以假设直线lP′Q(点P(x1,y1)关于x轴的对称点P′(x1,-y1))的方程为8x-(y2-y1)y-y1y2=0,直线lP′Q过点B(-1,0),所以y1·y2=-8,此种方法大大减少了计算量,从而得到解法5.
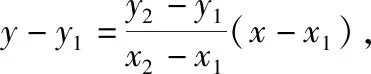

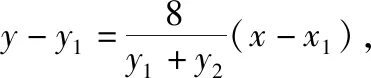
因为x轴是∠PBQ的角平分线,则点P(x1,y1)关于x轴的对称点P′(x1,-y1)也在抛物线上,所以直线lP′Q的方程为8x-(y2-y1)y-y1y2=0,
因为直线lP′Q过点B(-1,0),所以有y1·y2=-8,
直线lPQ的方程可化为-(y1+y2)y+8(x-1)=0,
故直线过定点(1,0).
解法6:猜想直线lPQ过定点M(1,0),证明如下:
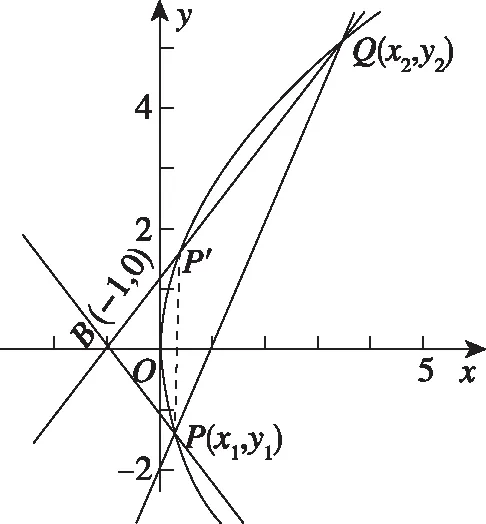
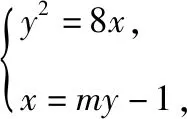
其中Δ>0,
令P(x1,y1),Q(x2,y2),
则(-y1)·y2=8,即y1y2=-8,
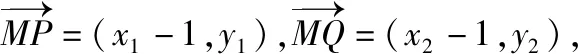
因为(x1-1)y2-(x2-1)y1
=x1y2-y2-x2y1+y1
2018年全国卷Ⅰ第19题与2019年全国卷Ⅰ第19题,也存在多样的探究思路,具有很强的广阔性,也能够迁移以上方法进行求解,有兴趣的读者可自行整理.
五、利用对2013年陕西卷理科第20题的变式与拓展实现高效率的教与学
方案1:适当改变条件,而不改变结论
变式1:已知抛物线C:y2=2px(p>0)和点B(-m,0)(m≠0),设不垂直于x轴的直线l与C交于不同的两点P,Q,若x轴是∠PBQ的角平分线,证明直线l过定点M(m,0).
变式2:将条件中的抛物线改成椭圆可得2018年全国卷Ⅰ理科第19题.
方案2:适当改变结论,而不改变条件
变式3:将结论中角平分线的条件变换成向量相等可得2019年全国卷Ⅰ理科第19题.
方案3:将条件和结论进行适当变换后重新组合
变式4:已知抛物线C:y2=2px(p>0)和点B(-m,0)(m≠0),过点M(m,0)且不垂直于x轴的直线l与C交于不同的两点P,Q,证明:∠PBO=∠QBO.
变式5:已知抛物线C:y2=2px(p>0)和点B(-m,0)(m≠0),过点M(m,0)且不垂直于x轴的直线l与C交于不同的两点P,Q,若点P关于x轴的对称点为P′.证明:P′,M,Q三点共线.
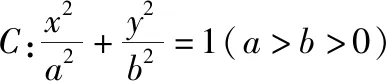
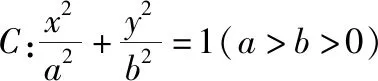
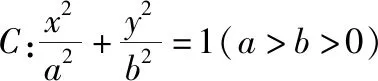
变式方案有很多,进行变式研究与结论拓展是高效教学的一个重要方法,从2013年陕西卷理科第20题的变式与拓展中,我们能够很好地感受其对学生数学素养形成的良好作用以及对教学的启迪与示范.
六、反思与感悟

