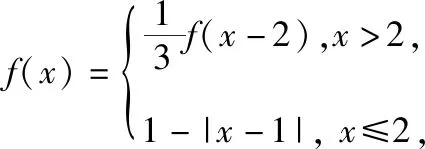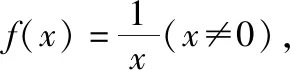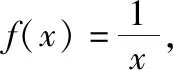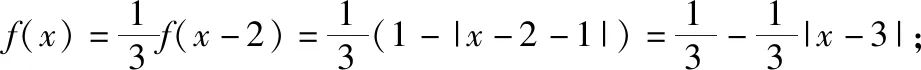方程实根问题类析
2019-11-19江西
江西
孙春生
(作者单位:江西省吉水中学)
方程实根问题涉及方程实根(函数零点)的个数、各实根之和以及参数的取值范围等,常要依据函数的单调性、周期性及函数图象的对称性等性质,利用函数零点存在性定理,结合数形结合、分类与整合、函数与方程和化归与转化等数学思想来解决.此类题型经常出现在试卷客观题的最后一道题中,有一定的难度,能综合考查学生的抽象概括能力与直观想象核心素养,受到各类考试命题人的青睐.
一、形如f(x)=m的方程实根问题
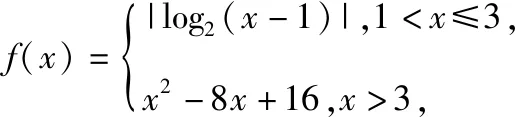
( )
A.6 B.7
C.8 D.9
【思路分析】本题要先画出f(x)的图象,利用函数图象的对称性得出x3+x4的值,再利用对数的运算性质得x1x2=x1+x2,代入要求的式子,即可解决问题.
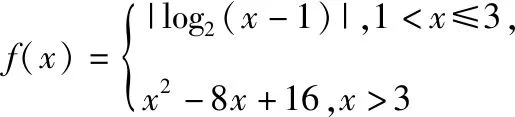
即有(x1-1)(x2-1)=1,则x1x2=x1+x2,
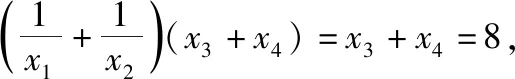

【评析】解决此类分段函数的零点问题,需要画出相应分段函数的图象,并通过图象的对称性和函数的性质来解决问题.本题对基本初等函数的图象的画法要求比较高.
二、形如f(x)=g(x)的方程实根问题

【思路分析】本题将函数周期性和奇偶性等性质融为一体,需要利用相关性质画出函数的图象,通过数形结合来解决问题.
解:如图,作出函数f(x)与g(x)的图象,
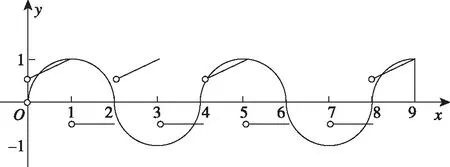

要使关于x的方程f(x)=g(x)有8个不同的实数根,


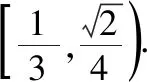
【评注】本题考查分段函数的应用,函数的奇偶性与周期性,要求在作图时关注性质及区间的端点值,注意直线与曲线的交点与切点,正确画出函数图象,利用数形结合思想来解决问题.
三、形如f(f(x))=a的方程实根问题
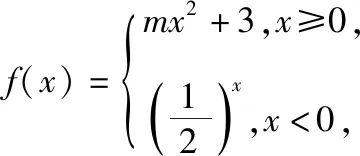
( )
A.(1,3] B.[1,3]






(3)当m<0时,作出f(x)的函数图象,如图所示:


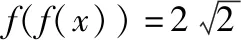
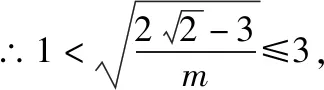
【评注】对于y=f(f(x))-a的零点问题,一般要先设内函数f(x)=t,解出相应的t的值,然后再利用函数y=f(x)与y=t的图象交点来解决问题.
四、形如f(g(x))=a的方程实根问题

【思路分析】本题要设内函数x2-x=t,作出函数y=f(t)的图象,通过中间变量t的转换,利用函数图象的交点来解决.
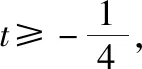

【评注】此类题常用换元法设内函数,通过中间变量(既是内函数的函数值,又是y=f(t)的自变量)来解决问题.在解题过程中,要注意将方程实根转化为两个函数图象的交点问题.
五、形如f2(x)+af(x)+b=0的方程实根问题
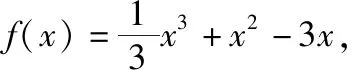
【思路分析】引入中间变量m=|f(x)|,画出函数y=|f(x)|的大致图象,通过观察,要得到12个不同的实根,可得m的范围及m的个数,再通过m2+tm+1=0在指定范围内实根个数求出参数t的范围.
解:由函数的解析式可知f′(x)=x2+2x-3=0,解得x1=-3,x2=1,
由f′(x)>0得x>1或x<-3,即函数在(-∞,-3),(1,+∞)单调递增,
由f′(x)<0得-3 【评注】此类问题往往根据条件限制,先由m=|f(x)|得出中间变量m的范围,再转化为二次方程f2(x)+af(x)+b=0的根的分布问题. ( ) A.2 B.3 C.4 D.5 解:由xf(x)-1=0得xf(x)=1, 当x=0时,方程xf(x)=1不成立; 当4 作出h(x)的图象,由图象知两个函数图象有3个交点,即方程实根的个数为3,故选B. 【评注】本题主要考查函数与方程的应用,利用条件转化为两个函数图象的交点个数问题,利用数形结合是解决本题的关键,难点是利用函数递推性质求不同区间的函数表达式.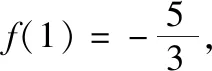
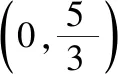
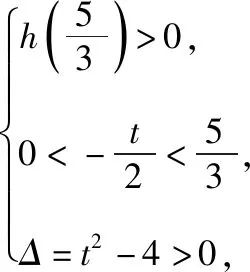
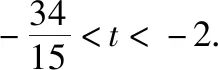
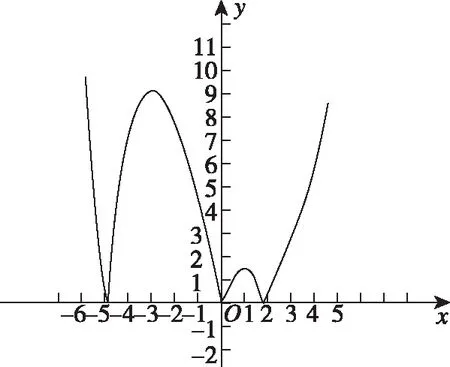
六、形如的方程实根问题