从数学概念教学到数学模式的形成
——谈《函数奇偶性》的教学
2019-11-19江苏
江苏
郑宝生 潘 鑫
(作者单位:江苏省无锡市立人高级中学)
李邦河院士曾经说过,数学根本上是玩概念的.因为数学概念是具有共性特征事物的抽象,也是对所研究对象的一种分类,它是人类理性思维的成果,也是人类智慧的结晶.让学生理解和掌握数学概念,就要让学生了解数学概念的起源、形成和发展,在这个过程中寻找方法,在方法中提炼模式.正如张景中院士在谈到数学教育时提出了三条原理:“在学生头脑里找概念,从概念里产生方法,方法要形成模式.”这三条原理在我们的数学课堂教学中也同样适用,它所反映的是概念要直观、亲切,方法要迅速、简明,模式要通用、有力.
一、在学生头脑中找概念
函数是高中数学中最重要的内容之一,而函数的奇偶性也是函数的一个重要性质,对于函数奇偶性的教学设计也经常见诸各种文章之中,怎样的教学设计才能凸显概念中的“任意性”,让学生更好地体悟和理解“任意”的内涵?笔者进行了如下尝试.
问题1:对称是我们生活中最常见的现象,请说出一个轴对称图形和一个中心对称图形;我们学过的函数图象中哪些图象是轴对称图形,哪些图象是中心对称图形?
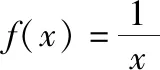
问题2:从图象上看函数f(x)=x2的图象关于y轴对称,仅靠观察是不可靠的,你能举例说明吗?
【意图】让学生自己去发现对称点的函数值相等,如f(0)=f(0),f(-1)=f(1),f(-2)=f(2)等.
问题3:你能写出上述所有等量关系吗?
【意图】举几个例子学生可能会感到轻松,但是若要举出所有的例子学生会感到很惊愕!生命有限,例子无限,从而产生认知冲突,激发学生去思考,找到解决问题的办法.用字母替代数字,对任意的x,都有f(-x)=f(x),学生从中体会到x的“任意性”,在悄无声息中进行了一次数学抽象,它所反映的是从量变到质变的一个哲学思考.
形成结论:函数y=f(x)的图象关于y轴对称,满足的关系式为定义域内任意的x都有f(-x)=f(x).此时学生对于“任意”的理解仅浮于表面,认为“任意”的存在不是必要的,所以教师还需要强化“任意”在定义中不可或缺的地位.
问题4:反之,对于函数y=f(x),定义域内若存在x=1,且满足f(-1)=f(1),能否说明函数y=f(x)的图象关于y轴对称?
【意图】学生可以举例进行反驳,让学生从反面理解偶函数中“任意性”不可或缺的地位.
问题5:定义域内存在x=m,满足f(-m)=f(m),能否说明函数y=f(x)的图象关于y轴对称?存在x=n,满足f(-n)=f(n),能否说明函数y=f(x)的图象关于y轴对称?依此类推,一直这样下去,怎样才能保证函数y=f(x)的图象关于y轴对称?
【意图】从函数定义域内存在x一直延伸到无数个x,最后达到定义域内任意的一个x都满足f(-x)=f(x),缺少定义域内任意的一个x,就不能保证函数y=f(x)的图象关于y轴对称.
形成结论:若定义域内任意的x都满足f(-x)=f(x),则函数y=f(x)的图象关于y轴对称.此时“任意性”不再是多余词汇,而是一个保证定义域内所有的x一个都不能少的关键性词语,然后形成偶函数定义,并深切地体悟到“任意”的分量.只有从学生头脑中构建出来的概念,学生才能更好地理解概念,准确地运用概念.
二、在概念里找方法
问题是数学的心脏,数学概念的学习也是为了更好地解决问题,正如波利亚所告诫我们的,“回到定义中去”.定义中体现的是数学的本质,包含着解决问题的方式方法,这样的方式方法最简单、最有效.
1.证明函数的奇偶性,经历概念的模仿过程
证明函数的奇偶性,让学生运用定义解决问题,归纳操作流程,在回顾反思的过程中,促使学生理解定义的内涵,把握定义的外延.
例1.判断下列函数的奇偶性
(1)f(x)=2x;(2)f(x)=x2-1;(3)f(x)=x3+5x;(4)f(x)=x4+2x2.
思考:(1)证明函数奇偶性的操作步骤是什么?
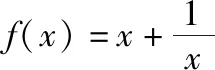
【意图】通过证明函数的奇偶性让学生归纳和概括操作步骤:①定义域;②任意性;③比较f(-x)与f(x).其次通过学生的举例,一方面可以反馈学生对奇、偶函数的认知;另一方面也是为了提炼更一般的方法:对于定义域为R的多项式函数,都是奇次项的是奇函数,都是偶次项或常数项的是偶函数.
对于高一的新生来说,这样的代数证明还是有点难度.他们容易忽略函数的定义域,特别是定义域内x的“任意性”,即使学生求出f(-x)=f(x)或f(-x)=-f(x)也仅仅是停留在符号层面,不理解其中的含义.其主要原因是大部分学生都处于模仿状态,他们还感受不到定义域和任意性是不可缺少的条件,他们的书写也仅仅是照搬而已.所以需要强化定义域和任意性的教学,特别是对于奇、偶函数的符号表达,需要学生能用自己的语言叙述,如-x的函数值与x的函数值相等或互为相反数,使符号含有学生熟悉的具体内容,便于理解和掌握.
2.证明函数不具有奇偶性,经历概念的感悟过程
要理解一个事物,需要从不同角度观察思考,这样才能更好地触及事物的全貌,体会到事物的本质.从反面理解函数奇偶性的定义,能更好地理解定义域和x的任意性.
例2.判断下列函数的奇偶性
思考:(1)你能从中发现奇偶函数有怎样的特点?给出解释.
(2)怎样才能证明一个函数不具有奇偶性,为什么?
【意图】前面两个函数给出了定义域,后面两个函数要求学生先求出定义域,再判断奇偶性.让学生通过对比发现,奇、偶函数的定义域关于原点对称,理由是定义域内的任意x都有f(-x)=f(x)或f(-x)=-f(x),只要在定义域内找到一个x不符合要求,就不具有奇偶性.同样要证明一个函数不具有奇偶性,只要在定义域内举一个反例即可,再结合图象给出具体而形象的解释.
上述的两个问题,一个是正面说明,另一个是反面揭示,体现一个本质:对于定义域内任意的x值或对应的函数值,只要有一个x值不满足函数的奇偶性定义,则这个函数就不具有奇偶性.一方面可以让学生准确地掌握函数奇偶性的定义,发现奇、偶函数的定义域关于原点对称;另一方面让学生体会到“定义域内任意的x”在函数奇偶性定义中不可缺少的作用,并提供证明函数不具有奇偶性的一种方法.
3.已知函数的奇偶性求字母系数,经历方法的辨析过程
已知函数的奇偶性,回到定义中去,就是定义域内任意的x都有f(-x)=f(x)或f(-x)=-f(x),如果推演下去,对于定义域内某个x=x0必然有f(-x0)=f(x0)或f(-x0)=-f(x0),在解决问题中这两种方法有怎样的区别和联系?
例3.已知函数f(x)=(m-1)x2+2x-m2+m是奇函数,求m的值.
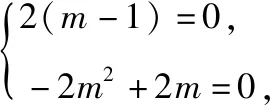
方法2:定义域内任意的x都有f(-x)=-f(x),取特殊值x=0,也有f(-0)=-f(0),则f(0)=0,所以-m2+m=0,则m=0或m=1.
思考:(1)上述两种解法中哪种解法存在问题?给出理由.
(2)比较两种解法的优劣.
【意图】由于所求结果不同,学生容易发现方法2存在问题.方法2中当m=0时,f(x)=-x2+2x,显然不是奇函数,所以m=1.让学生找出理由,给学生一个自由发挥、深入思考的机会.事实上,对于定义域内任意的x,都有等式f(-x)=-f(x),其含义是:每一个x都有一个等式可求得m值,无限个等式求出的m值的公共元素为m=1,所以方法2计算量更小、运算更简便,求得的m值不会丢根,可能产生增根,只要检验即可.
上述问题用定义来求解,无疑是最可靠的,而用特殊值求解,必然让人产生疑虑,所以需要从其真实性上进行推敲,能给学生一个求真的机会、思辨的舞台,更好地培养学生们的理性精神.然而,现实是许多学生并不懂得为什么,只是简单记住这种解法而已,正所谓只知其然而不知其所以然.
三、在方法中提炼模式
从方法的角度,有奇、偶函数的定义域关于原点对称;对于奇函数f(0)=0等,其本质还是奇、偶函数的定义,具体内容是:定义域内任意的x,-x所对应的函数值相等为偶函数,相反为奇函数.表现在图象上,图象关于y轴对称或图象关于原点对称.具体内容与具体图象的融合,就会在学生头脑中产生具体的形象,这些具体的形象会逐渐地嵌入到学生的观念之中.
1.模式的形成
任何解决问题的模式在学生的头脑中形成,都要有孕育、发展和逐渐清晰的过程.作为函数奇偶性定义的运用或推广,下列问题值得思考.
问题:(1)已知函数y=f(x),对于定义域内任意的x都有f(1-x)=f(1+x),则函数y=f(x)的图象有怎样的性质?
(2)已知函数y=f(x),对于定义域内任意的x都有f(1-x)+f(1+x)=4,则函数y=f(x)的图象有怎样的性质?
思考:(1)上述等式是否唯一?如果唯一,请说明理由;如果不唯一,请写出其他等式.
(2)请给出更一般的结论.

2.模式的运用