模型巧引领,高考妙破解
2019-11-19江苏
江苏
韩文美
(作者单位:江苏省张家港中等专业学校)
在解决数学问题时,若能巧妙地构造适当的数学模型,使对应的数学模型与所要求解的问题之间存在着某种特殊的对应关系,进而通过解决对应的数学模型,达到利用相关模型中熟知的数学知识来解决对应问题的目的,方法巧,思路清.
1.构造数或式的数学模型
数或式的数学模型是数学中的一类基本模型,特别是一些相应的有理化因式、对偶式等模型,在破解数学问题中可以起到非常重要的作用.有效构造题目条件中对应的数或式的数学模型,常常能为一些相关问题的破解另辟蹊径,开拓巧解妙证的思维空间.
例1.(2019·江苏卷理·22)设(1+x)n=a0+a1x+a2x2+…+anxn,n≥4,n∈N*.已知a32=2a2a4.
(Ⅰ)求n的值;
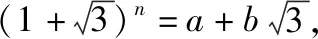
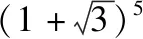
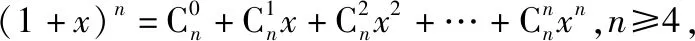
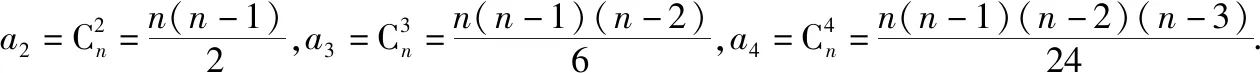
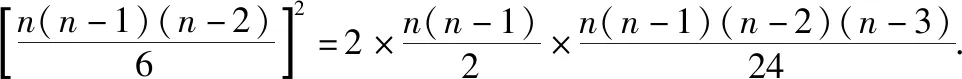
解得n=5.
(Ⅱ)由(Ⅰ)知,n=5.
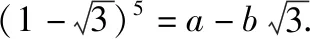
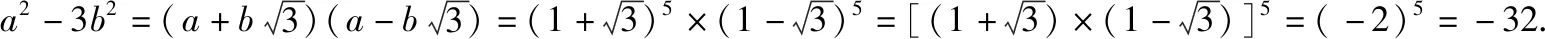
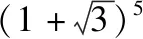
2.构造函数的数学模型
函数的数学模型是数学中最基本的数学模型之一,通过构造特殊的函数模型,可以巧妙破解相关的函数问题、不等式问题和数列问题等,特别是在解决函数的性质与图象、函数值的大小比较和数列的函数性等问题时,特殊函数的构造往往有奇效.
例2.(2019·全国卷Ⅲ·文12理11)设f(x)是定义域为R的偶函数,且在(0,+∞)单调递减,则
( )
分析:根据题目条件构造特殊的函数模型,利用特殊函数来分别计算相应的函数值,再加以比较,避免分析与讨论相应的函数的基本性质,相比更加易于操作.
解析:由于f(x)是定义域为R的偶函数,且在(0,+∞)单调递减,
取特殊函数f(x)=-|x|满足条件,
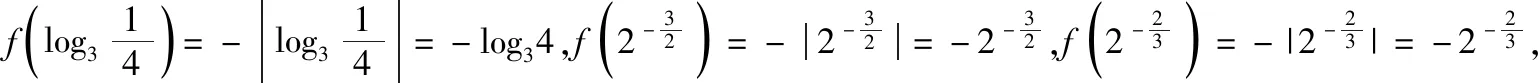
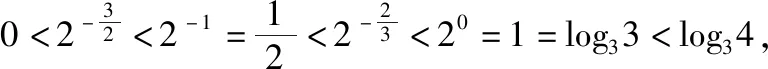
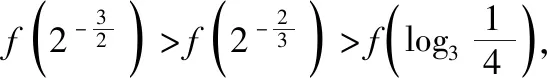
点评:结合题目条件构造与之对应的特殊函数模型——f(x)=-|x|,进而将抽象问题具体化,可以快速准确地解答相关的函数问题,进而得以判断.在解答一些抽象函数、数列的选择题或填空题时,可以选取满足条件的特殊函数模型(一般选择比较常见的基本初等函数,此时基本性质与函数图象较为熟悉)加以验证,变抽象为具体,通过特殊函数发现规律,寻求解答方法.
3.构造方程的数学模型
方程的数学模型也是数学中最基本的数学模型之一,通过构造特殊方程的模型,可以把函数和不等式等问题方程化,借助方程思维,通过方程的判别式、方程的根、方程中的韦达定理等的巧妙转化与应用,破解相应的数学问题.
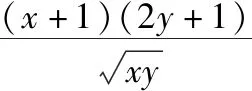
分析:破解此类函数式的最值问题,最常见的思维方式就是借助基本不等式法来处理.而借助相应方程模型的构造,引入参数,再通过方程的转化,结合方程有解的前提条件,利用方程的判别式法加以转化与应用即可.
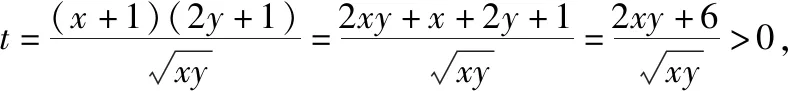
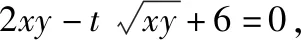
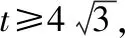
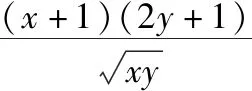
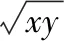
4.构造平面几何的数学模型
平面几何的数学模型是小学、初中阶段比较常见的数学模型之一,而且学生对此有较系统的学习,基础好,借助与问题相关的平面几何模型(常见的有三角形、平面四边形和圆等),特别是一些特殊的三角形、特殊的平面四边形等模型的构造,可以有效解决与函数、不等式、平面向量和解三角形等相关的数学问题.
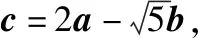
分析:涉及平面向量的夹角问题,往往可以借助平面向量的数量积公式,利用代数运算来处理.而借助题目中平面向量数量积的性质,构造与之对应的平面几何模型——直角三角形,从平面几何的角度入手,结合平面向量的减法运算的几何意义以及解直角三角形问题来确定平面向量中的夹角问题.
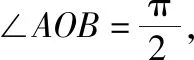
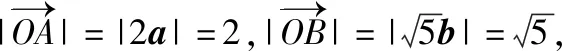
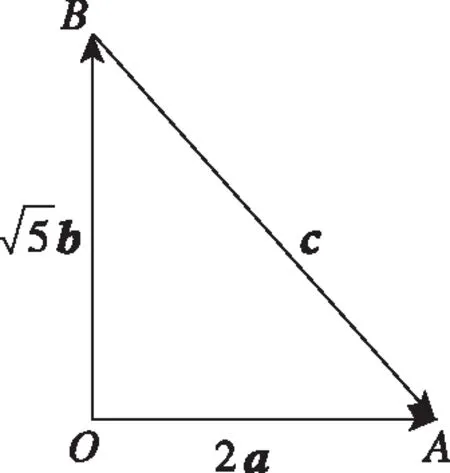
点评:抓住平面向量数量积的性质,以a·b=0得到a⊥b,从而构造平面几何模型——直角三角形,结合平面向量的线性运算、平面向量夹角的定义以及直角三角形的几何性质来确定相应的夹角的余弦值.以“形”化“数”,有效转化,借助几何的直观性,并结合平面几何的性质,可以快捷转化相应的边、角以及最值问题,达到有效、直观、快捷地确定平面向量中的几何量问题的目的.
5.构造立体几何的数学模型
立体几何的数学模型也是小学、初中阶段比较常见的数学模型之一,借助与问题相关的立体几何模型(常见的有长方体、正方体和球等),特别是一些特殊的长方体等模型的构造,可以有效破解与空间几何中的点、线、面的位置关系以及空间距离、空间角度等相关的数学问题.
例5.(2019·全国卷Ⅲ·文8理8)如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则
( )

A.BM=EN,且直线BM,EN是相交直线
B.BM≠EN,且直线BM,EN是相交直线
C.BM=EN,且直线BM,EN是异面直线
D.BM≠EN,且直线BM,EN是异面直线
分析:结合题目条件,直接构造与之相关的特殊长方体模型,进而把该图形放在此特殊长方体模型内,可以确定相应的空间几何中的点、线、面的位置关系以及空间距离等问题的判定与应用.
解析:如图,连接BD,因为点N为正方形ABCD的中心,所以点N为BD的中点,可知直线BM,EN都是在以DB∩DE=D所确定的平面BED内的直线,且不平行,即直线BM,EN是相交直线;
取特殊长方体模型来直观分析,设AB=AD=2,则EC=ED=2,
故选B.
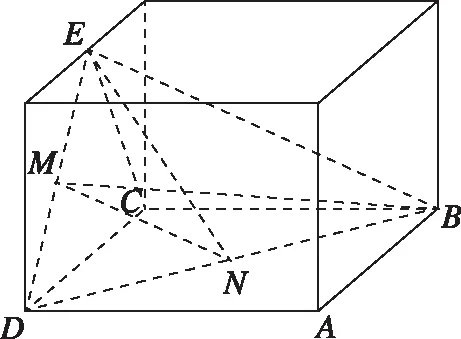
点评:通过特殊立体几何模型——长方体的构造,把一般的问题具体化,为进一步破解空间几何中的点、线、面的位置关系以及空间距离等相关问题的判定提供直观模型,方便判定与求解.特别在研究一些空间中的位置关系、几何量的计算等相关选择题或填空题时,可以根据已知条件巧妙构造特殊的立体几何模型,化一般为特殊来处理.

