以高考视角谈三角函数模块命题趋势
2019-11-19安徽
安徽
朱启州
(作者单位:安徽省淮北市杜集区教育局教研室)
三角函数是重要的基本初等函数,是中学数学的核心内容,长期以来我们常常把它作为一个独立的内容进行教学,同时与平面向量和解三角形小范围进行综合考查,往往忽视将其放到中学数学的大格局里.2017年以前的高考命题确实是这样.2018年全国卷Ⅰ理科第16题,2019年全国卷Ⅰ理科第5,11和20题,2019年天津卷理科第20题等都彰显将三角函数作为普通函数来研究的命题趋势,对高中数学教学有着重要的指导意义.现以近两年高考数学试题为例,谈谈高考数学三角函数模块的命题趋势,供读者参考.
一、三角函数作为普通函数参与新函数构造,拓宽了命题思路
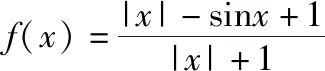
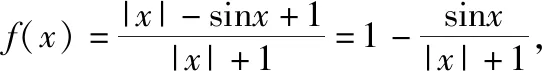
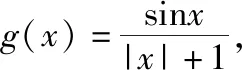
所以g(x)min=-g(x)max,即g(x)min+g(x)max=0.
又M=1-g(x)min,N=1-g(x)max,
所以M+N=2-(g(x)min+g(x)max)=2.
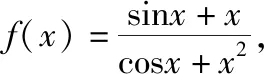
二、命题侧重于考查学生对三角函数概念的理解与性质的综合运用的能力
例2(2019·全国卷Ⅰ理·11)关于函数f(x)=sin|x|+|sinx|有下述四个结论:
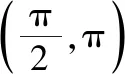
③f(x)在[-π,π]有4个零点 ④f(x)的最大值为2
其中所有正确结论的编号是
( )
A.①②④ B.②④
C.①④ D.①③
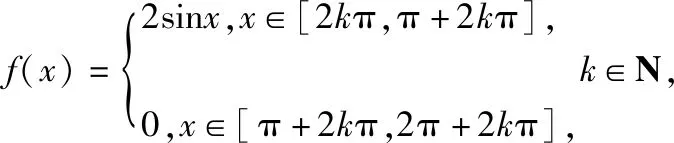
这种在一道选填题中考查三角函数的多种性质的题型,在很多地方高考卷都有体现.本题很好地将不同类型函数的单调性、奇偶性、周期性、函数零点及最值联系起来,它们相互联系互为依据.因此,在教学中应侧重于引导学生对数学的理解,让学生在理解数学的基础上建立各模块知识间的网状联系.
三、综合利用三角函数的图象与性质以及函数求导等数学工具
例3(2018·全国卷Ⅰ理·16)已知函数f(x)=2sinx+sin2x,则f(x)的最小值是________.
解:从本质上讲,此问题是一个与三角函数有关的函数问题,我们可以从函数的单调性、奇偶性、周期性、函数零点、最值及图象等方面入手深入研究.
由f(x)=2sinx+sin2x=2sinx(1+cosx)的最小正周期为2π,所以只需研究f(x)在[0,2π]上的最小值.
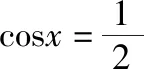

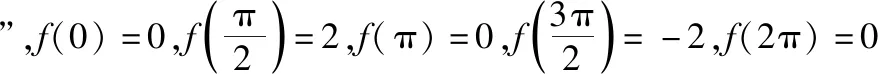
四、解三角形、三角函数与平面向量小范围综合成为考查常态
例4(2019·天津卷理·15)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b+c=2a,3csinB=4asinC.
(Ⅰ)求cosB的值;
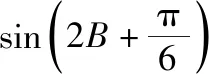
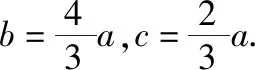
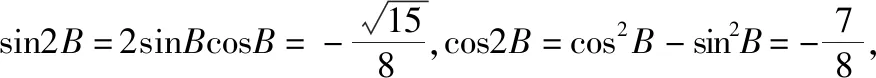
从历年高考试题看,以解三角形、三角函数与平面向量小范围综合作为基础题将成为高考数学命题的常态,重点考查学生对正余弦定理与三角恒等变换的灵活运用.如2019年全国卷Ⅰ理科第17题、全国卷Ⅲ理科第18题和天津卷理科第7、15题等.
五、三角函数的概念、图象、性质和三角恒等变换仍然是备考的超重点
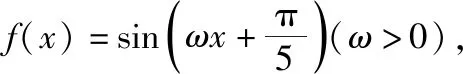
①f(x)在(0,2π)有且仅有3个极大值点
②f(x)在(0,2π)有且仅有2个极小值点
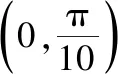
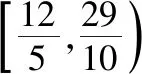
其中所有正确结论的编号是
( )
A.①④ B.②③
C.①②③ D.①③④
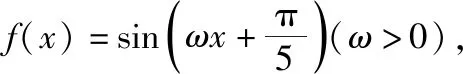
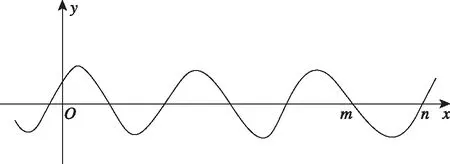
由f(x)在[0,2π]有且仅有5个零点,设其第5、6个零点分别是m,n,

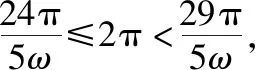
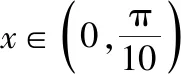
本题重点考查学生对三角函数图象与性质的理解.从2019全国卷命题来看,三角函数的概念、图象、性质与三角恒等变换等传统内容有所削弱,但是由于三角模块概念的基础性和应用的广泛性,这一模块是高中数学的重要组成部分,仍会是今后高考数学命题的超重点,如2019年全国卷Ⅱ理科第9、10题,全国卷Ⅲ理科第12题,天津卷理科第7题等.
六、教学启示

