教学考试杂志社“优师计划”阶段性成果展示——高考重难点相关试题选登

1.已知等差数列{an}的公差为2,S10=50,则a3+a6=

( )

A.0 B.2

C.4 D.6

【答案】D

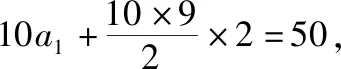
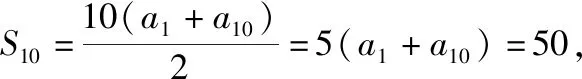
2.已知数列{an},{bn}的前n项和分别为Sn,Tn,且Sn=2n2+3n,2Tn=3bn-3,若两个数列的公共项按原顺序构成数列{cn},则c1=________,{cn}的前n项和Hn=________.(本题第一空2分,第二空3分)

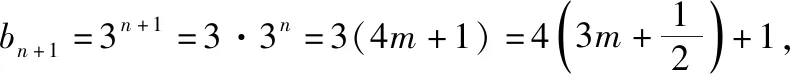
3.意大利数学家斐波那契在32岁时完成了自己的成名作《算盘全书》,58岁再版时增加了著名的“兔子繁殖问题”,即“斐波那契”数列问题,具体数列为1,1,2,3,5,8,…,即从该数列的第三项开始,每个数字等于前两个相邻数字之和.已知数列{an}为“斐波那契”数列,若a2020=t,则S=a1+a3+a5+…+a2019的值为

( )

A.t-1 B.tC.t+1 D.t+2

【答案】B

【解析】本题考查递推数列以及数列求和，考查推理论证能力、化归与转化思想，考查逻辑推理、数学运算核心素养.由题意可得an+2=an+1+an,则a1+a3=a4，a1+a3+a5=a6,a1+a3+a5+a7=a8,……，a1+a3+a5+…+a2019=a2020=t,∴S=t,故选B.

【命题逻辑】数列是高中数学的重要内容，高考主要考查数列的概念以及等差数列、等比数列的概念、性质、通项公式与前n项和公式.其中，等差数列、等比数列的通项公式与求和公式是考查的重点.第一道试题的考查突出基础性，重点考查考生对数列通性通法的理解和应用.而第二道试题为一道多空题，是2019年全国卷Ⅱ文理科首次出现的新题型，通过对题设进行巧妙的设计使其具有一定的综合性，对基础知识的考查和对能力的考查有机结合.试题通过运用等差数列、等比数列的定义推导通项公式，并以公共项构造新数列，重点考查考生对等差数列、等比数列相关知识的理解和掌握.更加考查学生的解题能力，体现了课程标准对数列教学的能力要求.第三道试题是以“斐波那契”数列为试题背景设计新型数列问题.本题重点关注对数学素养的考查，符合课标理念，同时引导考生关注“数学文化”，需要考生有比较强的阅读抽象数学符号语言的能力和一定的逻辑推理论证能力.

( )

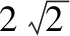
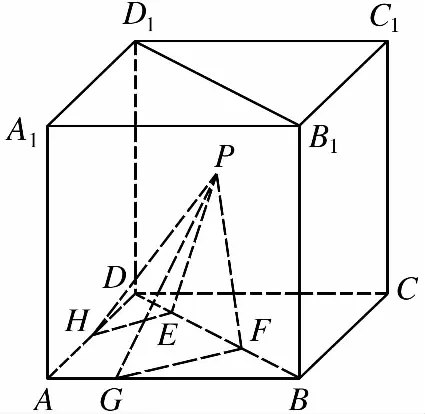
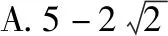
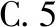
【答案】B

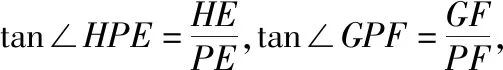
【命题逻辑】立体几何是高中数学的重点内容，在立体几何中，利用空间空间向量将几何问题转化为代数运算，是解决此类问题的一种重要的手段，试题的设计不是简单的基本元素及相互关系，不仅关注了对基础知识的考查，更重视了对数学能力的考查，试题的设计对考生的空间想象能力要求较高，综合考查考生的空间想象能力、推理论证能力和运算求解能力.试题的设计源于教材且高于教材.