求解信赖域子问题的改进变步长休恩算法
2019-11-18张春霞王希云
张春霞,王希云
(太原科技大学 应用科学学院,太原 030024)
无约束最优化[1]问题如下:
minf(x),x∈Rn.
(1)
其中f(x):Rn→R是目标函数,x∈Rn是待求变量。
信赖域方法是在非线性优化问题[2]中备受关注的一类算法。当用信赖域方法求解无约束最优化问题时,关键在于每步迭代时都需求解下面形式的二次模型[3]信赖域子问题:
(2)
当Δ变化时,上述二次模型信赖域子问题的解δ*形成一条空间曲线,称为最优曲线[4]。
目前求解信赖域子问题的算法很多,当Hessian正定时,折线法相对好些。常用的方法有单折线[5]、双折线[6]、切线单折线[7]等。
2015年王希云、于海波提出了一类R-K类算法[8],一种变步长的休恩算法(CH)[9]。R-K类算法的基本思想是利用R-K类方法构造一条折线进而代替最优曲线来求解信赖域子问题。2017年王希云、贾新辉提出了改进的显示欧拉、隐式欧拉、平均欧拉[10-11]求解信赖域子问题。本文在于海波和王希云提出的变步长休恩方法的基础上,改进了繁琐的步长形式,提出了一种改进的变步长休恩算法(ICH)。
本文为简化步长形式,将文献[9]的假设条件修正为:
(3)
算法步长简化为:
(4)
hn=
(5)
其中n=0,1,2,l,N-1,δ0=-B-1g,ε称为限制步长,即限制每步步长的最大值只能达到ε.限制步长ε越小。
数值实验表明改进后算法的迭代次数更少、计算时间更短。
1 算法
下面给出我们改进的变步长休恩算法的具体步骤:
步1 给定梯度g,正定矩阵B,信赖域半径Δ.
步2 令δ0=δnp-B-1g,如果‖δ2‖2≤Δ,则取δ*=δ0.停止计算,否则转步3.
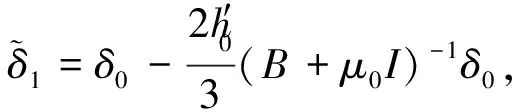
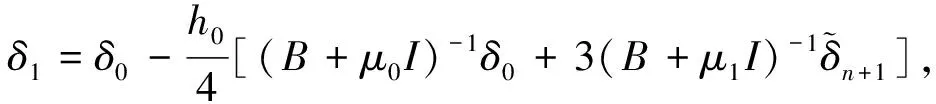
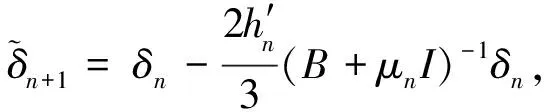

停止计算,否则令n:=n+1,转步5.
2 改进的变步长休恩折线路径的性质分析
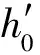
① 当n=0,1,2,…,N-1时,则:
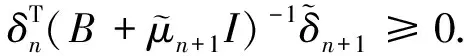
② 当n=0,1,2,…,N-1时,则:
证明①当n=0,1,2,…,N-1时,
(B+μn+1I)-1δn
又由式(4)可得:
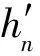
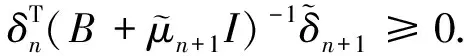
证明② 当n=1时:
因为

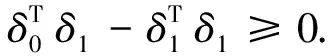
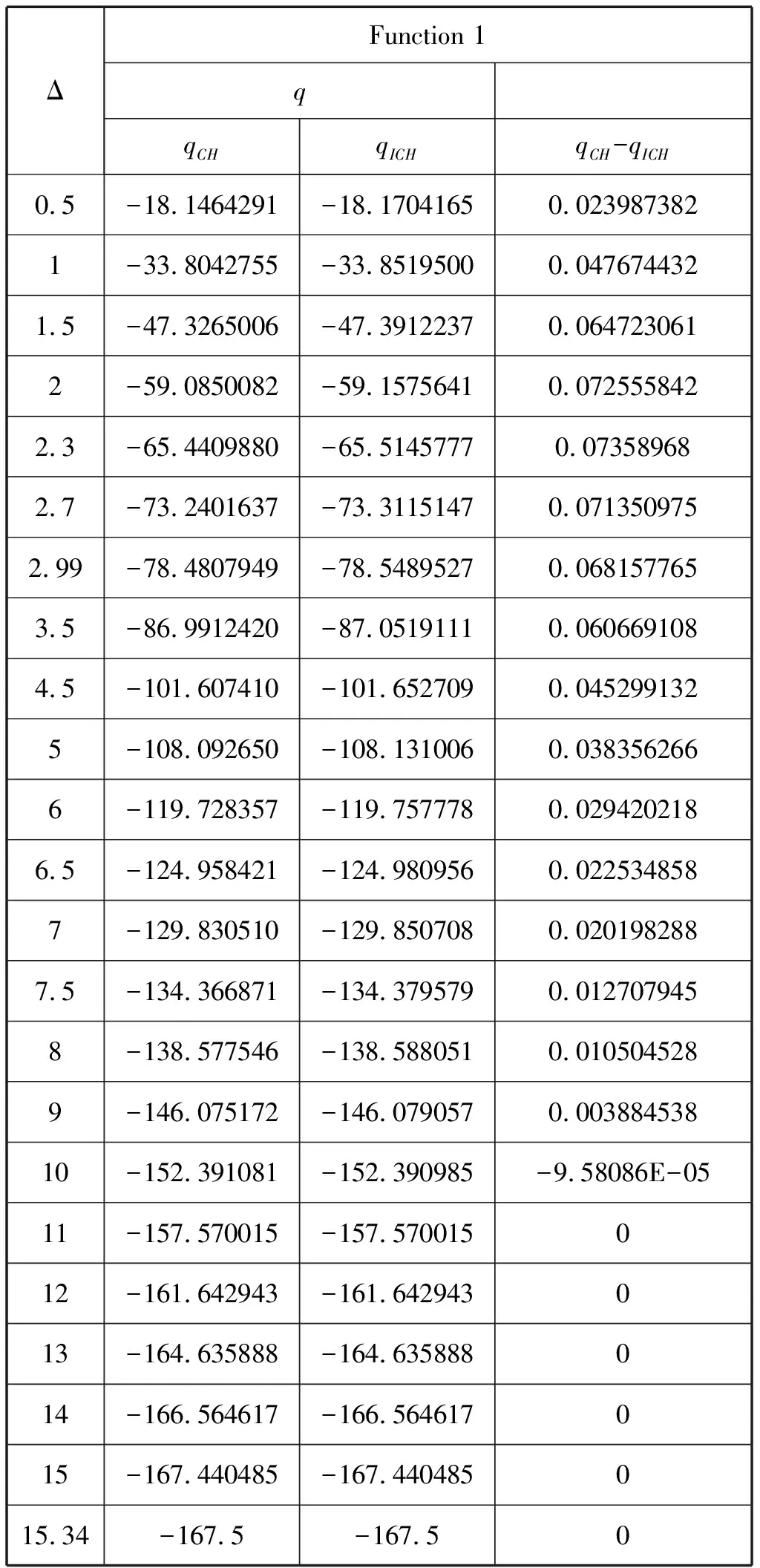
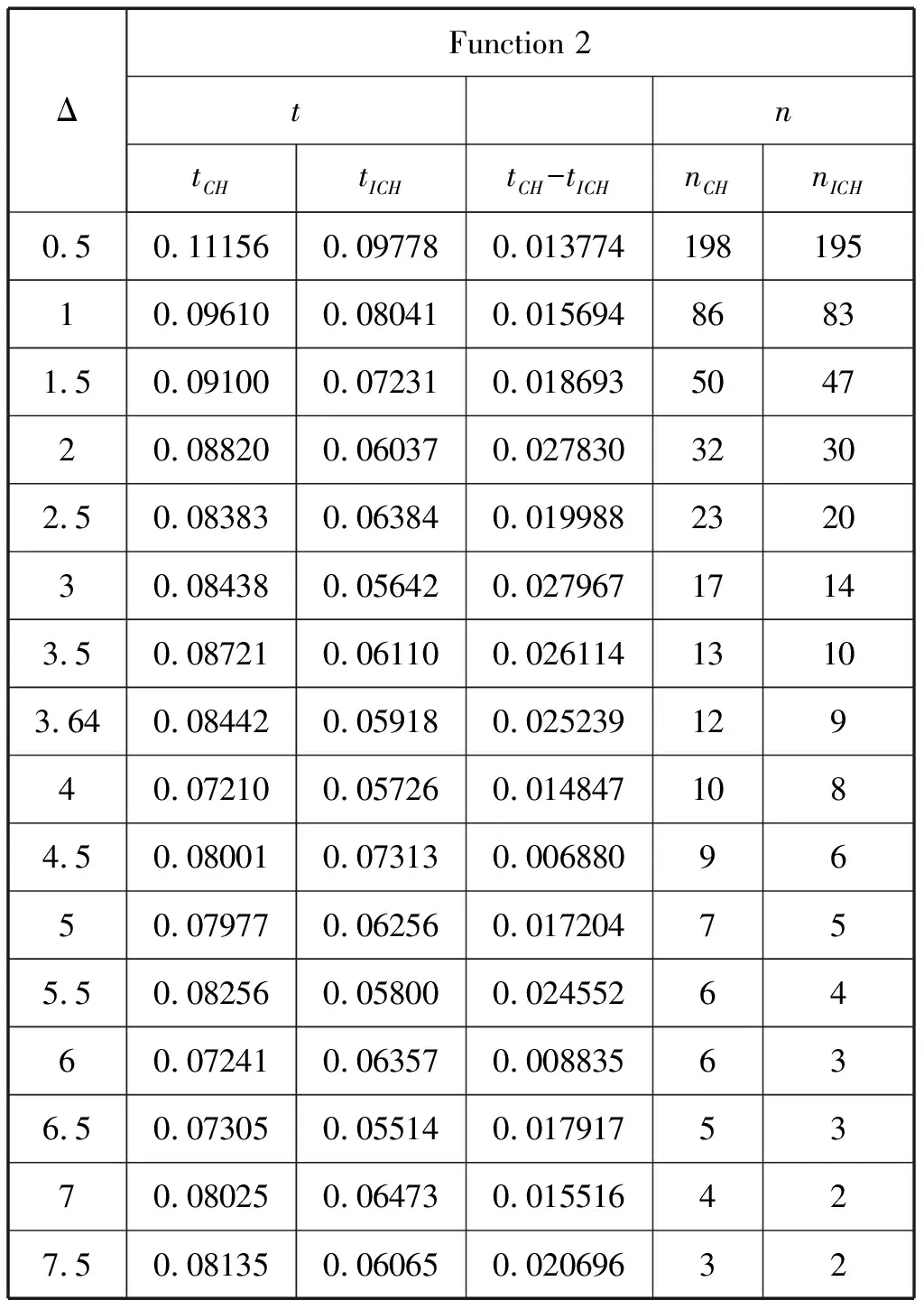
假设1 则当n=k+1时: 又由: 可得: 则: 且: 故由第二数学归纳法可知原命题成立。 定理设B对称正定,且当n=0,1,2,…,N-1时有下式成立, 则δ(τ)满足如下要求: ①‖δ(τ)‖2关于τ为单调非增函数; ②q[δ(τ)]关于τ为单调非减函数。 证明:① 当τ∈[β0,β1],即τ∈[0,h0]时 则: 因为: 故‖δ(τ)‖2在区间τ∈[β0,β1]上为单调非增函数。对∀τ∈[βi,βi-1],即:(τ-βi)∈(0,hi),n=0,1,2,…,N-1时: 则: 由式(5)可知: 所以 故‖δ(τ)‖2在区间(βi,βi+1),n=0,1,2,…,N-1上都为单调非增函数。 ② 当τ∈[β0,β1],即τ∈(0,h0)时: 则: 所以q[δ(τ)]在区间[β0,β1]上为单调非减函数。 对∀τ∈[βi,βi-1],即(τ-βi)∈(0,hi),n=0,1,2,…,N-1时: 则: 故q[δ(τ)]在区间[βi,βi+1],n=0,1,2,…,N-1上都为单调非减函数。 改进的变步长休恩算法与改进前算法做对比,t表示求解子问题所用的时间,n表示迭代次数,q表示测试函数的最优解的函数值。 对于测试函数Function1,数值实验结果[12]如表1和表2所示,当信赖域半径较小时,本文提出的改进的休恩三阶算法要比原算法的计算速度快,迭代次数少,且在计算结果的精度上与之相近。对于测试函数Function1,当信赖域半径0.5≤Δ≤10时,改进的变步长休恩算法求得的信赖域子问题的最优值要比原算法的好,当Δ接近‖δnp‖2时,两种方法求得的结果一样。对于测试函数Function2,数值实验结果[12]如表3和表4所示,当信赖域半径0.5≤Δ≤8时,改进的变步长休恩算法求得的信赖域子问题的最优值要比原算法的好,当Δ接近‖δnp‖2时,两种方法求得的结果一样。因此本文提出的改进的休恩三阶算法可以很好的近似最优曲线,且比原算法的迭代次数少,计算时间短,是有效可行的。 表1 测试函数1的数值结果Tab.1 Numerical results of test Function 1 表2 Function 1的运行结果Tab.2 The running of Function 1 表3 测试函数2的数值结果Tab.3 Numerical results of test Function 2 表4 Function 2的运行结果Tab.4 The running of Function 2 ΔFunction 2tntCHtICHtCH-tICHnCHnICH80.071240.060700.0105402290.061130.059260.00187100100.061130.052670.00846000110.052530.038150.01438000 测试函数: Function 1 s.t.‖δ‖2≤Δ. Function 2 s.t.‖δ‖2≤Δ.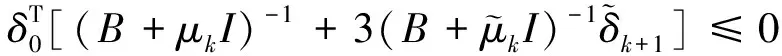
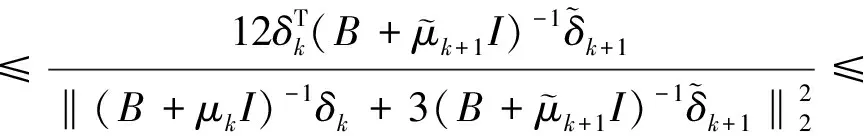

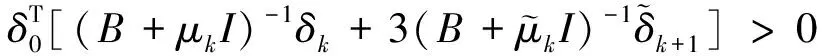
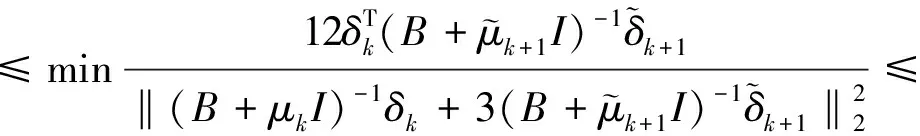

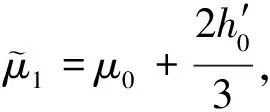
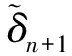

3 数值结果