高阶全变差正则化彩色图像去马赛克
2019-11-18刘铭丽王希云
刘铭丽,王希云
(太原科技大学 应用科学学院,太原 030024)
随着数码摄(照)像机等电子产品的普及,去马赛克逐渐成为高质量图像采集与处理中必不可少的关键。
彩色图像去马赛克的过程可以建模为清晰图像与马赛克算子的卷积,再加上噪声,从由观测到的加马赛克图重构清晰图的过程即:
a=A⊗x+n
(1)
式中,⊗表示卷积算子;a为观测到的加马赛克图像;x为待复原的原始图像;n为噪声。由于随机噪声的存在,因此图像的去马赛克问题是一个不适定问题[1],通过引入正则化项来克服病态。 一般通过引入正则化项来克服病态。因此,常常采用正则化方法建模为如下的最小化模型进行求解:

(2)
其中:第一项为数据保证项;第二项为正则项;μ1为正则化参数,用来控制保真项与正则化项之间的加权比例。
1992年由Rudin,Osher和Fatemi[2]提出了总变分TV极小化方法用于解如下极小化问题:

(3)
2014年Laurent Condat[3]将彩色图像去马赛克表示成离散总变分模型为:
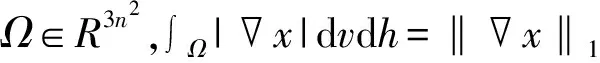
为了克服由全变分(TV)正则化所产生的阶梯现象,学者们提出了相应的解决方法[4-8],其中采用高阶范数来度量图像就是一种有效的方法。
1 模型的建立
彩色图像去马赛克问题不仅与该像素点水平和竖直两个方向像素有关,还应该与正对角线和负对角线方向的像素有关,而高阶变差正则化[9]正是考虑了多个方向像素值的影响而建立的图像复原模型,其在局部小范围内利用二次曲面函数逼近图像函数,所以不会出现上述“阶梯”现象[9-12],为了克服一阶变差利用一次平面函数逼近图像函数的缺点且提高图像去马赛克质量,借鉴高阶变差方法的优点,本文提出了一种高阶全变差正则化彩色图像去马赛克模型。
通过引入四阶PDE提出如下的能量函数:

(5)
1.1 正则化项的离散化
定义一个二阶向量微分算子[13]:
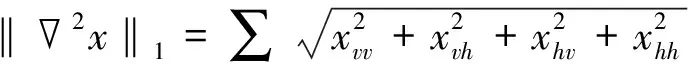
式中:xvv,xvh,xhv,xhh分别代表图像函数x离散以后在水平方向、正对角线方向、负对角线方向和竖直方向的二阶差商。设图像大小为N×N,选择周期边界条件,在像点位置(i,j)处:
利用矩阵D代替二阶向量微分算子2,即令
1.2 模型的离散化形式
综上,在离散化形式中能量函数(5)可写成如下形式:

(6)

2 模型的求解
原始对偶不动点算法(PDFP)是求解图像非光滑凸优化问题的一种有效算法,其变量是全分裂的,参数容易选取,因此适用于数量级较大的模型问题。所以本文考虑采用PDFP[14-15]求解该模型。
对于目标函数:
(7)
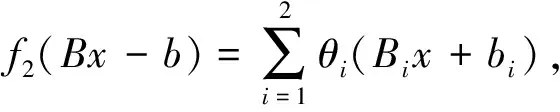
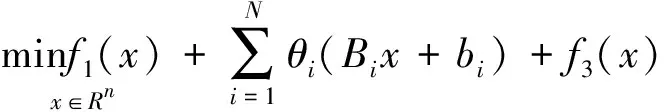
(8)

对于目标函数(7)PDFP[14-15]求解步骤如下:
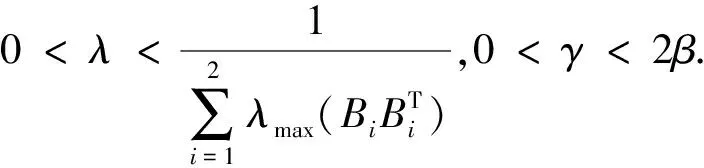
若取:
θ1=μ1‖·‖1,B1=D,b1=0
f3(x)=0
则求解模型(5)的PDFP的步骤为:

3 数值实验
为了验证本文提出的彩色图像去马赛克模型的有效性,以Matlab2015a编程为工具,实验数据采用7幅像素大小为500×500的彩色柯达图像(Kodak PhotoCD dataset)。在实验进行之前,首先对去马赛克模型中涉及到的重要参数的设置进行说明,μ1控制高阶TV扩散的速度,因此本文实验中取μ1∈[0.0,1.0],以0.10为步长,从得到的复原结果中选择最好的结果对应的μ1作为实验最终取值,即分析图1选取了恰当的参数值。为了更好地比较去马赛克后的细节信息,且考虑到篇幅影响,用框选出了两幅彩色图像的局部作为实验对比所用的部分,如图2所示。实验分别从图像恢复的视觉效果以及峰值信噪比(CPSNR)来主客观地评价所提出模型的性能。

图1 μ1值对实验结果(CPSNR)的影响Fig.1 The influence of μ1on experimental results


图2 彩色图Fig.2 Color image

图3 实验结果对比图Fig.3 Collation map of experimental results
主观上,图3中(a)、(b)从左上角到右下角分别为:原图、加马赛克图、ROF模型以及本文模型结果图。从图3可以看出ROF模型的实验结果出现了阶梯现象导致图像模糊,由于此模型为二阶PDE是通过最小化图像梯度的能量函数得到的,能有效保持边缘但是在平滑区域容易出现阶梯现象。而本文的模型用四阶范数来代替TV范数,四阶PDE是最小化图像拉普拉斯变换的能量函数,因此能在图像的光滑区域消除阶梯现象,从而使得去马赛克后的图像细节部分更接近原图。
客观上,为了检测图片还原质量的好坏,采用峰值信噪比[16](CPSNR)作为图片质量的评价标准,CPSNR可描述为:
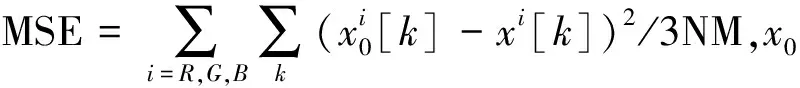
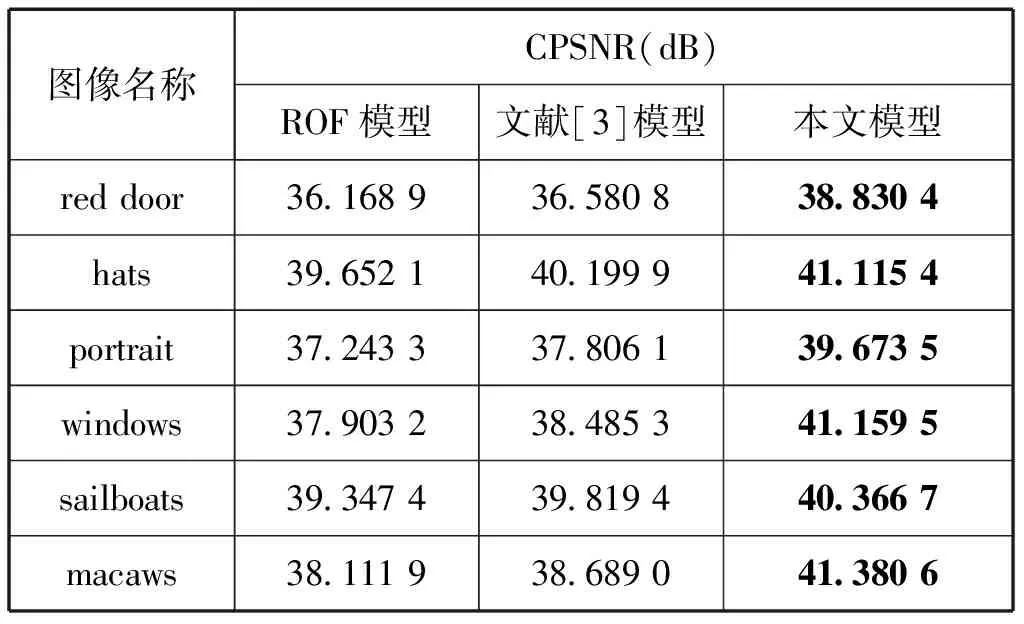
表1 图像恢复结果的信噪比CPSNRTab.1 The CPSNR of image restoration results
表1分别表示ROF模型、文献[3]模型以及本文模型结果的CPSNR值,从表1(黑体表示较好的效果)比较结果可以看出本文模型的每幅图像的CPSNR值都比ROF模型高约1.5~3 dB.主观和客观评价都显示了本文模型的优越性。
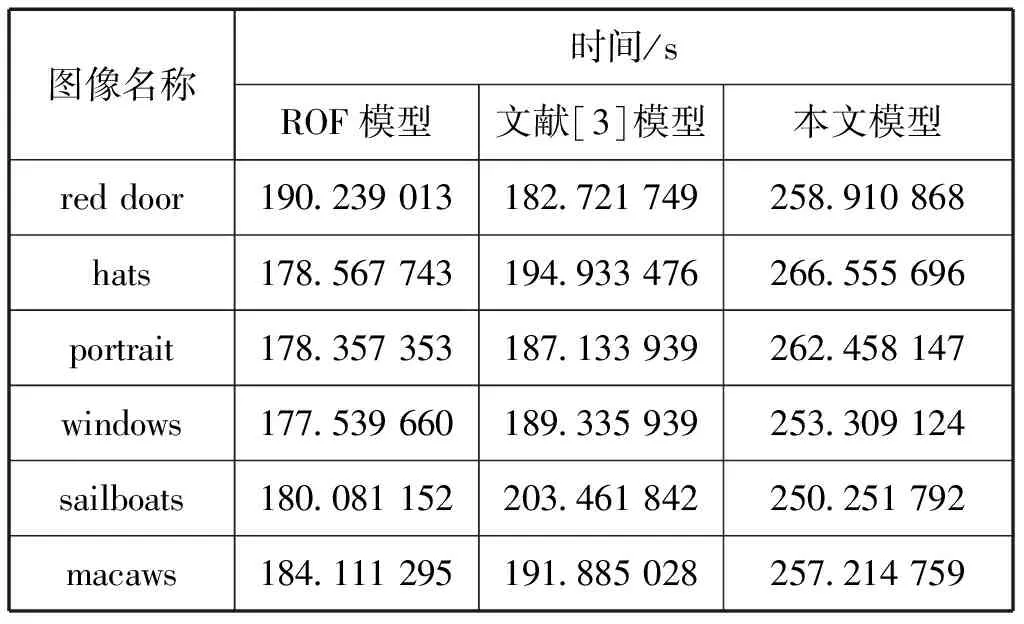
表2 图像恢复所用时间Tab.2 The time of image restoration
表2分别表示ROF模型、文献[3]模型与本文模型图像恢复所需的时间,因为相比于二阶范数,四阶范数多了求导数的过程,因此所需时间相比二阶要久一些,这也是之后工作在算法部分需要改进的地方。
4 结语
本文在ROF模型的基础上,引入一个四阶PDE来度量图像,用四阶范数来代替TV范数,克服了采用TV模型去马赛克所产生的阶梯效应,实验结果表明,该模型能获得较好的去马赛克效果。进一步的工作是提高算法的计算速度,以便能够更好地应用于实践。
