基于二维变分模态分解的矿井图像增强方法

贾 焕,杨铁梅,李琴琴

(1.太原科技大学电子信息工程学院,太原 030024;2.太原理工大学工程训练中心,太原 030024)

由于煤矿井下存在光线较弱、粉尘大等恶劣情况[1],导致摄像机采集回来的视频图像清晰度差,而且在图像转换和传输过程中的操作不当也将导致图像的质量下降[2],因而增加了对主皮带裂缝边缘进行提取和检测的难度。在处理传送带跑偏等问题时也遇到同样的问题。所以急需进行煤矿井下图像增强处理。

近年来,针对低照度和多粉尘的图像问题,许多学者提出了不同的方法,有传统图像增强方法、基于Retinex算法及其改进方法等。最常用的传统方法有灰度变换法和直方图均衡化[3],这两种方法效果都不错,但是对彩色图像极易引起图像失真,如像素点过饱和引起的图像结构的破坏。Retinex算法及其改进方法适应范围广、计算精度高。李大军等[4]通过参数估计进行自适应双边滤波,但高频噪声去除问题没有得到解决。胡韦韦等人[5]提出了基于双边滤波的Retinex图像增强算法,该算法采用双边滤波代替高斯滤波来估计光照,能够有效抑制光晕和色彩失真现象,但算法复杂度高,无法实现实时处理。曹伟等[6]采用边缘检测加权引导滤波进行指静脉图像增强,能够清晰保存图像的纹理细节,但是参数过多,并且没有给出参数估算的方法。因此本文提出一种基于加权引导滤波的二维变分模态算法来处理煤矿主皮带图像以改善图像质量。

1 相关理论

1.1 引导滤波

引导滤波[7-8]原理简单、在突出边缘细节的同时提高图像质量,其滤波半径与灰度值范围无关,滤波时间仅仅依赖图像总像素,因此广泛应用于降噪、抠图和HDR压缩等领域。它不能在减少噪声的同时提高边缘细节,而且当图像灰度数值变换过快时有可能出现假性边缘。因此,需要增强边缘特性。本文将自适应正则化因子与区域方差信息相结合,对正则化因子进行加权以突出图像边缘细节纹理,用来改善原引导滤波的缺陷。

根据引导滤波算法,设引导图像为I,预处理图像是P,结果图像为q,局部线性模型如下:

qi=akIi+bk;∀i∈ωk

(1)

其中:ωk表示以像素i为中心的邻域,半径大小为k的一个邻域,其中ak和bk是窗中心为k的固定值。对式(1)进行求梯度得:q=aI

当引导图像有梯度时,输出图像也必须有,这是局部窗口ωk(1)成立的基本条件,也是引导滤波能保持边缘的重要原因。

为求解(ak,bk)的最优解,也是拟合输出函数与原图像的最小化,则需要对下式代价函数求解

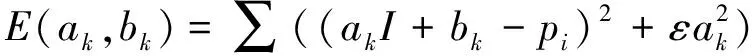
(2)

其中:第一个部分是二次保真度项,它确保建立局部线性模型,同时最小化p与q的差异; 第二项是常规项,用于调节数值过大。当它等于0时,前导图像为当前滤波图像时所获得的普通解,因此ε必须大于0.

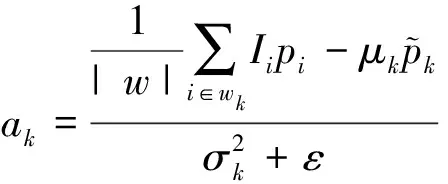
(3)

(4)

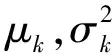
(5)

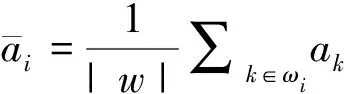
由于引导图像和待滤波图像之间的线性关系,当引导图像指向待滤波图像的边缘时,图像的边缘细节就会显示。

1.2 二维变分模态分解(Two-Dimensional Variational Mode Decomposition,2D-VMD)

2D-VMD是一种新的自适应变分方法,它将图像分解成几个不同且独立光谱波段的模式。2D-VMD在经验模式分解算法的基础上进行了扩展,具有很高的非递归性、完全自适应性,并且它在图像增强和去噪方面都得到了很好的发挥。其详细的分解过程可参考文献[8-11]。

现在将结合所有广义2D-VMD特征来定义变分模式分解的二维扩展。其函数最小化为：

(6)

其中:{uk}={u1,…,uk},{wk}={w1,…,wk}

用式(6)作为评价模态带宽的目标函数。目标函数是模式带宽之和的评估,仅具有半空间频率,通过与当前中心频率估计的复指数混合而移位到基带,同时保持重建信号的相似程度。

重建约束通过二次惩罚函数和拉格朗日乘子来解决,并且采用乘法算子交替方向法优化2D-VMD.二次惩罚函数和拉格朗日乘数可以约束保真度,使问题不受限制,将约束变分问题转换为非约束变分问题,因此扩展拉格朗日表达式为:

L({uk},{wk},λ):=

(7)

∀w∈Ωk,Ωk={w|〈w,wk〉}

(8)

同样在频域式(8)可改写为

(9)

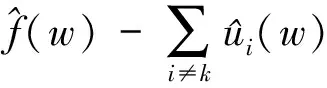
1.2.1 计算过程

在更新完频域数据之后,对傅里叶函数求逆,得到最后的结果。BVMD算法的优化过程如下:

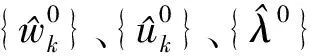
B)根据式(8)和(9)在频域内更新wk、uk

C)更新λ,其中

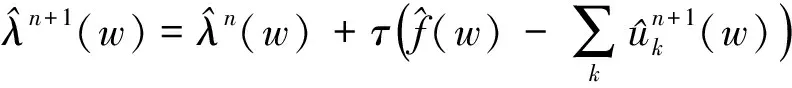
(10)

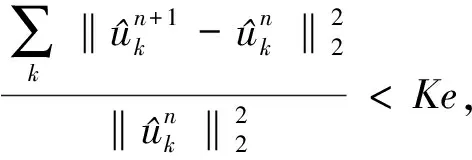
由于模式被有意识地分离并且窄带化,因此该频谱非常适用于分割。合成图像的分辨率是256×256,实验参数以ak=1 000和ke=5运行。

2 基于加权引导滤波同步去噪的二维变分模态算法

2.1 高频分量去噪

噪声能量大部分存在高频带中,二维变分模式分解算法可以分解到不同频率的高频模式,利用自身的维纳滤波器进行降噪,通过对高频子模态内容的抑制和重建,以达到消除高频噪声。

2.2 低频分量增强

信号和图像的主要能量集中分布在低频区域。为了达到图像增强的目的,本文将2D-VMD保留的低频子模态进行加权引导波滤波。

采用引导滤波进行主皮带图像增强无法对主皮带的细节特征提取和剖析。因而需要对主皮带图像进行边缘预估。

常用的边缘检测算子有Sobel,Canny,Gaussian和 Laplacian[11]等,Canny算子的细节检测效果优于其余算法,具有较强的降噪能力,因此本文选用Canny算子进行边缘参数幅值估计。

2.3 边缘预估

Canny方法[12-13]应用保留边缘的选择性模糊自适应中值滤波剔除高频噪声,利用Sobel算子进行像素点梯度强度和方向的计算,应用非极大值抑制得到准确的响应,最后根据Otsu算法自适应生成高、低双阈值来提取边缘信息。

Canny算子进行边缘参数幅值估计之后,对固定正则化因子进行惩罚,并分别得到边缘区域和平滑区域的自适应正则化因子。因而式中的代价函数定义为:

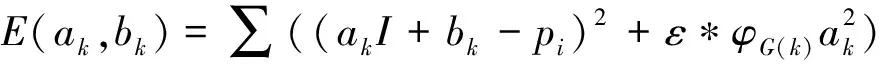
(11)

式中φG(k)是引导图像边缘强度,定义为

φG(k)=∑Icanny(x,y)*(Nsize+l)

(12)

其中,Icanny(x,y)是图像I经过Canny算法检测之后的边缘像素。Nsize为图像中所有像素个数,l=(0.001τ)2,由于灰度图像深度为8,所以τ取值256.

2.4 计算过程

1)对图像进行灰度化处理,因为煤矿下光线 单一,灰度化可以提高处理的效率;

2)对灰度化图像进行canny处理,计算边缘加权值;

3)采用2D-VMD对预处理的图像进行一系列的变分模式分解;

4)保留2D-VMD处理后的第一张图像进行加权引导滤波处理;

5)对处理好的图像进行客观分析和总结。

3 实验结果和分析

3.1 主观评价

通过人眼观察一系列有关联的图像,做出合理的评判,是主观评价最常用、最直接的评价方式。本文通过对多组数据进行验证之后选择其中三组图像作为仿真对象,以使该算法的结果更具说服力,同时验证算法的有效性。

图1 仿真对象Fig.1 Simulation object

图2中的3类图像分别为自适应双边滤波算法、加权引导滤波算法、本文算法图像增强结果如图2至图4所示。

这三组照片光照度不够,图像质量不高。从实验结果可看出:自适应双边滤波算法虽然使得图像在亮度方面比原图提高很多,但是却存在过饱和、过亮问题、光晕移影和对比度低现象;加权引导滤波算法使整体亮度和边缘细节有所改善,但噪声敏感度较高、信噪比低;本文所提的算法(改进的二维变分模态算法)在图像亮度、对比度和细节方面都有不错的效果,图3不仅增强了整体图的亮度,而且把原本在暗处的两辆车突显出来,图4小女孩的头发更加真实,车窗上所倒映的环境清楚,色彩饱满,比前两种算法视觉更好。

图2 矿井主皮带图像增强结果图Fig.2 Iimage enhancement resultgraph of mine main belt

图3 夜景图像增强结果图Fig.3 Image enhancement result graph of night scene

图4 girl图像增强结果图Fig.4 Girl image enhancement result graph

3.2 客观指标评价

图像处理中算法的优劣性以及对算法的性能评价将决定算法的可靠性和准确性。客观指标可以对算法的结果进行更为客观、科学的分析。峰值信噪比(PSNR)和归一化均方误差(NMSE)都是信号重建质量评价最常用、科学的方法。对于参数 PSNR 来讲,其PSNR值与图像失真成反比例现象,数值大则失真越小,图像质量越好; NMSE反映的是当前图像和参考图像之间的均方误差,NMSE值越小,图像越有研究的必要。其定义如下:

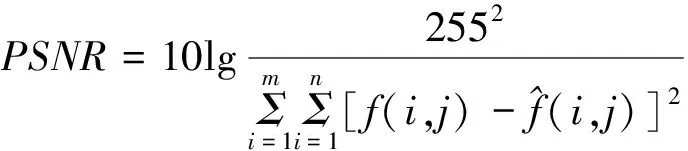
(13)

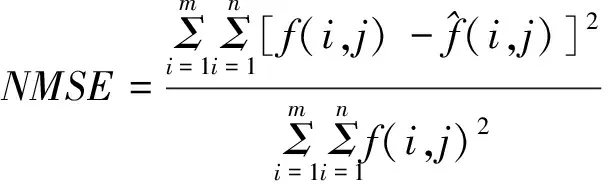
(14)

对自适应双边滤波、2D-VMD下的自适应双边滤波、加权引导滤波算法和本文算法进行分析比较,其结果如下:

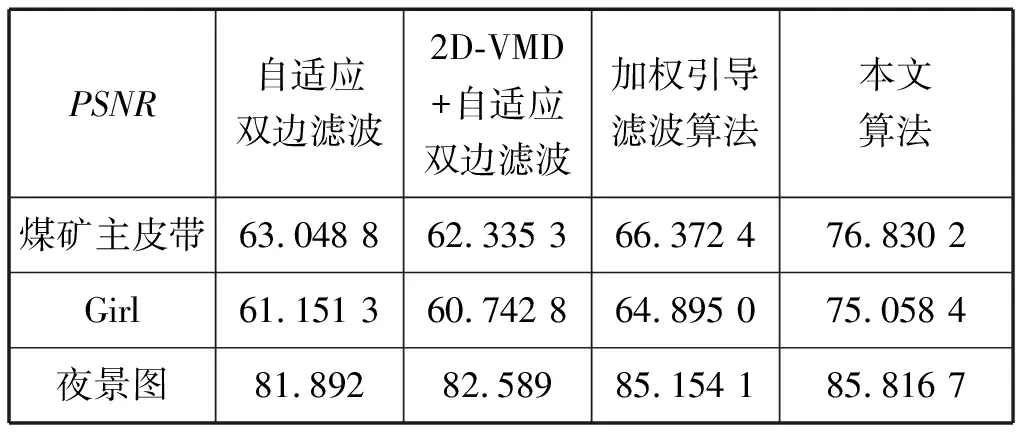
表1 本文算法与其他算法的PSNR客观分析对比Tab.1 Objective analysis of PSNR betweenthis algorithm and other algorithms

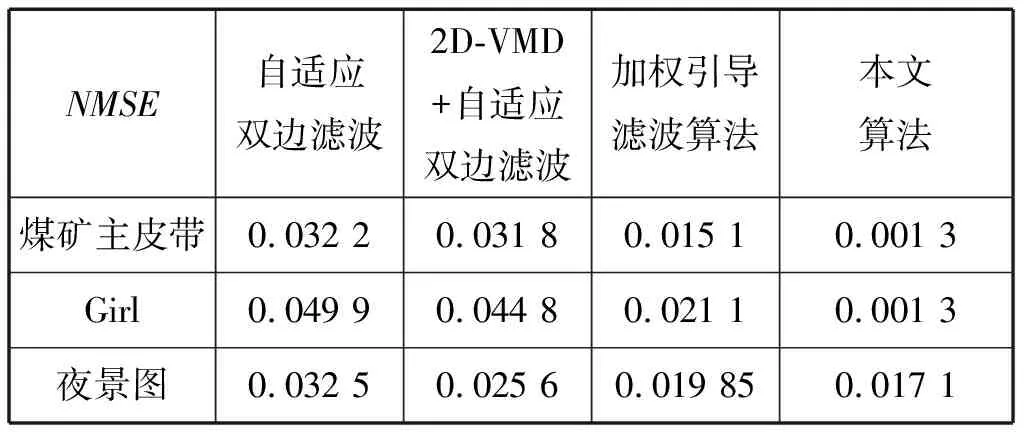
表2 本文算法与其他算法的NMSE客观分析对比Tab.2 The objective analysis of NMSE betweenthis algorithm and other algorithms

由表1可见,本文算法中煤矿主皮带的峰值信噪最高,说明图像失真度小,与其他算法之差为10.457 8～13.781 4;Girl的PSNR数值最高,与其他算法相差10.163 4～13.907 1;夜景图数值较高,相差范围在0.665 3～3.924 6.同理在表2中可以看出本文算法的NMSE数值较低,研究的价值较高,因此更加凸显了算法的优越性。

4 结论

本方法将加权引导滤波边缘细节平滑算法用于二维变分模态分解的低频子模态中,使得预处理图像在边缘强度估计下,更有效突出细节边缘,其次二维变分模态算法的维纳斯滤波器有效的去除高频噪声,使得煤矿井下图像清晰。从主观和客观两个方面评价图像质量,图像视觉效果好,评价指数高。因此该算法可有效突出边缘细节,克服图像高频噪声的缺点,使图像轮廓更清晰,图像更平滑,质量更高。