高速列车脱轨监测关键算法研究
2019-11-16艾永军陈春俊熊仕勇张振
艾永军 陈春俊 熊仕勇 张振

摘要:基于轨道不平顺检测技术的发展,根据轮轨几何关系脱轨理论,设计一种能够工程实施的脱轨监测方案,采用轮轨横向、垂向相对位移近似替代轮对接触点位移和车轮抬升量来判断列车脱轨。针对测控方案中关键参数轴箱振动位移测量困难、测量误差大的问题,使用卡尔曼滤波设计一种估计算法,实时计算轴箱横向、垂向位移;观测噪声方差变化会导致卡尔曼滤波发散,采用小波变换在线估计噪声方差,提高卡尔曼滤波算法鲁棒性。仿真表明:该算法能够通过加速度信号精确计算轴箱振动位移,误差在10%以内,为高速列车脱轨在线监测提供一种思路。
关键词:高速列车;安全性;脱轨监测;卡尔曼滤波;小波变换
中图分类号:U229 文献标志码:A 文章编号:1674-5124(2019)10-0109-05
0 引言
随着复兴号的正式运营,中国高铁最高时速已达400km/h。高速列车的安全运行是提速的基本前提,目前列车运行安全性由脱轨系数、轮重减载
收稿日期:2019-02-17;收到修改稿日期:2019-03-18
基金项目:国家自然科学基金资助项目(51475387)
作者简介:艾永军(1992-),男,安徽芜湖市人,硕士研究生,专业方向为高速列车自动化控制与检测。
通信作者:陈春俊(1967-),男,四川蒲江县人,教授,研究方向为高速列车测试、诊断与控制等。率等指标衡量,主要方法是使用测力轮对测得轮轨力进而计算脱轨安全性指标来评判列车安全性[1]。但由于测力轮对维护困难,并不适用于高速列车脱轨的在线监测[2]。
列车脱轨在线监测是轨道交通领域研究的难点和热点之一。近年来,为实现高速列车脱轨在线监测,国内外学者对此进行了大量探索。日本学者城取岳夫等[3]在转向架上安装加速度传感器,将采集到的加速度数据与预先建立好的加速度统计特征数据库数据进行对比,依据振动加速度的波形特征判断是否脱轨,但数据库建立难度大。唐永康[4]通过位移传感器、加速度传感器,实时检测车轮与钢轨的横向与垂向相对位移、作用力和车轮加速度,通过综合判据来监测车辆脱轨。轮轨相对位移可以反映车辆运行安全状态,钟莎[5]将摄像机固定在转向架上,通过图像处理的方法计算轮轨相对位移,以实现列车安全运行监测目的,但忽略了构架与轮对之间的相对振动。
随着我国轨道不平顺技术的发展,本文旨在基于轨道不平顺检测技术基础上对列车脱轨进行监测。王卫东[6]采用激光摄像机研制的GJ-6型轨道检测系统,提高了系统处理速度,最高达到400km/h检测要求。熊仕勇[7]基于数字激光测量和惯性测量研制的轨道不平顺检测系统,检测误差在1mm以内。
基于轨道不平顺检测技术,提出一种通过轴箱上安装加速度传感器监测列车脱轨方案,使用卡尔滤波设计脱轨监测关键算法,并通过小波变换对算法进行优化。建立了动力学仿真模型并获得数据,验证算法的正确性。
1 轮轨几何关系判断脱轨原理
1.1 车轮抬升量判断脱轨原理
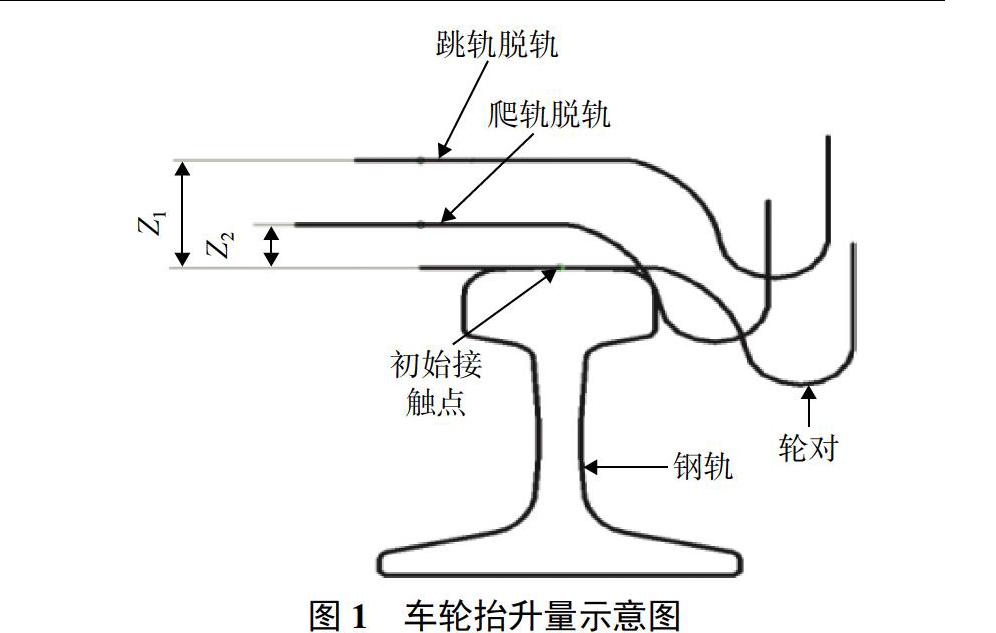
针对脱轨指标在某些情况下不能准确反映列车脱轨状况,翟婉明等[8]提出了一种车轮抬升量判定脱轨原理。列车脱轨表现为车轮脱离钢轨,直接从轮轨几何关系来判断车辆脱轨是一种可行的方法。车轮抬升量定义为车轮踏面名义接触点与钢轨顶面最高点的垂向距离,其原理如图1所示。
只要车轮抬升量小于轮缘高度,理论上车轮尚未摆脱钢轨约束。因此以轮缘高度为临界点,采用车轮抬升量判断车辆脱轨与否,可表示为
Z1,2
在计算机仿真计算中,系统需要进行离散化,针对本文处理问题,离散状态空间方程可表示为
Xk=FXk-1+Gvk
Zk=HXk+wk(3)
式中:Xk——k时刻的系统状态;
F——状态转移矩阵;
G——噪声输入矩阵;
Zk——k时刻系统观测输出;
H——观测矩阵;
v(k)——系统噪声;
w(k)——观测噪声。
卡尔曼滤波是利用当前的观测值和上一时刻的估计值更新当前时刻的估计值,其计算过程为:
1)设估计状态初始值为X5。协方差初始值为P5。
2)不考虑系统噪声,根据状态方程进行一步预测,得到状态预测值Xk|k-1:
Xk|k-1=FXk-1(4)
3)根据上一时刻协方差计算下一时刻协方差预测Pk|k-1:
Pk|k-1=FPk-1FT+GQGT(5)
其中Q为系统噪声方差。
4)计算卡尔曼滤波增益Kk:
Kk=Pk|k-1HT(HPk|k-1HT+R)-1(6)其中R为观测噪声方差。
5)结合观测值,计算当前状态的最优估计諼Xk:?
Xk=Xk|k-1+Kk(Zk-HXk|k-1)(7)
6)计算当前时刻的协方差矩阵最优估计值Pk:
Pk=(I-KkH)Pk|k-1(8)
其中:
H=1/T2[1 -2 1](11)
式中:α——状态转移矩阵可调参数,0≤α<1;
T——采样时间间隔。
2.3 基于小波变换的算法优化
列车在行驶时,由于电磁干扰、环境突变等因素影响会导致观测噪声变化。当观测噪声方差改变时,会造成卡尔曼滤波精度下降,甚至导致卡尔曼滤波器发散。小波变换可实现信号和噪声的分离,计算小波变换分离出来的噪声方差,并将其反馈到卡尔曼滤波中更新模型,实现噪声方差的实时估计[11]。
根据Stone-Weierstrass理论,任一有界闭区间的连续函数都可以由该区间内的多项式以任意精度逼近[12]。根据上述定理,加速度信号z(t)可表示为
z(t)=a00+a1t+…+aMtM(12)
其中ai为多项式系数(i=1,2,…,M)。
含噪声的加速度信号Z(t)可表示为
Z(t)=Z(t)+W(t)(13)
根据小波理论内容,ψ(t)为小波函数,其平移变换和尺度变换可表示为
式中:a——伸缩因子;
b——平移因子。
则含噪声的加速度信号Z(t)小波变换可表示为
WZ(a,b)=Z(t)*ψa,b(t)=WZl(a,b)+WZh(a,b)(15)
式中:(*)——卷积算子;
WZl(a,b)——小波系数近似部分;
WZh(a,b)——小波系数细节部分。
根据小波的消失矩理论,若ψ(t)有N个消失矩,且大于M,即N>M,则
由式(16)知,小波变换抑制了信号而保留了噪声分量,则式(15)可表示为
WZ(a,b)=Z(t)*ψa,b(t)=WZh(a,b)(17)
在t时刻噪声的标准差估计值σ为
其中Med(·)为中值函数。
观测噪声方差计算过程如图4所示。为实时计算观测信号噪声方差,可选择一定长度的滑动观测窗口,本文仿真时选取时长为0.5s的滑动窗口。对窗口内的观测信号Z(t)进行小波变换,计算噪声方差并更新卡尔曼滤波的方差数据。
3 仿真分析
3.1 仿真數据获取
为获取验证算法数据,建立高速列车模型。建模时考虑轮轨结构的非线性接触、减振器与横向止档等悬挂结构的非线性特性,车轮采用LMA踏面、钢轨采用60kg标准型钢轨。利用某型高速列车物理参数,建立高速列车多体动力学三维模型,如图5所示。
对列车以350km/b速度进行仿真,轨道谱采用德国五级谱。仿真时间为10s,采样频率为5000Hz。采用轴箱部位的加速度数据和位移数据验证算法。
3.2 算法验证
考虑算法的计算速度,仿真选择消失矩为7阶的db小波进行小波变换,滑动观测窗口长度为0.5s。为验证观测噪声方差对算法的影响,对轴箱加速度数据分别加入不同方差的噪声。第一次加入方差为0.01的噪声,长度为10s;第二次在前5s加入方差为0.01的噪声,从第5s开始噪声方差突变为0.25。
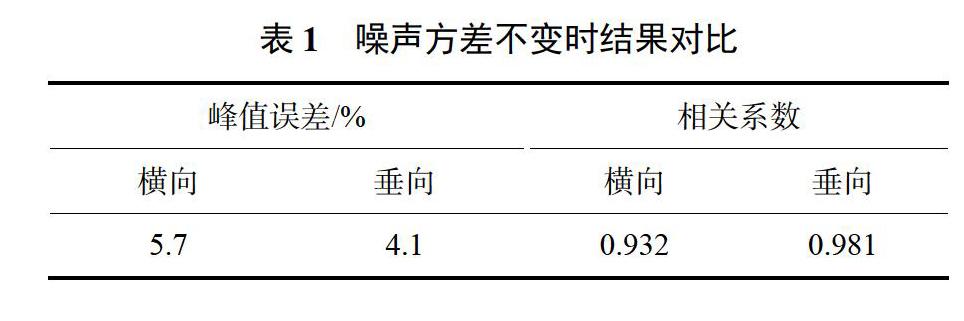
3.2.1 噪声方差不變时计算结果
由图6、7及表1可知,在噪声方差固定时,采用卡尔曼滤波算法可以通过加速度数据对位移进行精确估计。其中横向位移估计值峰值最大误差为5.7%,垂向位移估计值峰值最大误差为4.1%;位移估计结果和仿真位移数据相关系数大于0.9。以上分析说明,在算法中观测噪声方差准确时,卡尔曼滤波算法能精确估计出轴箱横移位移和垂向位移,进而判断列车脱轨状况。
3.2.2 噪声方差改变时计算结果
由图8、9及表2可知,在5s时噪声方差变为0.25,传统卡尔曼滤波由于没有自调整算法中方差数值能力,卡尔曼滤波算法计算结果出现一定程度发散现象,算法精度下降。其中横向位移估计值峰值最大误差为55.6%,垂向位移估计值峰值最大误差为35.2%;横向位移估计结果和仿真位移数据相关系数降低至0.681,垂向位移估计结果和仿真位移数据相关系数降低至0.835。不精确的滤波结果可能导致计算机对脱轨状况的误判。
使用小波变换在线计算观测噪声方差的卡尔曼滤波法,横向位移估计值峰值最大误差降低至5.2%,垂向位移估计值峰值最大误差降低至3.1%;横向位移估计结果和仿真位移数据相关系数提高至0.824;垂向位移估计结果和仿真位移数据相关系数提高至0.927。以上分析说明,使用小波在线计算噪声方差的卡尔曼滤波能够更好地应对观测噪声方差的变化,提高算法抗干扰能力。
4 结束语
本文基于轨道不平顺检测技术,提出一种通过轴箱上安装加速度传感器监测列车脱轨方案,使用卡尔滤波设计脱轨监测关键算法,并通过小波变换对算法进行优化。
1)针对测力轮对维护困难,不适用于高速列车脱轨在线监测的问题,基于轨道不平顺技术的发展,根据轮轨几何关系脱轨理论,从工程可行性角度出发,设计了脱轨在线监测方案。
2)针对测控方案中关键参数轴箱振动位移测量困难、测量误差大的问题,基于卡尔曼滤波设计一种高速列车脱轨检测关键算法,实时计算轴箱振动位移,并引入小波变换在线计算噪声方差对算法进行优化,提高卡尔曼滤波性能。仿真结果表明,在观测噪声方差突变时,算法计算峰值误差为5.2%,具有较高精度。
参考文献
[1]魏来,曾京,邬平波,等.基于轮对模型的铁道车辆脱轨安全性评估[J].铁道学报,2015(9):25-31.
[2]王安吉,张兵,刘晓曼.轮轨垂向力制动台连续测量系统[J].中国测试,2018,44(4):83-87,93.
[3]城取岳夫,王光明.利用转向架振动加速度监视车辆故障的方法研究[J].国外铁道车辆,2014,51(5):36-41.
[4]唐永康.空载货运列车脱轨检测系统的研制[J1.工业控制计算机,2012,25(8):52-53.
[5]钟莎.基于Qt的机车轮轨相对位移的图像检测系统设计[D].石家庄:石家庄铁道大学,2016.
[6]王卫东.高速铁路基础设施综合检测技术[M].北京:铁道科学出版,2017.
[7]熊仕勇.轨道不平顺检测系统中关键技术研究[Dl.成都:西南交通大学,2018.
[8]翟婉明,陈果.根据车轮抬升量评判车辆脱轨的方法与准则[J].铁道学报,2001,23(2):17-26.
[9]杨春雷,翟婉明.车辆动力学仿真中评判脱轨的直接方法[J].交通运输工程学报,2002,2(3):23-26.
[10]卫纬.车辆轨道系统运行安全综合评价研究[D].北京:北京交通大学,2011.
[11]VIMALA C,PRIYA P A.Noise reduction based on doubledensity discrete wavelet transform[C]//InternationalConference on Smart Structures&Systems,2015.
[12]曹忠.基于卡尔曼滤波的电动车窗防夹控制系统研究[D].上海:华东理工大学,2015.
(编辑:商丹丹)
