基于改进经验小波变换的滚动轴承故障特征提取方法研究

刘自然 胡毅伟 石璞 李谦 尚坤

摘要：针对振动信号的非线性、非平稳性和早期故障特征信号难以提取的特点，提出一种基于改进经验小波变换的故障特征提取方法。通过包络分析和对包络曲线进行阈值分割修整的方法来确定经验小波变换分解的模态数和频率边界，解决传统经验小波变换需要预先设置分解模态数和难以对信号频谱进行适当分割问题，以实现对振动信号故障信息更准确的描述。实验表明，该频谱分割方法能够有效检测信号最佳模态分解数，使得信号的频谱分割更为容易、可靠。相比传统EWT和EMD，改进经验小波变换的滚动轴承内圈、外圈Hilbert变换时频图对振动信号的故障相关特征描述更为清晰，在滚动轴承故障特征提取方面表现更为优越。

关键词：滚动轴承;经验小波变换;频谱划分;特征提取

中图分类号：TH113.1 文献标志码：A 文章编号：1674-5124（2019）10-0010-06

收稿日期：2018-12-07;收到修改稿日期：2019-02-20

基金项目：河南省自然科学基金（182300410234）

作者简介：刘自然（1962-），男，河南信阳市人，教授，硕士，研究方向为动态测试技术、机电传动与控制技术。

0 引言

机械设备出现故障往往带来重大经济损失，而其振动信号中含有非常重要的特征信息，通过采集振动信号进行分析处理是一种常用的监测方法。旋转机械出现故障时，振动信号呈现非线性、非平稳性特点，实现该特点下表征故障的敏感特征提取是进行高精度故障诊断的重要前提[1-2]。

EMD是一种自适应时频分析法，能够自适应的提取振动信号不同时间尺度的本征模态函数（intrinsic mode functions，IMF），并通过Hilbert变换求出包络幅值和瞬时频率来表征信号的时频分布[3]。李锋等[4]将EMD与AR模型系数结合验证了该特征提取方法的有效性。Su Zuqiang等[5]通过对EMD分解后的IMFS进行时域、频域等进行特征提取采用LSSVM分类，证明了该方法的有效性。但是EMD存在模态混叠、端点效应以及计算效率低等缺点。为此，Gilles[6]提出一种信号分解方法，即经验小波变换（empirical wavelet transform，EWT），与EMD相比，由于EWT的计算是非递归的，所以它在信号分解方面效率更高。刘自然等[7]通过EWT和包络谱结合验证其在轴承故障诊断的有效性;李志农等[8]将EWT应用于机械故障诊断中，结果表明相比于EMD，EWT消除虚假模态，大大降低计算量。

然而，EWT也存在一些问题，EWT需要预先设置分解的模态数和频率边界，对这些参数的设置不当将导致信号特征的不准确提取，针对此问题，本文提出了一種新的频谱分割方法对传统EWT进行改进，并在滚动轴承上验证了其有效性。

1 经验小波变换简介

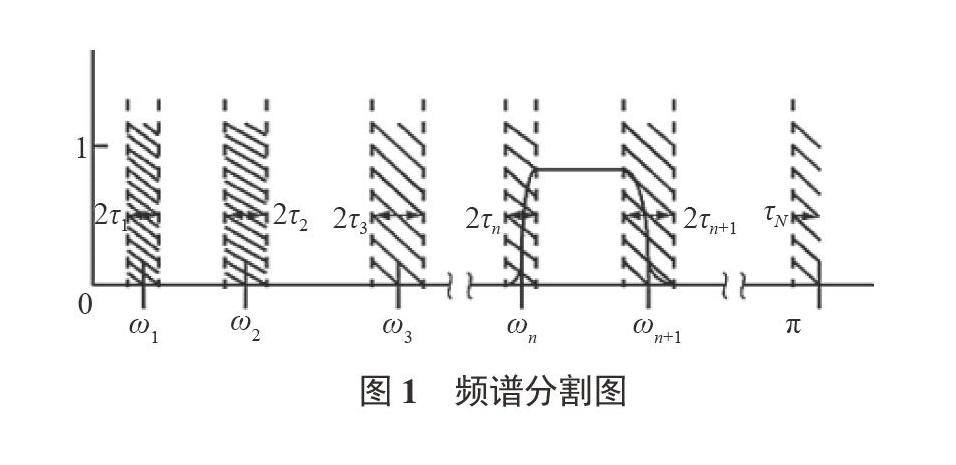
EWT首先用N+1条边界线将傅里叶频谱划分成N个连续的区间，除去0和π两个边界，还需要N-1个边界，每个分割的区间表示为∧_n=[ω_n-1，ω_n]，n=1，2，…，N（ω₀=0，ω_N=π）。其中围绕每个ω_n都定义一个过渡段T_n（宽度是2τ_n），τ_n=τω_n，γ为系数[9-10]。具体划分如图1所示。

确定分割区间∧_n后，根据Meyer小波的构造方法构建经验小波，经验尺度函数和经验小波函数[11]分别为：

|ω|≤ω_n-τ_n

信号重构的结果如下：

通过上式可知经验模态函数f_k，公式如下：

可以看出：EWT具有从非线性、非平稳性信号中提取AM-FM分量的优点，然而其还具有一定的局限性如下：

1）EWT需要预先设置分解的模态数，而设置了不恰当的分解模态数将会影响特征提取效果。

2）上文中通过τ_n=γω_n构造的不同中心频率的滤波器是一种平均划分的带宽定义方法，对于变工况下特征频率变化的振动信号不能自动定义带宽区间。

2 改进经验小波变换

本文提出的频谱分割方法先对信号的频谱进行包络分析，再通过阈值分割对所得包络曲线进行修整。在修整后包络曲线中，能够明显识别出信号的主频率分量，主频率分量将用于确定EWT的模态数和频率边界。假设振动信号x（t），改进EWT频谱分割方法步骤如下：

1）对x（t）进行FFT，即：

F（s）=FFT（x）（8）

A_ax=|F（s_i）|（i=1，2…，l）（9）其中，l为信号x（t）内所包含的一半的数据。

2）查找A_ax的局部极值。

3）用三次样条插值法生成傅里叶谱包络曲线。

4）计算阈值T：

T=Al+r（A_h-A_l）（10）

r=C/SNR（11）其中，A_h、A_l分别为频谱中的最大值和最小值。r与信噪比（SNR）成反比。常数C控制阈值的大小。本文假设振动信号的信噪比大于85dB，C=10，则r取0.1。

5）使用计算的阈值修整包络曲线，并检测修剪后的包络曲线中的所有极值。

6）定位所有局部极大值点。局部极大值点的个数即为EWT分解的模态数，其频率用于定义模态的中心频率。

7）定位所有局部极小值点并按升序排序，即ω=ω₁，…，ω_n-1，ω_n，…，ω_N，用来进行频谱分割。

通过上述频谱分割改进方法可得知，第五步的修整过程能够确定不同振动信号所分解的模态数量;并且在包络曲线中采用局部附加的方法定义模态边界，可使频谱分割过程更为简便。

3 改进经验小波变换分析

通过一组正常状态轴承信号验证所提频谱分割方法的有效性，其时域图见图20对信号进行FFT，得到的频谱图和包络曲线如图3所示。

利用式（10）进行阈值计算，得T=2。再通过阈值对包络曲线进行修剪，得包络曲线如图4所示。

通过所提方法的6）和7），利用修剪得到的包络曲线来分割频谱。图4中模態的频率边界由虚线表示。不难看出，该信号的频谱共被分割成11个部分，由6个主模态边界组成。

为检验所提频谱分割方法的效果，对原始信号和EWT分解重构的信号进行相关分析。假设EWT分解的模态数越多，其重构信号与原始信号的相关性越大。为得到两者相关性的变化趋势，本文预先设置EWT分解模态数为11，并利用EWT对图2信号进行分解再重构，重构信号与原始信号相关系数的公式如下：其中，x为原始信号，表示重构信号，其中n从1增加到11，表示用于信号重构的模态数。

相关系数值C（n）与信号重构模态数的变化趋势如图5所示。

从图中可知，随着n的增加，C（n）也逐渐变大，当n为11时，C（n）趋近于1。同时可观察到当n=1，2，4，6，8和10时，C（n）出现明显的增长。代表这6种模态为信号主要特征，即这6种模态重构的信号能够有效刻画原始信号的主要特征。此结果与所提分割方法的结果相一致。表明本文所提频谱分割方法能够有效检测信号最佳模态分解数。

本文所提改进EWT流程图如图6所示。

4 改进经验小波变换实验验证

本实验利用已开放供研究的凯斯西储大学轴承数据中心轴承故障数据进行验证。通过电火花加工（EDM）对电机轴承内圈和外圈设置直径约0.2mm的故障损伤。实验台由电机速度控制器，2马力电机，模拟载荷等组成。当电机转速为1750r/min时通过加速度传感器采集内圈故障和外圈故障的振动信号，采样频率为12kHz。两种信号的时域波形图如图7所示。

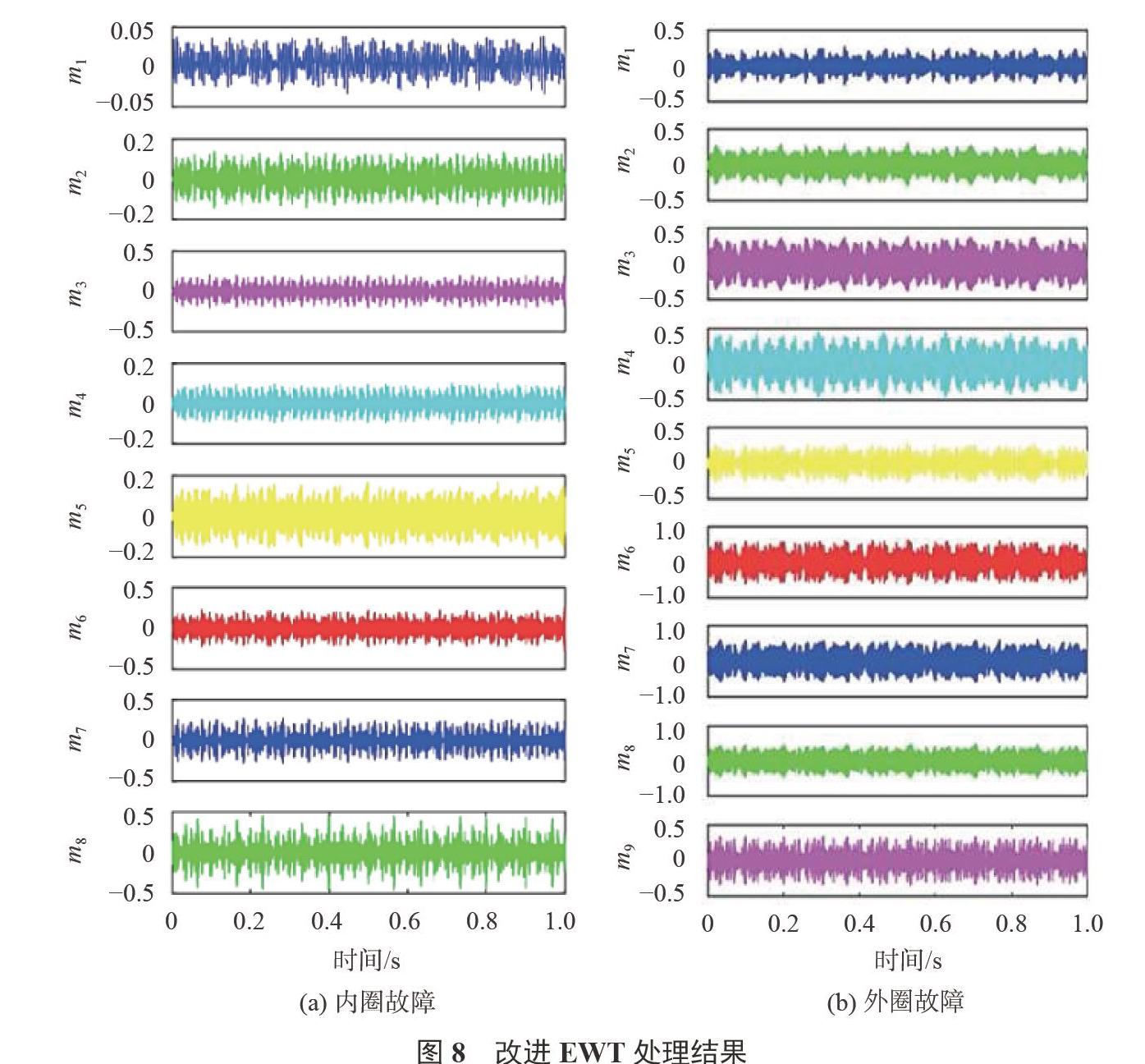
从图中可以看出，两种振动信号都存在很强的背景噪声，可以明显看出振动信号中包含复杂的冲击特征。通过改进EWT对两种振动信号处理得到的主要模态如图8所示。

为了准确描述故障相关的特征，通过对图8所示的各个模态函数进行Hilbert变换，图9为相应的两种故障信号的时频图。受计算机内存的限制，在时频分析中只处理图8（a）、8（b）中的前0.1s数据。同时为了对比改进EWT效果，图9展示了使用传统的EWT得到的时频图。

对图9所示结果进行比较可知：

信号中包含的与故障相关的周期性冲击特征已被改进EWT显式地检测出来。从这些周期性冲击特征之间的时间间隔可以很容易地估计出故障的特征频率，因此，在已知轴承的规格参数情况下，能够准确地诊断故障类型。相反，传统小波变换导出的时频图中冲击特征表现不明显，甚至被背景噪声掩盖，导致它们之间的时间间隔很难估计，这将增加信号解析的难度。

传统EWT结果中存在大量改进EWT结果所不存在的干扰分量。说明改进EWT能够将振动信号的主频率分量准确提取出来的同时对信号中存在的干扰和噪声的抑制效果更好，从而使信号的时频图更加整洁、易于观察。

在此基础上，对改进EWT和DM进行对比，以说明改进EWT对非线性和非平稳振动信号特征提取的优越性。图7中两个信号的对应OM结果如图10所示。

从图10中可以看出，在早期故障阶段信号中的冲击特征很弱的情况下，能够被改进EWT准确提取出的故障冲击特征通过EMD方法不能实现成功提取。

实验表明，与EMD和传统EWT相比，改进EWT在准确提取非线性非平稳性状态监测信号的时频特征方面的效果更好。因此通过改进EWT得到的精确、整洁的时频特征对于滚动轴承故障诊断具有更大的帮助。

5 结束语

EWT在信号分解和特征提取方面均优于EM1）。然而，EWT结果的准确性在很大程度上取决于模态数的正确设置和每个模态的频率边界划分。为解决此问题，本文提出了一种改进的EWT方法，并进行了实验验证，得到结论如下：

1）传统的EWT方法由于缺乏对所研究信号的频谱进行适当分割的方法，因此无法对信号的频谱进行适当分割。而信号频潜分割不当将会降低EWT的计算效率以及降低特征提取的准确性。

2）利用所提出的频谱分割方法，可以很容易地确定每个EWT模态的模态数目和频率边界。此外，通过改进EWT得到的每个EWT模态都具有滚动轴承特征相对应的确切物理意义。而传统EWT将未识别的信息包含在结果中，将会增加信号解析的难度，甚至误导滚动轴承的状态监测。

3）实验表明，尽管信号中含有相当大的噪声，改进EWT仍能更精确地提取与故障相关的信号时频特征。与传统EWT相比，改进EWT需要较少的人为参与，因此有可能成为一种完全由数据驱动的信号处理技术。

参考文献

[1]吴印华，徐琼燕，李俊峰.基于局部特征尺度分解排列熵和线性局部且空间排列的故障特征提取方法[J].机械设计与研究，2017，33（1）：27-30，34.

[2]张良，张前图.基于LCD模糊熵和流行学习的故障特征提取方法[J].机械强度，2016，38（2）：225-230.

[3]宋金波，王德平，刘霞.基于EMD瞬时功率谱熵的神经网络滚动轴承故障诊断[J].化工自动化及表，2016，43（8）：793-796.

[4]李锋，汤宝平，陈法法.基于线性局部切空间排列维数化简的故障诊断[J].振动与冲击，2012，31（13）：36-40，61·

[5]SU Z Q，TANG B P，LIU Z R，et al.Multi-fault diagnosis forrotating machinery based on orthogonal supervised linear localtangent space alignment and least square supportvectormachine[J].Neuro-Computing，2015，157（1）：208-222.

[6]GILLES J.Empirical wavelet transform D].日;EE Transactionson Signals Processing，2013，61（16）：3999-4010.

[7]刘自然，陈仁权，颜丙生，等.基于EWT和包络谱分析的轴承故障诊断研究[J].中国测试，2018，44（2）：98-102.

[8]李志农，朱明，褚福磊，等.基于经验小波变换的机械故障诊断方法研究[J].仪器仪表学报，2014，35（11）：2423-2432.

[9]向玲，李媛媛.经验小波变换在旋转机械故障诊断中的应用[J].动力工程学报，2015，35（12）：975-981.

[10]祝文颖，冯志鹏.基于改进经验小波变换的行星齿轮箱故障诊断[J].仪器仪表学报，2016，37（10）：2193-2201.

[11]FRANCIS A，MURUGANANTHAM C.An adaptive denoisingmethod using empirical wavelet transform[J].InternationalJournal of Computer Applications，2015，117（21）：18-20.

（编辑：刘杨）