基于DIHPB 技术的高应变率剪切测试方法*

刘 宇，许泽建，汤忠斌，张炜琪，黄风雷

（1. 北京理工大学爆炸科学与技术国家重点实验室，北京 100081；2. 西北工业大学航空学院，陕西 西安 710072）

金属材料在受到爆炸、冲击、侵彻及高速切削等高应变率载荷时，往往处于剪切主导的应力状态，并进而引发失效。在上述过程中，材料的剪应变率有时可以达到105s-1。因此，对金属材料在高应变率下剪切力学性能及失效机理的研究，具有重要的科学意义及工程价值[1-3]。

为研究材料的动态剪切性能，Baker 等[4]首次提出了Hopkinson 扭杆装置。采用该方法，可以获得材料在动态加载下的剪应力-剪应变曲线，剪应变率一般在103s-1量级[5-7]。此外，还可以采用分离式霍布金森压杆（SHPB）技术对不同形状的试样进行加载，使其局部发生剪切变形，从而获得材料的动态剪切性能。例如，Hartmann 等[8]提出的帽型试样被广泛用于材料绝热剪切带的测试研究[9-11]。但是，采用该试样很难获得均匀变形场和纯剪切的应力状态，因此难以准确测得材料的剪应力-剪应变曲线[12]。Rusinek 等[13]利用改进的SHPB 实验装置对双剪切试样进行了动态剪切测试，但是需要通过数值模拟对所测的参数进行修正。Rittle 等[14]利用预制刻槽的圆柱试样，对材料在压缩-剪切状态下的动态性能进行测试。Guo 等[15]采用改进的微型压杆装置，对双剪切试样进行加载，获得材料的剪切性能。近年，许泽建等[16-17]提出了一种新型双剪切试样，可以在传统SHPB 装置下获得104s-1以上的剪应变率，对材料在剪切载荷下的塑性流动及失效行为[18-19]进行研究。

直撞式霍布金森压杆（DIHPB）技术在传统的SHPB 中，去掉入射杆而使子弹直接撞击试样，从而避免入射杆弹性对子弹速度的限制以获得更高的应变率。例如：Gorham[20]利用DIHPB 系统，测量了铜在105s-1应变率下的压缩应力-应变曲线；Dharan 等[21]和Zhao[22]分别采用该方法对铝和混凝土类材料的压缩特性进行了研究；陶俊林等[23-24]对DIHPB 方法进行了数值模拟及理论分析。本文中，基于近期提出的新型双剪切试样，采用DIHPB 技术对603 钢进行高应变率下的动态剪切测试，并与SHPB 实验结果进行对比。采用数值模拟验证该方法的准确性，并对该方法的适用条件进行分析。

1 实验方法

实验材料为603 装甲钢，所采用的双剪切试样及配套夹具见图1。双剪切试样具有一个加载端和两个支撑端，他们之间是两个对称的剪切区，本文中使用的剪切区宽度为0.5 mm。

实验所用DIHPB 系统包括子弹、透射杆和能量吸收装置。子弹长度为50 和20 mm，透射杆长度为500 mm，子弹和透射杆直径均为19 mm；子弹材料为18Ni 钢，透射杆材料为7075 铝合金，透射杆上的应变信号由应变片测得。实验中，采用激光测速装置对子弹初速度进行测量。先通过标尺对电压和位移的对应关系进行标定，再根据子弹经过时的电压曲线计算子弹的初速度。由测试结果可知，子弹在接触试样前后的速度变化较小，因此可近似认为子弹在撞击过程的速度为恒定值。该方法的实验原理如图2 所示。

图1 新型双剪切试样及夹持装置示意图Fig. 1 Illustration of NDSS sample and fixture

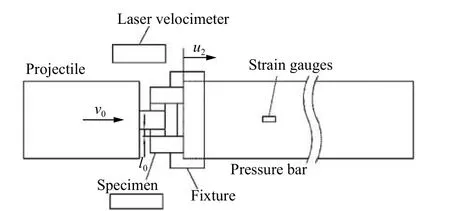
图2 DIHPB 系统实验原理图Fig. 2 Illustration of experimental system

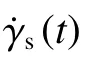
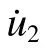
根据一维应力波理论，有：

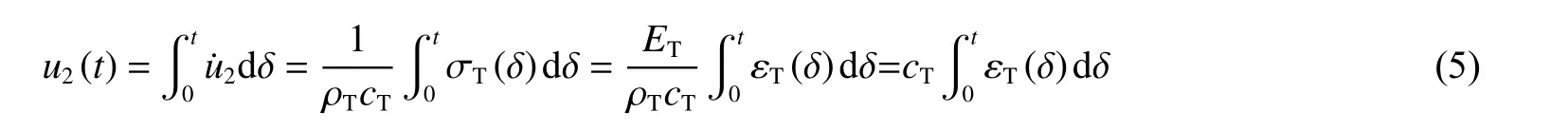
式中： ρT、cT分别为透射杆的密度和弹性波速。

由式（1）～（5）可知，试样的剪应变率、剪应变和剪应力分别为：

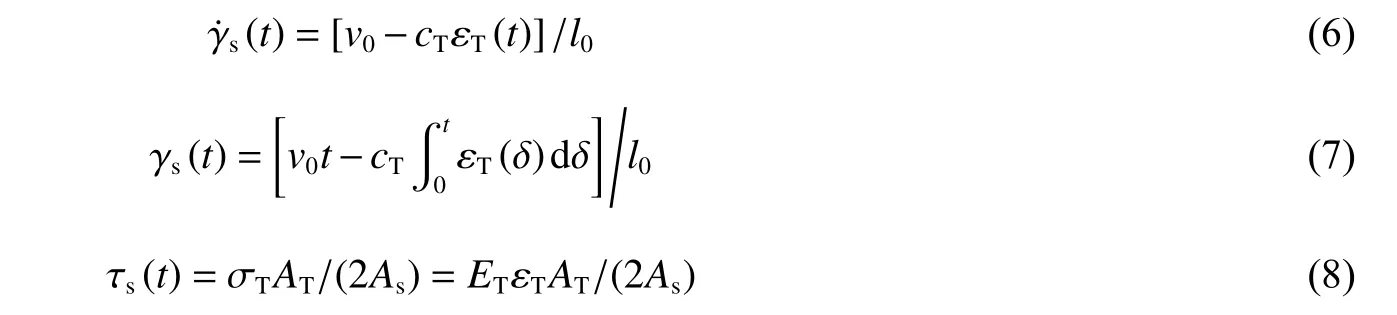
因此，根据式（6）～（8），可由实验测得的透射应变信号和子弹初速度，得到试样的剪应力-剪应变曲线。

由于603 钢屈服应力约为800 MPa，密度ρs为7.8 g/cm3，弹性波速cs为5 189 m/s。根据假设，由σ=ρscsvc，可知603 钢试样加载端发生屈服的临界子弹速度vc约为19.77 m/s。当撞击速度超过该值时，试样的加载端会发生塑性变形，此时由式（7）计算得到的剪应变会存在一定误差。因此，采用上述方法测试材料的剪应力-剪应变曲线时，子弹速度不应高于临界速度vc。

2 实验结果

分别在不同子弹速度下进行了冲击剪切测试，实验前后的典型试样形貌见图3。图中对比了未加载及在9.52 和72.79 m/s 速度下加载后的试样。在两种加载速度下试样剪切区均发生断裂；在9.52 m/s 加载速度下，试样加载端未发生塑性变形，但在72.79 m/s 速度下试样的加载端发生了明显的塑性变形。图4 为在4 种加载速度下由透射杆上的应变片测得的应变曲线。只有1.96 m/s 速度下试样未发断裂，因此该速度下得到的透射应变脉宽明显大于其他曲线。此外，随着子弹速度的增加透射应变的脉宽逐渐减少，这说明随着加载速度的增大，试样发生断裂的时间逐渐缩短。在以上速度下获得的603 钢剪应力-剪应变曲线见图5。

图3 603 钢实验前后的试样Fig. 3 Specimens of 603 steel before and after experiment

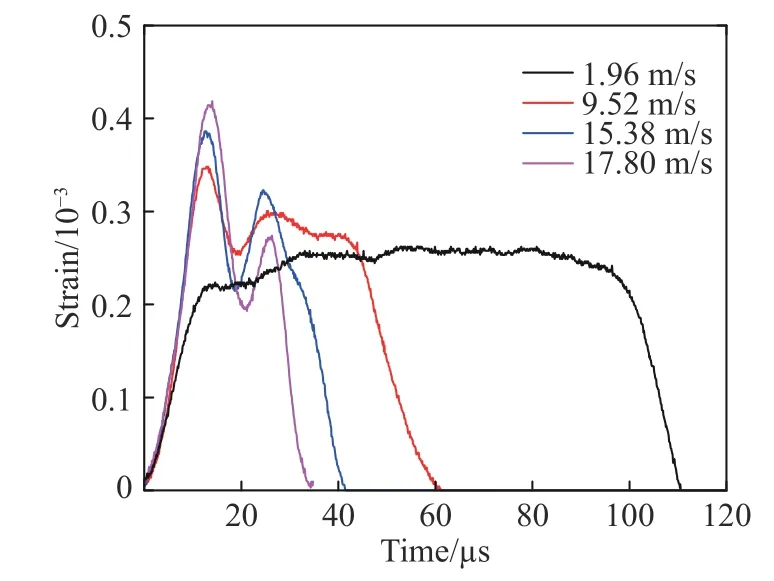
图4 不同加载速度下的透射应变曲线Fig. 4 Transmission strain curves of 603 steel at different projectile velocities

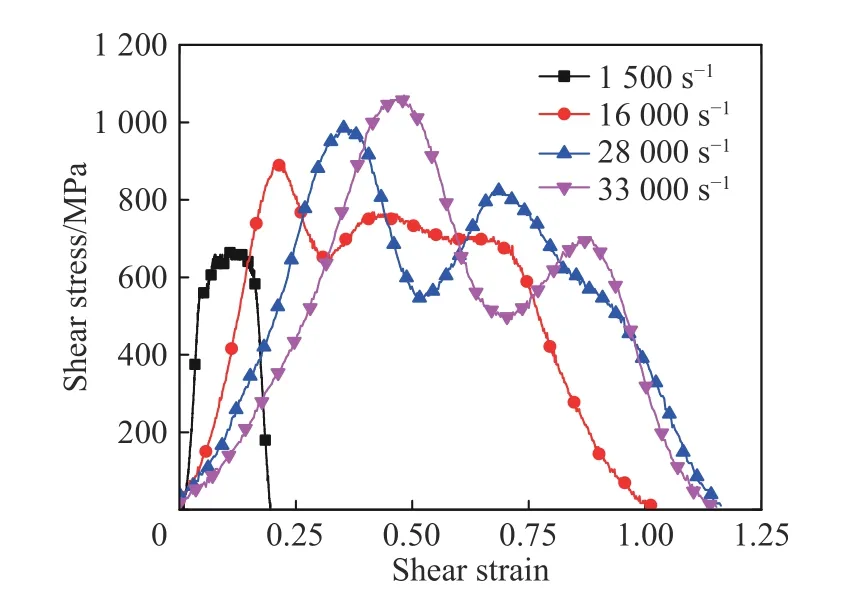
图5 不同应变率下的剪应力-剪应变曲线Fig. 5 Shear stress-shear strain curves of 603 steel at different strain rates

由图5 可知，603 钢的流动应力存在明显的应变率效应。随着应变率的增加，实验曲线幅值逐渐升高。当应变率为1 500 s-1时，剪应力-剪应变曲线的流动应力段较短,稳定段幅值约为642 MPa。当应变率为16 000 s-1时，曲线初始段出现明显的尖峰，但此后的流动段较稳定，幅值约为730 MPa。曲线初始段的峰值可能是由压杆端部的横向惯性效应而引起的波形弥散，该现象随着应变率的增加而趋于明显。当应变率超过28 000 s-1时，曲线没有明显的流动段而只有两个峰值，且第2 个峰值明显较低。结合实验观测可知，第2 个波峰由试样的失效造成，即材料在该处发生剪切破坏，因此剪应力此后呈现迅速下降趋势。此外，随着加载速度的提高，曲线上升沿的斜率逐渐减小。这是由于，在较高的加载速度下材料在初始阶段的变形速度也相应较高，因此材料的剪应力在到达第1 个峰值时的应变值也相对较大。

为了验证DIHPB 系统的准确性，使用相同的双剪切试样在SHPB 系统下测得近似应变率下的剪应力-剪应变曲线，并与DIHPB 结果进行对比，如图6 所示。在应变率接近16 000 s-1时，由SHPB 和DIHPB 系统测得的剪应力-剪应变曲线在流动段吻合较好，但SHPB 曲线的上升沿斜率大于DIHPB 曲线。在剪应变率接近30 000 s-1时，两条曲线均存在两个波峰，而且峰值较接近，但DIHPB 曲线的峰值明显偏后于SHPB 曲线。为分析该现象，将不同测试系统下获得的应变率曲线进行对比（见图7）。可以看出，DIHPB 方法在加载过程中剪应变率先由大变小并趋于稳定，而SHPB 方法中剪应变率由零上升至峰值并趋于稳定，即初始阶段DIHPB 方法获得的剪应变较大，这就导致DIHPB 曲线上升沿斜率明显小于SHPB 曲线。但是由图7 可知，由SHPB 和DIHPB 方法获得的应变率曲线均能达到稳定阶段，说明两种方法下均能获得较恒定的剪应变率。另外，当只考虑材料的塑性流动阶段时，两种方法所测得的结果具有较好的一致性。

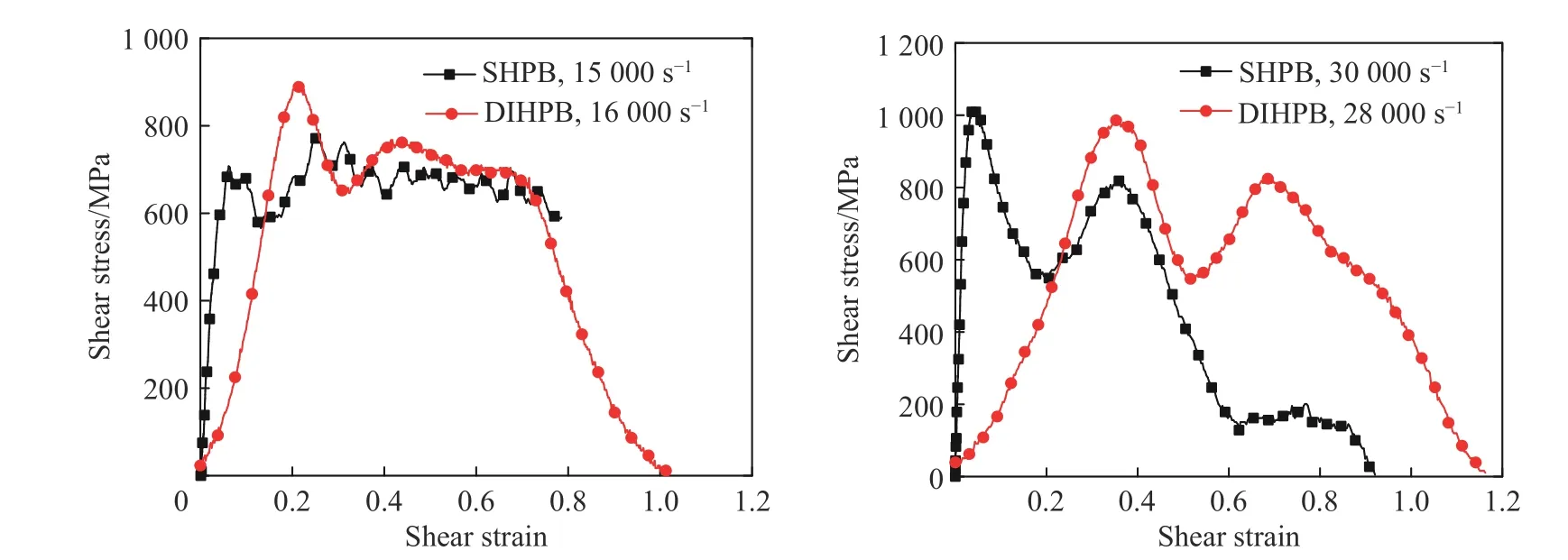
图6 DIHPB 及SHPB 方法在相似应变率下的实验结果对比Fig. 6 Comparison of shear stress-shear strain curves between DIHPB and SHPB systems at close strain rates

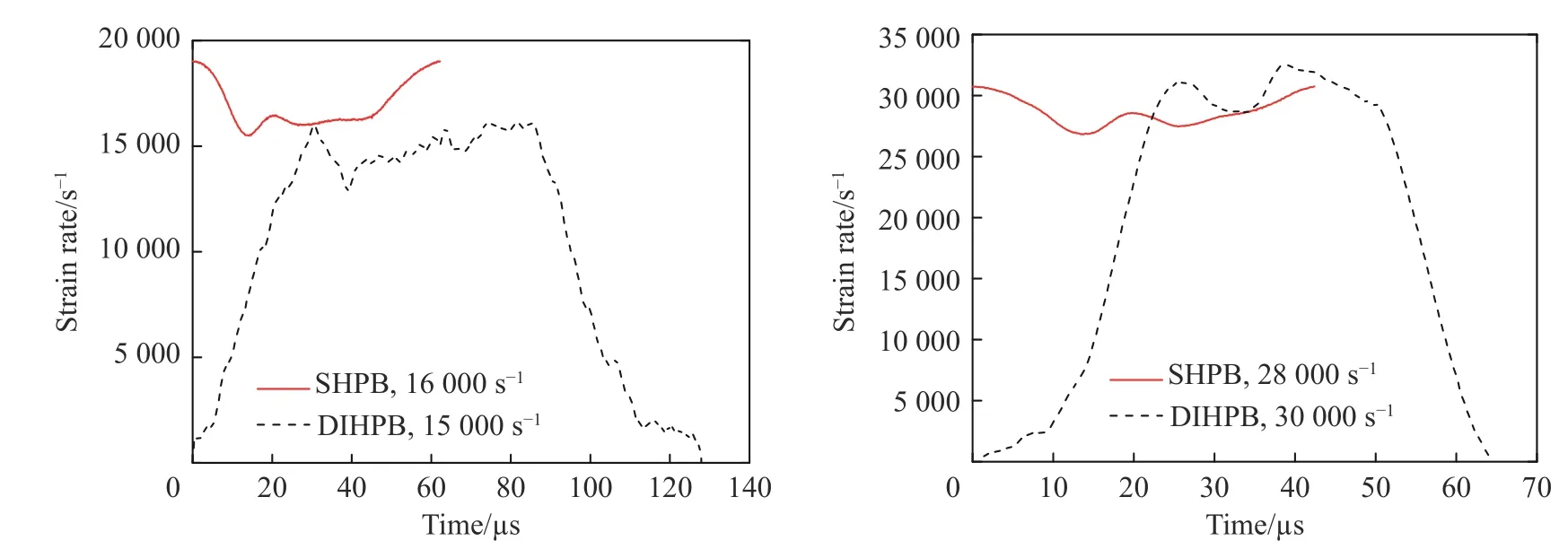
图7 DIHPB 及SHPB 方法的应变率曲线对比Fig. 7 Comparison of shear strain rate curves between DIHPB and SHPB systems

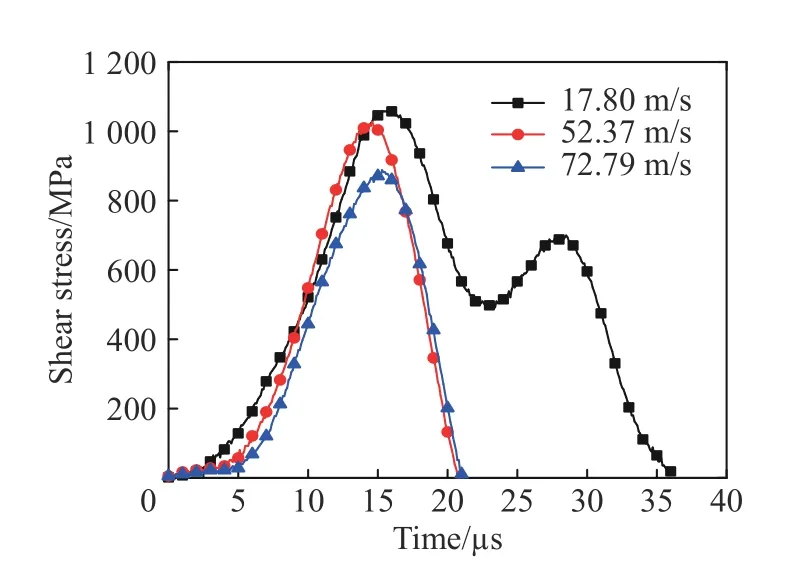
图8 603 钢高速加载下的剪应力曲线Fig. 8 Shear stress curves of 603 steel at higher projectile velocities

在更高的加载速度下获得的剪应力曲线与17.80 m/s 下的曲线对比，如图8 所示。在17.80 m/s 加载速度下，剪应力曲线仍然存在两个峰值；当加载速度分别提高到52.37 和72.79 m/s时，试样加载端已出现塑性变形，可观察到两条曲线均只有1 个峰值。这是由于，在较高的撞击速度下，材料在加载波的上升沿即发生失效。而且由于，随着应变率的增加材料内的绝热温升现象更加明显，导致剪应力峰值随着加载速度的增加而逐渐减小。同时可知，在较高的加载速度下，由于试样迅速失效（＜20 μs），因此加载过程并未达到恒定的应变率；另外，此时试样内部的应力分布尚未均匀，试样两端难以达到受力平衡，因此由式（8）得到的剪应力也存在误差。由以上分析可知，在采用DIHPB 方法对该双剪切试样进行加载时，当加载速度超过临界速度以后，很难获得准确的材料参数，必须借助数值模拟对受力情况进行具体分析。

3 数值模拟

为进一步验证实验结果的准确性，采用有限元软件ABAQUS/Explicit 对DIHPB 实验过程进行了数值模拟。模拟采用三维实体模型，包括子弹、试样、夹具及透射杆，模型的几何尺寸、位置关系及接触情况与实际情况一致。通过对子弹施加实测的预定义速度对试样进行加载，各接触面的接触关系均为“硬”接触。子弹、夹具和透射杆均采用C3DR8 六面体缩减积分单元；考虑到试样发生剪切变形时存在明显的局部温升，因此试样采用C3D10MT 四面体位移温度耦合单元，同时对试样剪切区的网格进行加密处理，见图9。试样的预定义温度场为298 K。

图9 有限元模型及网格划分情况Fig. 9 Finite element model and meshing

由于撞击杆不发生塑性变形，因此定义为弹性材料；试样和透射杆则采用Johnson-Cook 热黏塑性本构模型，本构关系如下：

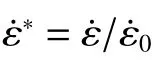
表1 模拟中的材料本构Table 1 Material constants for Johnson-Cook model

表2 模拟中的材料物理参数Table 2 Material parameters used in finite element simulation

为了验证在实验过程中试样两端面的受力平衡，在模拟结果中输出撞击杆与透射杆端面的受力曲线，如图10 所示。可以看出，在不同加载速度条件下，试样两端受力过程接近平衡。在17.80 m/s 时，加载的初始阶段由于试样中的应力波尚未达到均匀传播，因此导致两端的受力存在一定差别，随着应力波多次反射试样两端的受力逐渐趋于平衡。

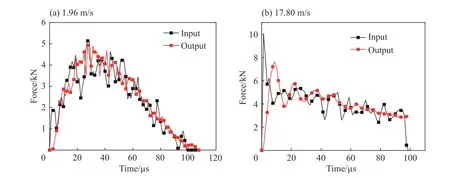
图10 模拟中撞击杆及透射杆端面的受力曲线Fig. 10 Force curves at projectile and transmitter bar ends in simulation

透射杆中应变信号的模拟与实验结果对比见图11，模拟与实验曲线的幅值吻合较好。两条曲线都具有两个明显的峰值，实验曲线在第2 个峰值以后迅速降为零，这是由于试样在实验过程发生断裂而导致的；由于在模拟中并未考虑材料的失效，因此模拟曲线未出现迅速下降。将实验测得的剪应力、剪应变转化为等效应力和等效应变：

并比较实验和模拟得到的剪应力-剪应变曲线和等效应力-等效应变曲线，如图12 所示。由于实验结果是由透射杆上测得的应变信号得到的，因此实验曲线存在由应力波的传播而引发的波动；而模拟曲线是由试样剪切区所有单元计算结果的平均值获得的，因而表现出较平滑的特征。但是，由模拟得到的剪应力-剪应变曲线和等效应力-等效应变曲线的幅值均与实验结果吻合较好，说明DIHPB 系统测得的动态剪应力-剪应变曲线具有较好的准确性。

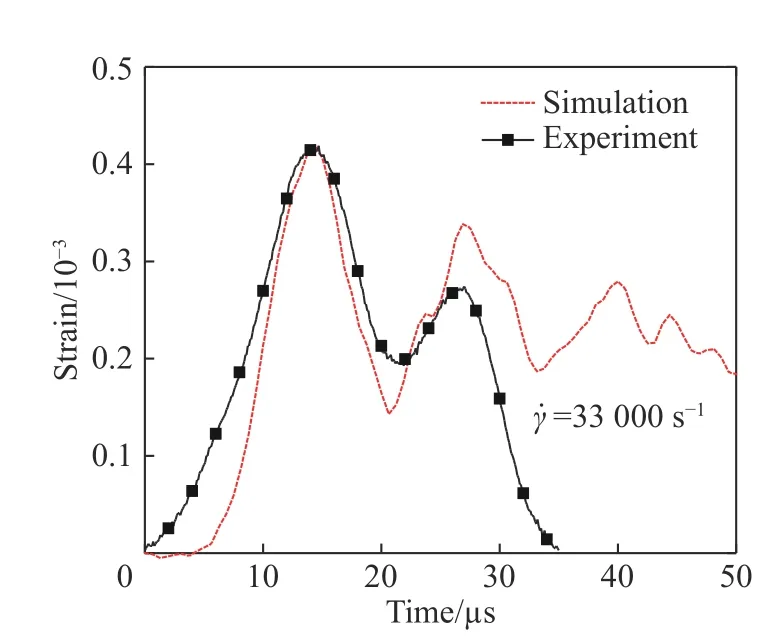
图11 透射杆应变曲线的模拟与实验结果对比Fig. 11 Comparison of transmission strain curves between experimental and simulation results

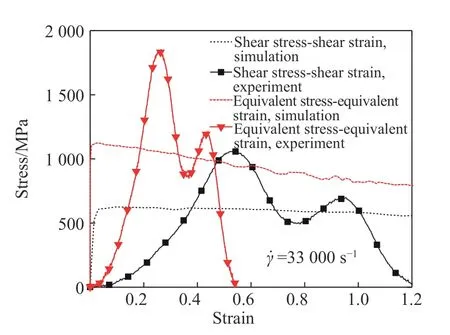
图12 应力-应变曲线的模拟与实验结果对比Fig. 12 Comparison of stress-strain curves between experimental and simulation results

当子弹速度超过临界加载速度时，由于试样加载端将发生塑性变形，因此试样的实际响应必须通过数值模拟获得。例如，当子弹速度为72 m/s 时，对实测结果和模拟得到的透射杆应变信号的第1 个波峰进行对比，如图13 所示。由图13 可知：两曲线在前期吻合较好，且出现峰值的时刻较一致；但在约11 μs 时两曲线发生分离，且模拟结果大于实测结果。这可能是由于，在实际加载下材料在高速剪切过程中产生了绝热剪切带或微裂纹等形式的损伤，但模拟中并未考虑材料的损伤及失效，从而引起实验曲线低于模拟结果。

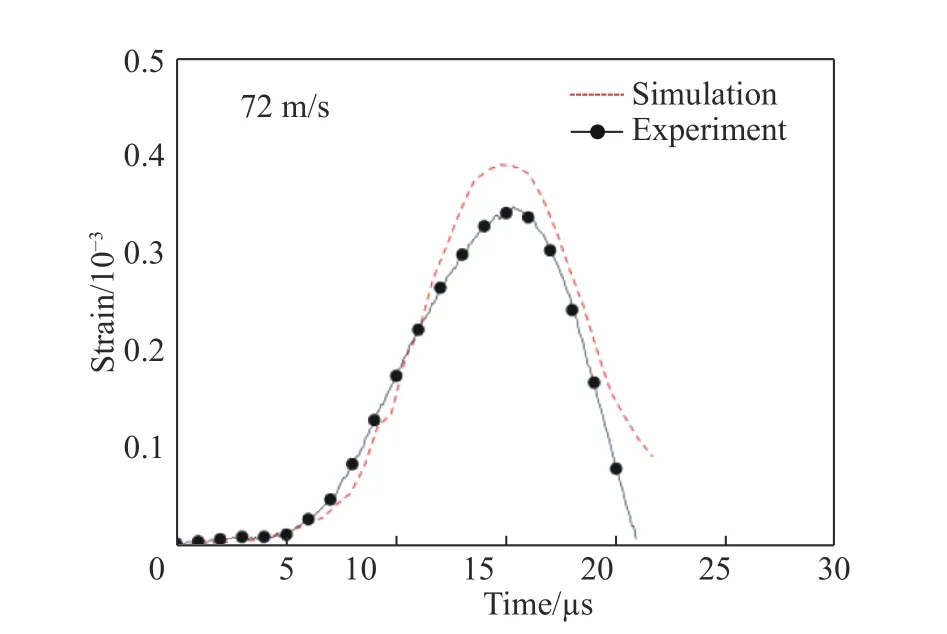
图13 透射杆应变的模拟与实验结果对比Fig. 13 Comparison of transmitted strain curves between experimental and simulation results

4 结 论

采用DIHPB 加载技术对新型双剪切试样进行了冲击加载，获得了603 钢在高应变率下的动态剪切特性。通过与SHPB 测试结果及有限元模拟结果的对比分析，验证了该方法的有效性。主要结论如下。

（1）基于DIHPB 系统测试方法，使用近年来提出的新型双剪切试样得到了603 钢在剪应变率1 500～33 000 s-1之间的剪应力-剪应变曲线。通过SHPB 对比试验，发现两种方法下均能获得较恒定的剪应变率，但流动应力曲线的上升沿存在差别。当只考虑材料的塑性流动阶段时，两种方法所测得的结果具有较好的一致性。

（2）采用ABAQUS/Explicit 对DIHPB 方法的加载过程进行了模拟。通过与实验结果进行对比，发现两者的透射应变信号及应力-应变曲线均吻合较好，且试样两端满足载荷平衡条件，进一步验证了DIHPB 加载方法的可靠性。

（3）采用DIHPB 方法可以观察到：603 钢的流动应力存在明显的应变率强化效应，即随着应变率的增加而逐渐增加；但在较高的加载速度下，材料的失效应力随着加载速度的增加而出现降低趋势。

（4）使用DIHPB 系统对新型双剪切试样进行加载时应注意：子弹速度应低于临界速度，否则由式（7）得到的剪应变会存在一定误差；当子弹速度超过临界速度，试样两端的受力情况也趋于复杂，可能引起试样的受力平衡条件不再满足，因此由式（8）得到的剪应力也存在误差。