使用新型物态方程的超高速碰撞物质点法模拟*

李依潇，王生捷

（1. 中国航天科工集团第二研究院研究生院，北京 100854；2. 北京机械设备研究所，北京 100854）

超高速碰撞是指“材料强度远小于自身所受惯性力”[1]的碰撞。超高速碰撞现象广泛存在于航天、兵器、天体物理等领域。超高速碰撞问题具有复杂性，涉及固体力学、流体力学、热力学等多门学科，理论研究存在较大困难，实验研究受到成本、技术等方面的限制，因此数值模拟成为研究超高速碰撞问题的重要手段。

物质在超高速碰撞过程中大变形、高应变率、破碎等表现，给数值模拟带来巨大挑战。数值模拟的核心是数值计算方法，即对连续介质的离散近似。拉格朗日法将计算网格固连在物体上，在求解超高速碰撞问题时会发生网格畸变，无法有效模拟材料破碎等现象；欧拉法将计算网格固定在空间中，材料相对网格运动，不存在网格畸变问题，但控制方程存在对流项，求解较困难；针对以上两种方法的优缺点，任意拉格朗日-欧拉法(arbitrary Lagrange-Euler, ALE)将两者结合使用，可解决一大批只用拉格朗日法或欧拉法解决不了的问题。为克服网格法存在的不足，无网格法应运而生。光滑粒子流体动力学(smoothed particle hydrodynamics, SPH)方法将计算域离散为一系列有相互作用的粒子，这些粒子承载质量、速度、能量等物理量，通过核函数发生相互作用。SPH 方法在超高速碰撞问题数值模拟中得到广泛应用，但仍存在固有的缺陷，如计算效率低、拉伸不稳定、边界条件难以处理等。物质点法(material point method, MPM)是一种采用拉格朗日质点和欧拉网格双重描述的数值计算方法，综合了网格法和无网格法的优点，非常适合分析超高速碰撞问题。物质点法的基本思想是将连续体离散成一组带有质量的质点，并在物质运动区域建立背景网格，质点携带质量、速度、应力、应变、能量等物质信息，网格仅用于动量方程的求解与空间导数的计算，在每一个时间步中，质点与网格完全固连，在时间步结束时丢弃已变形的背景网格[2-3]。

在超高速碰撞问题中，材料的强度与其所受的压力相比可以忽略不计，材料处于流动状态，材料中的压力需要使用物态方程来计算。物态方程用于描述物质压力、内能、体积的函数关系，在物质点法模拟的每一时间步内，通过将所求得的质点体积、内能代入物态方程，解得当前时刻质点的压力。Mie-Grüneisen 物态方程形式简单，可以很好地描述绝大多数金属固体在冲击载荷作用下的热力学行为，常用于冲击动力学问题的数值模拟[2,4]。Tillotson 物态方程考虑材料的凝聚态和气态，没有考虑熔化，主要优点是适合于高压区域[5]，在冲击动力学问题数值模拟中的应用也很广泛，碰撞速度高于4 km/s 的问题就应该使用Tillotson 物态方程计算[6]。由于超高速碰撞问题涉及材料液化、汽化等相变现象，在数值模拟中使用Mie-Grüneisen 物态方程或Tillotson 物态方程，会导致计算结果与实验结果存在偏差。本文中结合Grover 定标律方程与分子动力学方法，计算得到金属铝的新型物态方程，并代入MATLAB 自编柱坐标物质点法计算程序，将计算所得碎片云与实验结果，使用Mie-Grüneisen 物态方程、Tillotson 物态方程的计算结果进行对比，证明新型物态方程的有效性。

1 物质点法基本原理

1.1 控制方程

在超高速碰撞问题中，碰撞点附近区域的压力远高于材料本身强度，可以认为该区域的材料是可压缩流体。材料在超高速碰撞过程中经历高应变率的变形，变形过程很短暂，可忽略热传导效应[7]。轴对称冲击动力学分析常使用柱坐标形式的更新拉格朗日格式控制方程[8-9]。

质量守恒：

动量方程：

能量方程：

控制方程是一组偏微分方程，求解此类方程的方法分两类：一类是直接求解；另一类是先建立和原微分方程及其定解条件等价的弱形式，再以此为基础建立近似解法[2]。物质点法的求解采用后一种方法。

1.2 离散形式

物质点法将连续体离散为一系列质点，质点的运动代表了物体的运动。物质点法采用质点积分，即将虚功方程中的各项积分转化为被积函数在各质点处的值与该质点所代表的体积乘积的和。在求解动量方程时，质点和背景网格完全固连，随背景网格一起运动，质点和网格结点之间通过形函数NIp建立信息的映射。质点携带的位移、应力等信息的导数，可以由结点信息插值得到。质点与结点之间的信息映射公式[2]如下。

质点坐标：

质点位移：

质点位移导数：

结点质量：

结点动量：

结点内力：

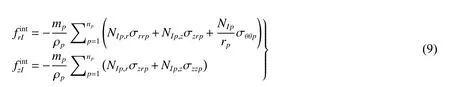
式中：下标p表示质点携带的变量，下标I表示背景网格结点携带的变量；i=r，z；j=r，z；np表示与结点I相邻的质点总数。

1.3 求解格式

在物质点法中，物体的所有物质信息由质点携带，背景网格结点不存储任何物质信息。在求解动量方程时，需要将质点在当前时刻的质量、动量、应力等信息通过形函数映射至背景网格结点，在背景网格上进行求解。之后，将网格结点的速度、位置增量映射回质点，使质点速度、位置得到更新。

物质点法的显式求解方法按照应力更新方式的不同分为先更新应力(update stress first，USF)和后更新应力(update stress last, USL)和改进型USL (modified USL, MUSL)3 种，其中USF 在处理超高速碰撞问题时具有效率高、精度高的特点[10]。

物质点法的USF 求解格式如下：（1）将质点的质量和动量通过形函数映射到背景网格结点，求得结点质量和动量；（2）对结点动量施加边界条件，进行修正；（3）由结点的质量和动量求得结点速度，由此计算质点速度梯度、应变增量和旋量增量，更新质点的体积、应力偏量、内能；（4）通过物态方程求解质点的压力；（5）计算背景网格结点的合力，并根据边界条件进行修正，更新背景网格结点动量；（6）将背景网格结点位置、速度的变化量映射回质点，更新质点的位置和速度；（7）丢弃已变形的网格，在下一时间步使用未变形的新网格。

2 材料模型

材料模型描述了材料在外力作用下的响应。材料模型包括本构模型、失效模型和物态方程。

本构模型用于描述材料的偏应力与偏应变的关系，偏应力更新算法如下式所示[2]：

材料在超高速碰撞过程中的屈服应力可用Johnson-Cook 模型表示[2]：

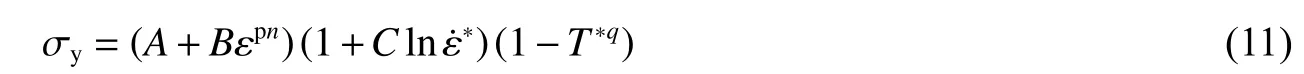
超高速碰撞问题涉及材料的冲击破坏，本文中使用联合失效模型进行描述。当质点的拉应力大于给定值或温度高于熔点时，质点失效。失效质点的应力偏量为零，且不能承受拉应力。

3 新型物态方程的建立

3.1 分子动力学基本原理

分子动力学模拟是一种用来计算多体体系平衡和传递性质的一种确定性方法。分子动力学方法将原子视为经典粒子，体系的多体相互作用由包含经验参数的解析函数直接给出[11]，粒子的运动遵循牛顿运动方程：

式中：mi为粒子i的质量，ri为粒子i的位置矢量，fi为粒子i所受的力，Ep为势函数。

在分子动力学模拟中，势函数表征原子间的相互作用，嵌入原子(embedded atom method，EAM)势在描述金属的性质时与实际情况能够较好地吻合。EAM 势的基本思想是将组成体系的原子看成一个个嵌入由其他所有原子构成的有效介质中的客体原子的集合，从而将系统的总能量表达为嵌入能和相互作用的对势之和[12]。常用的EAM 势有Johnson 分析型EAM 势、Cai-Ye EAM、Zhou EAM 等，本文中采用Cai-Ye EAM 势[12]。EAM 势的总能表达式为：

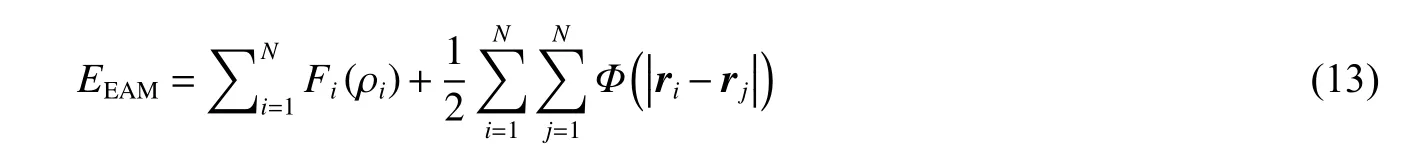
式中：Fi为嵌入项，Φ 为对势项，N为体系粒子数，ρi为粒子i的电荷密度，ri为粒子i的位置矢量，rj为粒子j的位置矢量。

在分子动力学方法中，粒子的微观量与系统的宏观量通过统计物理联系起来。体系的总能量E由下式给出：

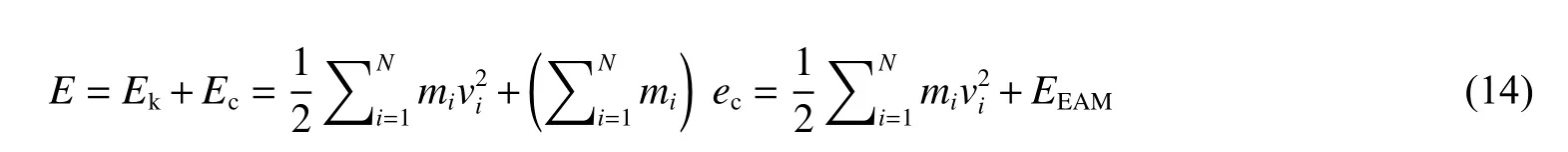
式中：Ek为体系的热能，Ec为体系的冷能，ec为质量冷能，vi为粒子i的速率。

体系的冷压pc可表示为：

式中：V为体系的体积，rij为粒子i与粒子j间的距离，fij为粒子i与粒子j间的作用力。

实际使用中，首先利用分子动力学方法计算得到冷能、冷压与体积比的关系，如图1～2 所示。在超高速碰撞问题的物质点法模拟中，每一时间步内，根据质点当前时刻的体积，利用插值法求得质点的冷能和冷压。

图1 冷能与体积比的关系Fig. 1 Relation between cold energy and volume ratio

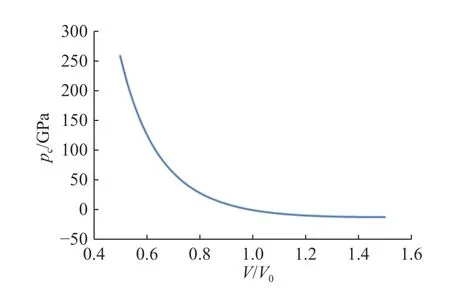
图2 冷压与体积比的关系Fig. 2 Relation between cold pressure and volume ratio

3.2 新型物态方程

新型物态方程基于Grover 定标律方程和分子动力学方法构建，利用分子动力学方法计算冷能、冷压，避免了使用Hugoniot 曲线数据所导致的物态方程形式繁琐。新型物态方程在固-液相区采用Grover 定标律方程的形式，在气相区采用分子动力学中常用的维里方程的形式[13]。针对超高速碰撞问题的物质点法模拟，单个物质点处于单相区或混合相区对整体的影响可忽略不计，因此新型物态方程不考虑混合相区。新型物态方程的形式如下。

当V＜VJ且Ek＜Em（固相）时：

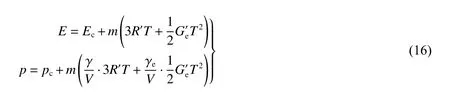
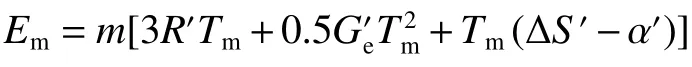
当V＜VJ且Em≤Ek≤EG（液相）时：

当V＜VJ且Ek＞EG（热液相）时：

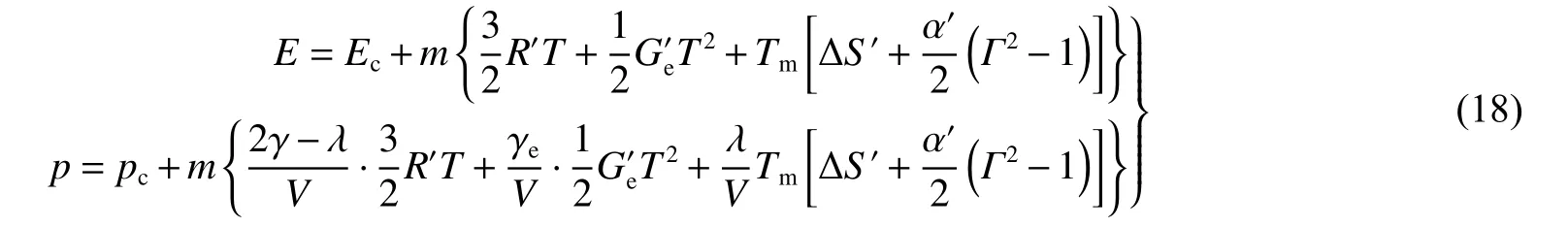
当V≥VJ（气相）时：

3.3 新型物态方程计算流程

在使用新型物态方程的超高速碰撞物质点法模拟中，分子动力学方法用于求解质点的冷能和冷压，质点的热能用于判断所处的相区，具体计算流程如下：

（1）根据物质点法解得的当前时刻质点体积V，得到当前时刻体积V与初始体积V0之比，利用插值法求得质点在当前时刻的冷能Ec和冷压pc，并将体积比代入公式求得Tm、TG、Em、EG；

（2）根据物质点法解得的当前时刻质点内能E，与上一步已求得的冷能Ec，做差求得质点在当前时刻的热能Ek；

（3）根据V、VJ、Ek、Em、EG判断质点所处的相区，利用式(16)～(19)中的能量关系式求得质点温度T，将冷压pc、温度T代入所属相区的压力关系式，求得质点压力p。

4 铝弹铝靶超高速碰撞数值模拟结果

直径为9.5 mm 的球形铝弹丸以6 640 m/s 的超高速撞击厚度为2.2 mm 的铝靶。碰撞6.6 μs 后的实验结果[15]如图3(a)所示, 碎片云长37.7 mm，宽34.2 mm。

弹体和靶体的离散尺寸为0.05 mm，质点总数为58 010，背景网格采用0.1 mm 进行计算，分别使用新型物态方程、Mie-Grüneisen 物态方程、Tillotson 物态方程进行计算，碰撞6.6 μs 后的计算结果如图3(b)～(d)所示。

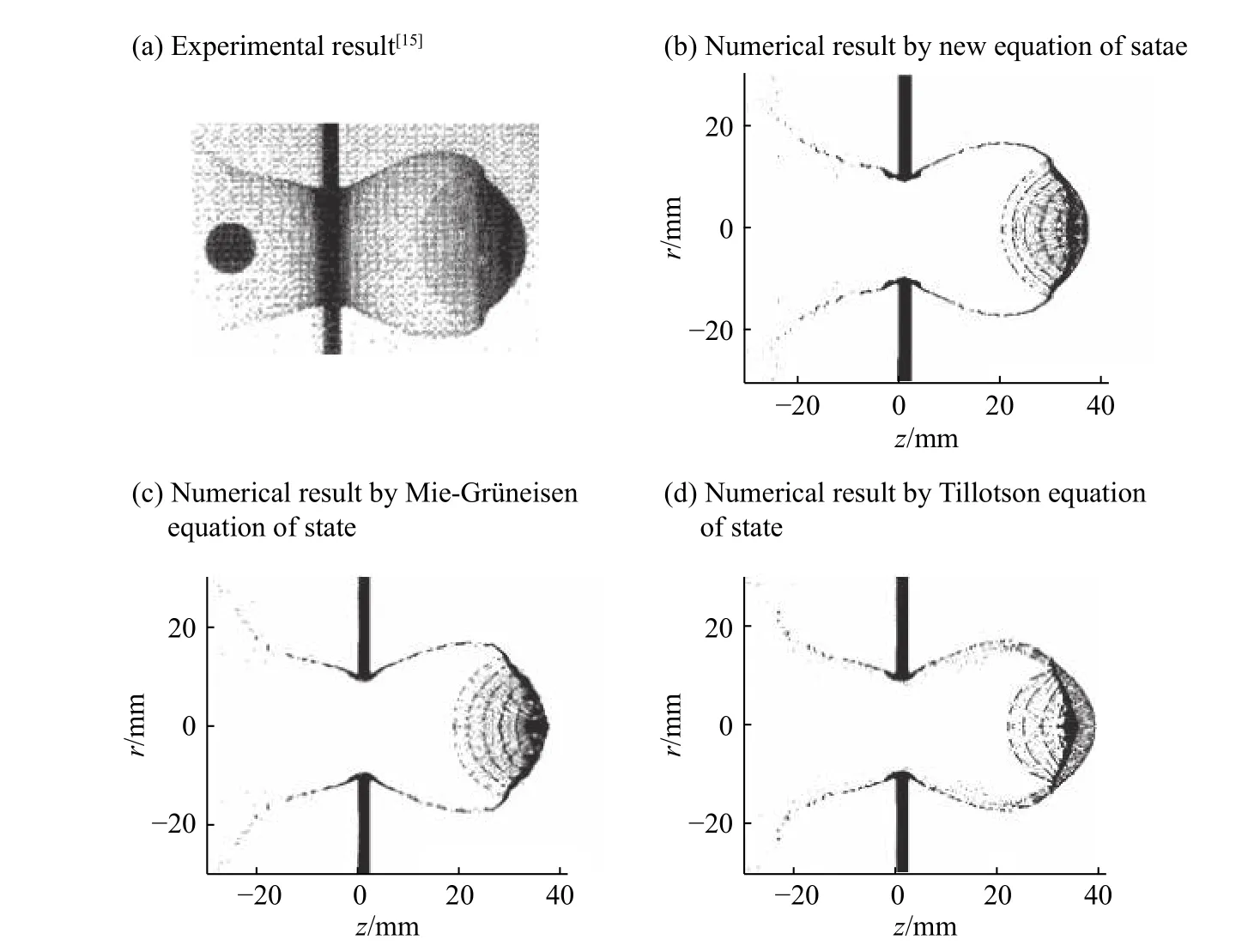
图3 数值模拟结果与实验结果[15]的对比Fig. 3 Comparison between experimental[15] and numerical results

使用新型物态方程计算所得碎片云(图3(b))长36.8 mm，宽33.3 mm，与实验结果[15]符合较好。计算所得碎片云前部呈现出与实验结果相符的阶梯状，碎片云后部反溅部分的形态也与实验结果符合较好。

使用Mie-Grüneisen 物态方程计算所得碎片(图3(c))长36.8 mm，宽32.4 mm。计算所得碎片云前部呈现出阶梯状，但与实验结果[15]存在一定差异，碎片云后部反溅部分的形态与实验结果[15]符合较好。

使用Tillotson 物态方程计算所得碎片(图3(d))长38.7 mm，宽34.1 mm。计算所得碎片云前部没有出现阶梯状，与实验结果[15]不符；碎片云后部反溅部分的形态与实验结果[15]符合较好。

可见，在碎片云尺寸方面，使用3 种物态方程计算结果均与实验结果[15]符合较好。碎片云形态方面，使用新型物态方程计算结果与实验结果最接近；使用Mie-Grüneisen 物态方程计算所得的碎片云前部虽然呈现出阶梯状，但与实验结果[15]仍有差距；使用Tillotson 物态方程计算所得的碎片云前部没有出现阶梯状，形态与实验结果[15]差距最大。

5 结 论

（1）使用柱坐标物质点法能够对轴对称冲击动力学问题进行准确度较高的数值模拟，计算所得碎片云尺寸与实验结果符合较好。（2）尽管Mie-Grüneisen 物态方程只适用于描述金属固体在冲击载荷下的热力学行为，但对于碰撞速度达到6 640 m/s 的超高速碰撞问题，使用Mie-Grüneisen 物态方程计算所得的碎片云尺寸与实验结果相比误差较小，且形态优于使用Tillotson 物态方程的计算结果，因此不必换用Tillotson 物态方程。（3）新型物态方程基于Grover 定标律方程和分子动力学方法建立，可以有效处理材料的相变问题，适用于超高速碰撞问题的分析。使用新型物态方程计算所得的碎片云形态、尺寸与实验结果吻合很好，成功再现铝弹铝靶超高速碰撞碎片云前部的阶梯状形态。（4）使用新型物态方程和Mie-Grüneisen 物态方程计算所得的碎片云尺寸小于实验结果和使用Tillotson 物态方程的计算结果，在使用新型物态方程和Mie-Grüneisen 物态方程对航天器防护结构超高速碰撞进行数值模拟时，有可能因碎片云分布范围小于实际情况而导致不正确的穿透，但有助于提高弹道极限方程的保守性。