半群的(U,V)-区间值模糊子半群
2019-11-15王丰效
王丰效
(喀什大学 数学与统计学院, 新疆 喀什 844000)
模糊集[1]及其理论在许多领域得到了应用。Rosenfeld[2]将模糊集的概念应用于群,引入了模糊子群的概念。作为模糊集的推广,直觉模糊集和区间值模糊集的概念被提出,丰富了模糊集的相关理论。随后,区间值模糊集、直觉模糊集等理论被广泛应用于代数系统[3-4]。半群是一类应用广泛的代数系统,模糊半群理论在模糊语言、模糊码理论、模糊自动机等领域起着重要的作用。Kuroki[5]将模糊集应用于半群,研究了半群的几类模糊理想的特征。谢祥云等[6]详细介绍了模糊半群理论。文献[7-8]分别讨论了半群的反模糊子半群和区间值反模糊子半群的特性。文献[9-10]分别讨论了半群的区间值模糊子半群和区间值模糊理想的相关特性。作为模糊子代数的推广,(λ,μ)-模糊子代数被应用于半群等代数系统[11-12]。本文将(λ,μ)-模糊子代数推广到半群,给出了半群的(U,V)-区间值模糊子半群的概念,并讨论了它的相关特性。
1 预备知识
为了讨论方便,先给出半群以及区间值直觉模糊集的相关概念和性质。
定义1[6]设·是S的一个二元运算,如果对任意x,y∈S有
x·y∈S(2) (x·y)·z=x·(y·z)
则称(S,·)为一个半群。
定义2[8]设A是半群S的模糊集,如果对任意x,y∈S有A(xy)≥A(x)∧A(y),则称A为S的模糊子半群。如果对任意x,y∈S有A(xy)≤A(x)∨A(y),则称A为S的反模糊子半群。
定义3设A是半群S的模糊集,如果对任意x,y∈S有A(xy)∨α≥A(x)∧A(y)∧β,这里 0≤α≤β≤1,则称A为S的(α,β)模糊子半群。
定义4[8]非空集合的区间值模糊集被定义为A=[μA,νA],这里μA和νA分别是X上的模糊集,并且对于任意x∈X,有μA(x)≤νA(x)。
若D[0,1]表示区间[0,1]的闭子区间的全体,对于任意
D1=[a1,b1]∈D[0,1]
D2=[a2,b2]∈D[0,1]
规定
D1≥D2⟺a1≥a2,b1≥b2
D1=D2⟺a1=a2,b1=b2
定义D1与D2的加细极小(记为γmin)和加细极大(记为γmax):
γmin(D1,D2)=[a1∧a2,b1∧b2]
γmax(D1,D2)=[a1∨a2,b1∨b2]
定义5[8]假设(S,·)为一个半群,A=[μA,νA]是S上的区间值模糊集,如果对于任意x,y∈S有A(xy)≥γmin(A(x),A(y)),则称A为半群S的区间值模糊子半群。如果对于任意x,y∈S有A(xy)≤γmax(A(x),A(y)),则称A为半群S的区间值反模糊子半群。
定义6[8]假设(S,·)为一个半群,A是S上的区间值模糊集,D1=[d1,d2]∈D[0,1],称集合
AD1={x∈S|A(x)≥D1}
为区间值模糊集A的D1水平上截集。
2 (U,V)-区间值模糊子半群
为讨论方便,半群(S,·)的二元运算x·y用xy表示,并且约定U≤V。
定义7假设A=[μA,νA]是半群(S,·)上的区间值模糊集,如果对任意x,y∈S和U,V∈D[0,1]都有
γmax(A(xy),U)≥γmin(A(x),A(y),V)
则称A=[μA,νA]是半群(S,·)的(U,V)-区间值模糊子半群。
例1假设S={a,b,c,d},S的二元运算·如下:
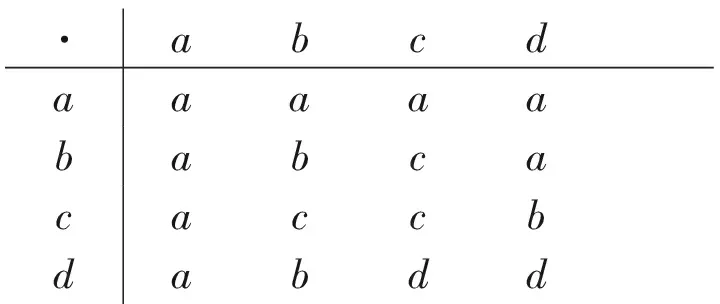
·abcdaaaaababcacaccbdabdd
则(S,·)是半群。定义S上的区间值模糊集A为:
A(a)=[0.7,0.9],A(b)=[0.6,0.7]
A(c)=[0.3,0.5],A(d)=[0.2,0.4]
则A=(μA,νA)为S上的(U,V)-区间值模糊子半群。
定义S上的区间值模糊集B=(μB,νB)为:
B(a)=[0.7,0.9],B(b)=[0.2,0.4]
B(c)=[0.3,0.5],B(d)=[0.7,0.9]
由于
B(cd)=B(b)=[0.2,0.4]≤
[0.3,0.5]=γmin(B(c),B(d))
从而B不是S上的区间值模糊子半群,因而也不是S上的(U,V)-区间值模糊子半群。
定理1半群S的区间值模糊子半群一定是(U,V)-区间值模糊子半群。
证明假设A是半群(S,·)上的区间值模糊子半群,则对任意的x,y∈S有
A(xy)≥γmin(A(x),A(y))
从而对任意的U,V∈D[0,1]有
γmax(A(xy),U)≥A(xy)≥
γmin(A(x),A(y)≥
γmin(A(x),A(y),V)
因此A是半群(S,·)上的(U,V)-区间值模糊子半群。
如果取U=[0,0],V=[1,1],则(U,V)-区间值模糊子半群就是区间值模糊子半群。定理1也表明,半群的(U,V)-区间值模糊子半群的确是区间值模糊子半群的推广。
定理2假设X是半群(S,·)的子半群,则存在半群(S,·)上的(U,V)-区间值模糊子半群A,使得A的上水平截集AD1=X。
证明设X是半群(S,·)的子半群,对于任意的D1∈D[0,1],定义S上的(U,V)-区间值模糊集A满足:如果x∈X,A(x)=D1。如果x∉X,A(x)=[0,0],则有AD1=X。下证A是半群(S,·)上的(U,V)-区间值模糊子半群。分下面几个情况:
1) 若x,y∈X,则xy∈X,因此A(x)=A(y)=A(xy)=D1。因此
γmax(A(xy),U)=γmax(D1,U)≥
γmin(D1,D1,V)=γmin(A(x),A(y),V)
2) 若x∉X或者y∉X,则A(x)=[0,0]或者A(y)=[0,0],从而
γmax(A(xy),U)≥[0,0]=γmin(A(x),A(y),V)
因此对任意的x,y∈S和U,V∈D[0,1]都有
γmax(A(xy),U)≥γmin(A(x),A(y),V)
故A=[μA,νA]是半群(S,·)的(U,V)-区间值模糊子半群。
定理3假设A=[μA,νA]是半群S的(U,V)-区间值模糊集,则A=[μA,νA]是半群S的(U,V)-区间值模糊子半群,当且仅当对任意的D0∈D[0,1],非空集AD0是半群S的子半群。
证明(必要性) 对任意的x,y∈AD0,有A(x)≥D0,A(y)≥D0。由于A=[μA,νA]是半群S的(U,V)-区间值模糊子半群,因此γmax(A(xy),U)≥γmin(A(x),A(y),V),所以对任意U≤D0≤V有
γmax(A(xy),U)≥γmin(A(x),A(y),V)≥D0
即A(xy)≥D0,从而xy∈AD0。故非空集AD0是半群S的子半群。
(充分性) 设对任意的U≤D0≤V,AD0是半群S的子半群。如果存在a,b∈S使得
γmax(A(ab),U)<γmin(A(a),A(b),V)
取区间D满足U≤D≤V和γmax(A(ab),U)
定理4假设A=[μA,νA]是半群S的(U,V)-区间值模糊集,则A=[μA,νA]是半群S的(U,V)-区间值模糊子半群,当且仅当模糊集μA和νA都是半群S的(α,β)模糊子半群。
证明(必要性) 如果A=[μA,νA]是半群S的(U,V)-区间值模糊子半群,则对于任意的x,y∈S
U=[u1,u2],V=[v1,v2]及U,V∈D[0,1]有
γmax(A(xy),U)≥γmin(A(x),A(y),V)
即
[μA(xy)∨u1,νA(xy)∨u2]=
γmax([μA(xy),νA(xy)],[u1,u2])=
γmax(A(xy),U)≥γmin(A(x),A(y),V)=
γmin([μA(x),νA(x)],[μA(y),νA(y)],[v1,v2])=
[μA(x)∧μA(y)∧v1,νA(x)∧νA(y)∧v2]
由区间大小比较的定义有:
μA(xy)∨u1≥μA(x)∧μA(y)∧v1
νA(xy)∨u2≥νA(x)∧νA(y)∧v2
所以模糊集μA和νA都是半群S的(α,β)模糊子半群。
(充分性)模糊集μA和νA都是半群S的(α,β)模糊子半群,则对于任意的x,y∈S,
U=[u1,u2],V=[v1,v2],U,V∈D[0,1]
有:
μA(xy)∨u1≥μA(x)∧μA(y)∧v1
νA(xy)∨u2≥νA(x)∧νA(y)∧v2
因此
γmax(A(xy),U)=[μA(xy)∨u1,νA(xy)∨u2]≥
[μA(x)∧μA(y)∧v1,νA(x)∧νA(y)∧v2]=
γmin(A(x),A(y),V)
由定义7可知A=[μA,νA]是半群S的(U,V)-区间值模糊子半群。
假设A=[μA,νA]和B=[μB,νB]是非空集X的两个区间值模糊集,则A和B的交A∩B也是区间值模糊集,其中A∩B(x)=γmin(A(x),B(x))。
定理5若A=[μA,νA]和B=[μB,νB]都是半群S的(U,V)-区间值模糊子半群,则A和B的交A∩B也是半群S的(U,V)-区间值模糊子半群。
证明如果A=[μA,νA]和B=[μB,νB]都是半群S的(U,V)-区间值模糊子半群,由定理4可知μA和νA,μB和νB都是半群S的(α,β)模糊子半群,从而对于x,y∈S以及0≤u1≤v1≤1,0≤u2≤v2≤1,有
μA(xy)∨u1≥μA(x)∧μA(y)∧v1
νA(xy)∨u2≥νA(x)∧νA(y)∧v2
μB(xy)∨u1≥μB(x)∧μB(y)∧v1
νB(xy)∨u2≥νB(x)∧νB(y)∧v2
因此
μA∩B(xy)∨u1=(μA(xy)∧μB(xy))∨u1=
(μA(xy)∨u1)∧(μB(xy)∨u1)≥
(μA(x)∧μA(y)∧v1)∧(μB(x)∧μB(y)∧v1)=
(μA(x)∧μA(y))∧(μB(x)∧μB(y))∧v1=
(μA(x)∧μB(x))∧(μA(y)∧μB(y))∧v1=
μA∩B(x)∧μA∩B(y)∧v1
νA∩B(xy)∨u2=(νA(xy)∧νB(xy))∨u2=
(νA(xy)∨u2)∧(νB(xy)∨u2)≥
(νA(x)∧νA(y)∧v2)∧(νB(x)∧νB(y)∧v2)=
(νA(x)∧νA(y))∧(νB(x)∧νB(y))∧v2=
(νA(x)∧νB(x))∧(νA(y)∧νB(y))∧v2=
νA∩B(x)∧νA∩B(y)∧v2
因此,μA∩B和νA∩B都是半群S的(α,β)模糊子半群。由定理4可得A∩B也是半群S的(U,V)-区间值模糊子半群。
推论1若A=[μA,νA]和B=[μB,νB]都是半群S的(U,V)-区间值模糊子半群,则μA∩B和νA∩B都是半群S的(α,β)模糊子半群。
下面讨论半群的(U,V)-区间值模糊子半群直积的性质。假设S和R是两个半群,A和B分别是S和R上的区间值模糊集,定义S×R上的区间值模糊集A×B为
A×B(x,y)=γmin(A(x),B(y)),
(x,y)∈S×R
定理6假设A和B分别是半群S和R上的(U,V)-区间值模糊子半群,则A×B是半群S×R的(U,V)-区间值模糊子半群。
证明对于任意的(x1,y1),(x2,y2)∈S×R,有
A×B((x1,y1)(x2,y2))=A×B(x1x2,y1y2)=
γmin(A(x1x2),B(y1y2))
由于A和B分别是半群S和R上的(U,V)-区间值模糊子半群,因此:
γmax(A(x1x2),U)≥γmin(A(x1),A(x2),V)
γmax(B(y1y2),U)≥γmin(B(y1),B(y2),V)
故
γmax(A×B(x1x2),U)=
γmax(γmin(A(x1x2),B(y1y2)),U)=
γmin(γmax(A(x1x2),U),γmax(B(y1y2),U))≥
γmin(γmin(A(x1),A(x2),V),γmin(B(y1),B(y2),V))=
γmin(γmin(A(x1),A(x2)),γmin(B(y1),B(y2)),V)=
γmin(γmin(A(x1),B(y1)),γmin(A(x2),B(y2)),V)=
γmin(A×B(x1,y1),A×B(x2,y2),V)
因此A×B是半群S×R的(U,V)-区间值模糊子半群。
推论2假设A是半群S上的(U,V)-区间值模糊子半群,则A×A是半群S×S的(U,V)-区间值模糊子半群。
定理7假设A×B是半群S×R的(U,V)-区间值模糊子半群,则A1和B1分别是S和R的(U,V)-区间值模糊子半群,其中:
A1(x)=γmax{A×B(x,z)|z∈R}
B1(y)=γmax{A×B(z,y)|z∈S}
证明仅证明A1是S的(U,V)-区间值模糊子半群,B1是R的(U,V)-区间值模糊子半群,可类似证明。由于A×B是半群S×R的(U,V)-区间值模糊子半群,所以μA∩B和νA∩B都是半群S的(α,β)模糊子半群。因为A1(x)=γmax{A×B(x,z)|z∈R},所以:
μA1(x)=supz∈R(μA×B(x,z))
νA1(x)=supz∈R(νA×B(x,z))
只需证明μA1(x)和νA1(x)都是半群S的(α,β)模糊子半群。对任意的x1,x2∈S有:
μA1(x1x2)∨u1=supz∈R(μA×B(x1x2,z))∨u1=
supz1,z2∈R(μA×B(x1x2,z1z2))∨u1=
supz1,z2∈R(μA×B(x1,z1)(x2,z2)∨u1)≥
supz1,z2∈R(μA×B(x1,z1)∧μA×B(x2,z2)∧v1)=
supz1∈R(μA×B(x1,z1))∧
supz2∈R(μA×B(x2,z2))∧v1=
μA1(x1)∧μA1(x2)∧v1
νA1(x1x2)∨u2=supz∈R(νA×B(x1x2,z))∨u2=
supz1,z2∈R(νA×B(x1x2,z1z2))∨u2=
supz1,z2∈R(νA×B(x1,z1)(x2,z2)∨u2)≥
supz1,z2∈R(νA×B(x1,z1)∧νA×B(x2,z2)∧v2)=
supz1∈R(νA×B(x1,z1))∧supz2∈R(νA×B(x2,z2))∧v2=
νA1(x1)∧νA1(x2)∧v2
因此μA1(x)和νA1(x)都是半群S的(α,β)模糊子半群,从而由定理4可知A1是S的(U,V)-区间值模糊子半群。
最后讨论半群的(U,V)-区间值模糊子半群的同态像和原像的相关性质。假设(S,·)和(R,·)是两个半群,称f:S→R为从S到R的同态,如果对于任意的x,y∈S,有f(xy)=f(x)f(y)。
定理8假设(S,·)和(R,·)是两个半群,f为从S到R的同态满射。如果B是半群R的(U,V)-区间值模糊子半群,则B的原像f-1(B)是半群S的(U,V)-区间值模糊子半群。这里
f-1(B)(x)=B(f(x))
证明由于f为从S到R的同态满射,所以对于任意的x1,x2∈S,存在y1,y2∈R使得f(x1)=y1,f(x2)=y2。因为B是半群R的(U,V)-区间值模糊子半群,从而有
γmax(B(y1y2),U)≥γmin(B(y1),B(y2),V)
因此
γmax(f-1(B)(x1x2),U)=γmax(B(f(x1x2)),U)=γmax(B(f(x1)f(x2)),U)=
γmax(B(y1y2),U)≥γmin(B(y1),B(y2),V)=
γmin(B(f(x1)),B(f(x2)),V)=
γmin(f-1(B)(x1),f-1(B)(x2),V)
故B的原像f-1(B)是半群S的(U,V)-区间值模糊子半群。
推论3假设(S,·)和(R,·)是两个半群,f为从S到R的同态满射。如果B是半群R的(U,V)-区间值模糊子半群,则f-1(μB)和f-1(νB)是半群S的(α,β)模糊子半群。
定理9假设(S,·)和(R,·)是两个半群,f为从S到R的同态满射。如果A是半群S的(U,V)-区间值模糊子半群,则f(A)是半群R的(U,V)-区间值模糊子半群。这里
f(A)(y)=γmax(A(x)|f(x)=y)。
证明对于任意的y1,y2∈R,由于f为从S到R的同态满射,从而存在x1,x2∈S使得f(x1)=y1,f(x2)=y2。因A是半群S的(U,V)-区间值模糊子半群,从而:
γmax(A(x1x2),U)≥γmin(A(x1),A(x2),V)
γmax(f(A)(y1y2),U)=
γmax(γmax(A(x1x2)|f(x1x2)=y1y2),U)=
γmax(γmax(A(x1x2)|f(x1)=y1,f(x2)=y2),U)=
γmax(γmax(A(x1x2),U)|f(x1)=y1,f(x2)=y2)≥
γmax(γmin(A(x1),A(x2),V)|f(x1)=y1,f(x2)=y2)≥
γmin(γmax(A(x1)|f(x1)=y1)
γmax(A(x2)|f(x2)=y2),V)≥
γmin(f(A)(y1),f(A)(y2),V)
所以f(A)是半群R的(U,V)-区间值模糊子半群。
3 结束语
本文引入了半群的(U,V)-区间值模糊子半群的概念,讨论了半群的(U,V)-区间值模糊子半群的相关性质。(U,V)-区间值模糊子半群的概念推广了带限制(α,β)的模糊子半群的概念,丰富了模糊子半群的相关理论。同样,带限制(U,V)的区间值模糊子代数的概念也可以类似地应用于其他代数系统,如坡代数、布尔代数等。下一步将研究和讨论半群的(U,V)-区间值模糊理想,(U,V)-区间值模糊双理想以及半群的(U,V)-区间值模糊内理想的相关特性。
