污染物对具有Allee效应的水生种群的影响
2019-11-15任建录温金秋
任建录,温金秋
(西南大学 数学与统计学院, 重庆 400715)
环境污染是影响生态系统健康的重要因素,长期以来受到人们的广泛关注。随着工业的发展,工业污染物(石油碳氢化合物、重金属和杀虫剂等)排放到水生环境中会对水生物种的生长和繁殖造成严重的影响。因此,降低环境中的毒素已经成为环境保护的重要举措。为了保护生态环境和水生物种,有必要评估水生群落对毒素的敏感性[1-3],并找出决定生物体持续生存和灭绝的相关因素。近些年来,为了研究环境污染物对生物个体和种群乃至整个生态系统的影响机理,相关学者建立了很多数学模型[4-6],包括常微分方程模型、差分方程等,但已有的常微分方程考虑的种群通常被假设为logistic增长。然而在现实世界中,种群都有自己的最适密度,过分稀疏和过分密集都会导致种群的负增长,这就是生态学中著名的Allee效应。
本文主要做了以下工作:① 建立具有Allee效应且受毒素影响的种群动力学模型。② 对模型进行稳定性分析,并且获得确保种群持续生存的条件。③ 利用Matlab软件进行数值模拟,进一步验证理论分析的结果。
1 模型建立
考虑水圈中受污染物影响的水生种群,首先定义几个重要的模型状态变量或参数。
x(t)=种群生物量的浓度=
Tp(t)=种群体内毒素的浓度=
Te(t)=环境中的毒素的浓度=
y(t)=单位质量的种群的所含的毒素总量=
为了研究环境中的毒素对种群动力学行为的影响,建立以下模型,
其中参数b、β、K、K0、q、m、Te、σ均为正常数,在表1中列举了各个变量和参数的含义及单位。

表1 各个变量和参数的单位和含义
第1个式子描述种群生物量在毒素影响下的变化率。bx/(1+βy)(1-x/K)(x/K0-1)表示种群在毒素影响下的增长率;bx/(1+βy)表示种群增长率随毒素的升高而递减;1-x/K表示种群的增长率受到环境容纳量的影响;x/K0-1表示种群受到Allee效应影响。(qy+m)x表示种群在毒素影响下的死亡率。若没有毒素影响,即y=0时,种群死亡率即为自然死亡率m。
第2个式子描述了种群体内的毒素随时间的变化率。axTe表示种群从环境中吸收的毒素;σTp表示种群对毒素的自我净化;(qy+m)Tp表示种群死亡带走的毒素;Te的变化取决于种群的死亡和代谢、外部的毒素、太阳光分解或水解等条件。然而在实际中,个体的死亡和代谢过程对环境中的毒素的影响几乎可以忽略。因此,为了简化分析,在本文中将Te作为一个参数。
最后一个式子中,Tp/x表示单位质量的种群体内所包含的毒素量。
由于毒素对种群生长的直接影响可直接由单位质量的种群体内所含的毒素总量y(t)来实现, 所以系统中的3个方程组可归结为一个由两个微分方程组成的系统。利用链式法则,对最后一个方程关于t进行微分得到y(t)关于时间t的变化率。
因此,本文主要研究微分方程系统(1)。
(1)
2 平衡点的存在性和局部稳定性
为简化问题,便于分析,对方程进行量纲为一化,引入以下的变量和参数:
忽略“~”,系统(1)简化为:
(2)
本文假设这些参数q、m、σ、T都是非负的。且0
2.1 解的非负性和有界性
定理1在初始条件为x(0)≥0和y(0)≥0时,系统(2)的任何解都将落入矩形区域Ω中,有
证明系统在Ω内是局部Lipschitz-连续的,这保证了解的存在性和唯一性。
当x=0时,dx/dt=0。当x=1/K时,dx/dt<0。当y=0时,dy/dt=0。当y=(T+1)/σ时,dy/dt<0。因此,所有从Ω开始的轨道都不能脱离它的边界,初始条件为x(0)≥0和y(0)≥0的系统的轨线将进入和停留在矩形区域Ω。
2.2 平衡点的存在性
首先考虑系统(2)边界平衡点的存在性, 令dx/dt=0和dy/dt=0可得到平衡方程。
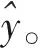
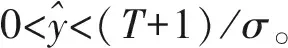
接下来考虑系统(2)的正平衡点的存在性,一个内平衡点即为以下方程的正解:
解得
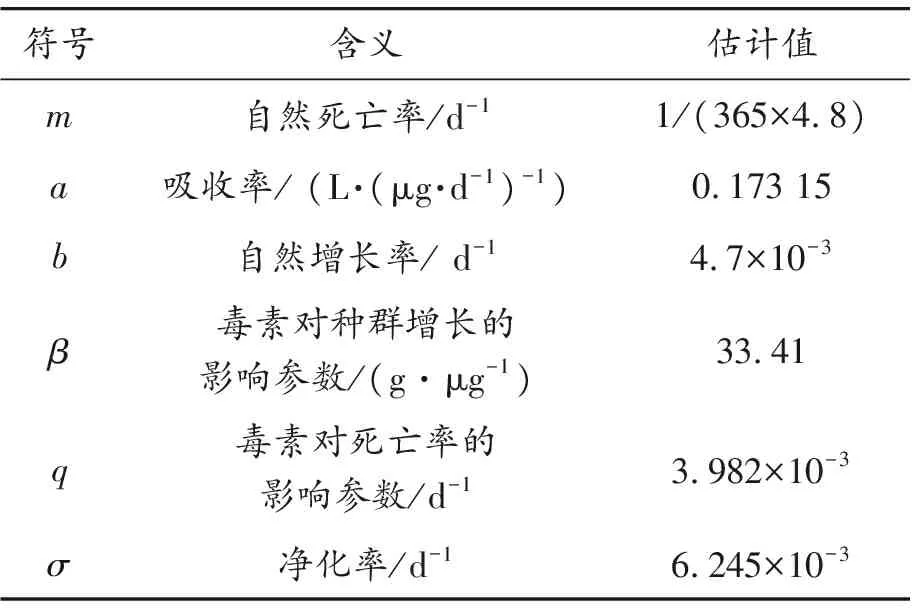
其中Y*=(qy*+m)(1+y*)。
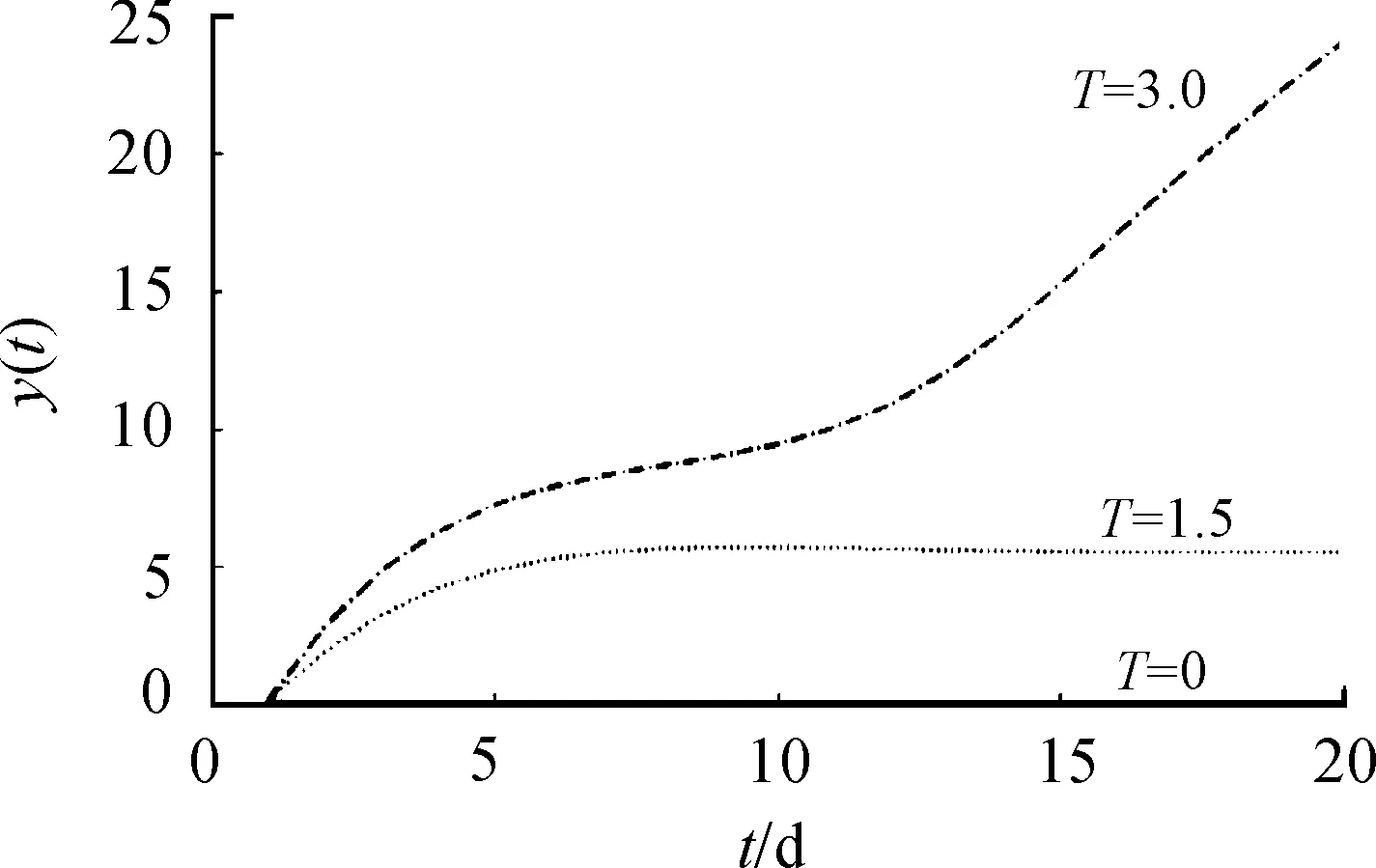
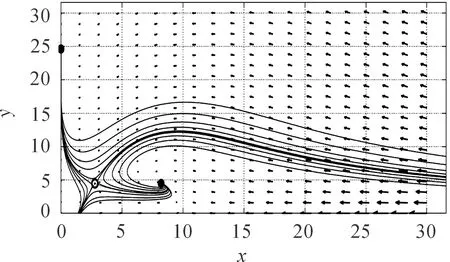
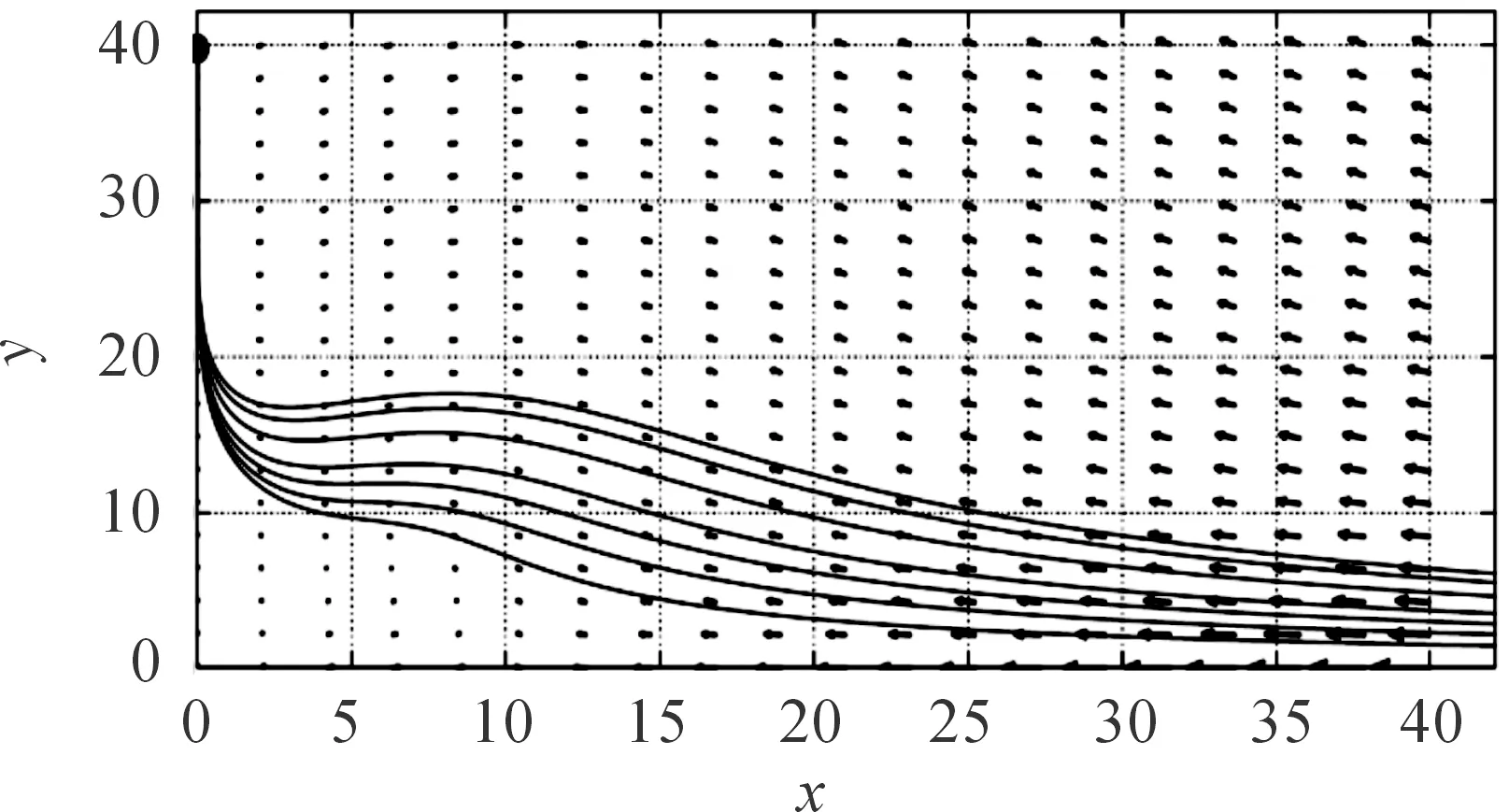
容易验证,0 对于不等式 qy*2+ (q+m)y*+m-s< 0 计算可知m 将第2个不等式整理为T的不等式,从而可得 根据上述讨论,发现边界平衡点总是存在的。 正平衡点存在,当且仅当自然死亡率m小于s且环境中毒素浓度T小于临界值Tc。在死亡率函数的表达式中,Tc依赖于m、q、K。 定理2对于系统(2),有 证明系统(2)的Jacobi矩阵为 这里 下面将边界平衡点和内平衡点依次代入。 则特征值为: 本文以文献[7]中甲基汞对虹鳟鱼的影响为例,利用本文建立的模型进行数值模拟,进一步验证上述结论。将表2的参数转化为量纲为一化后的参数值为: q≈0.025 4,m≈0.121 4,σ≈0.1,K≈0.1 图1 t-x(t) 图4为当T=3.0>Tc≈2.50时,在矩形区域内仅有一个稳定的边界平衡点,即外界毒素水平过高,种群的死亡率远远大于增长率,最终只能走向灭亡。 图2 t-y(t) 图3 x(t)-y(t)(T=1.5) 图4 x(t)-y(t)(T=3.0) 本文研究了一个具有Allee效应且受毒素影响的水生种群模型的动力学行为。当外界毒素小于阈值时,种群初始密度大于一定值时将会持续生存,种群初始密度小于一定值时将会灭绝。然而当毒素大于阈值时种群将趋于灭绝。但模型中尚未考虑毒素在种群体内的作用时间,以及幼年和成熟期对毒素不同的净化能力。后一阶段将增加年龄结构和时滞,进一步改进模型,使其更加具有现实意义。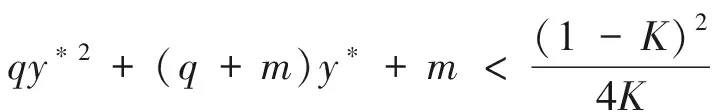
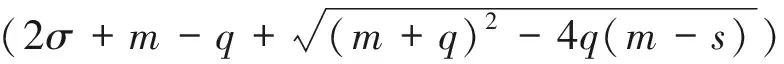
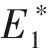
2.3 平衡点的局部稳定性
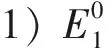
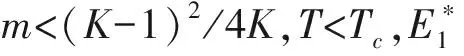
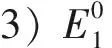
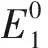
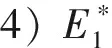
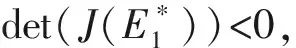

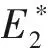
3 数值模拟
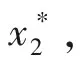
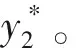
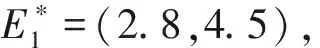
4 结束语
