无金标准部分核实数据下基于风险差的等价性检验

邱世芳，何 杰

(重庆理工大学 理学院， 重庆 400054)

在流行病学研究中，为了估计某种疾病的流行率，常使用价格便宜的筛检方法对个体进行第一次诊断。由于筛检方法常存在误判，从而导致基于有误判数据的估计常常是有偏的[1]。在实际中，完全的金标准是不存在的，同时其花费很高且非常耗时。为此，Tenenbein[2]提出了二重抽样方法，即从感兴趣的总体中随机抽取N个个体接受易犯错的分类器分类，再从中随机抽取n个个体接受金标准检验。这种方法叫作二重抽样方法，得到的数据称为部分核实数据[3]。

基于Tenenbein[2]提出的二重抽样方法得到的部分核实数据，Tang等[3]研究了单个总体下的疾病流行率的假设问题，考虑了基于Score检验、似然比检验以及2种Wald型检验的大样本渐近的检验过程以及小样本近似非条件检验过程；Tang等[4]基于上述检验统计量提出了关于疾病流行率的12种区间估计方法；并从显著性检验的角度和区间估计的角度考虑了样本量的确定方法[5]；对于2组样本情形，Tang等[6]基于比例差考虑了2组疾病流行率的显著性差异的假设检验过程，以及从检验功效的角度研究了样本量的确定问题；同时，Qiu等[7]考虑了2组样本下关于疾病流行率差的区间估计方法，从置信区间的角度研究了2组样本的疾病流行率的显著性差异问题。

以上研究中有一个重要的假定是存在一种完全无误判的金标准。但在实际应用中，完全准确的金标准检验也许根本不存在。为此，安金兵等[8]考虑了在无金标准条件下的诊断试验；Qiu等[9]在2种分类器都有误判的情况下，基于单组样本下的部分核实数据考虑了基于疾病流行率的假设检验过程以及样本量的确定，以及邱世芳等[10]从区间估计的角度研究了在给定置信水平下区间宽度控制下的样本量的估计问题。但Qiu等[9-10]只考虑单组样本下的部分核实数据对疾病流行率的显著性检验过程。而实际生活中，疾病流行率可能会受到年龄、生活习惯等的影响。为此，本文在此基础上进一步考虑2组独立的无金标准部分核实数据下基于风险差的显著性检验问题。

1 数据结构

在2种分类器都有误判的情况下，假设从第j组感兴趣总体中随机抽取了Nj个个体进行初级分类器(J)分类，再从Nj个个体中随机抽取nj个个体进行高级分类器(S)分类，得到频数为nikj(i,k=0,1,j=1,2)。其中，Nj-nj个个体只接受了初级分类器的分类；xj表示检验为阳性的个体数；yj表示检验为阴性的个体数，数据结构由表1所示。

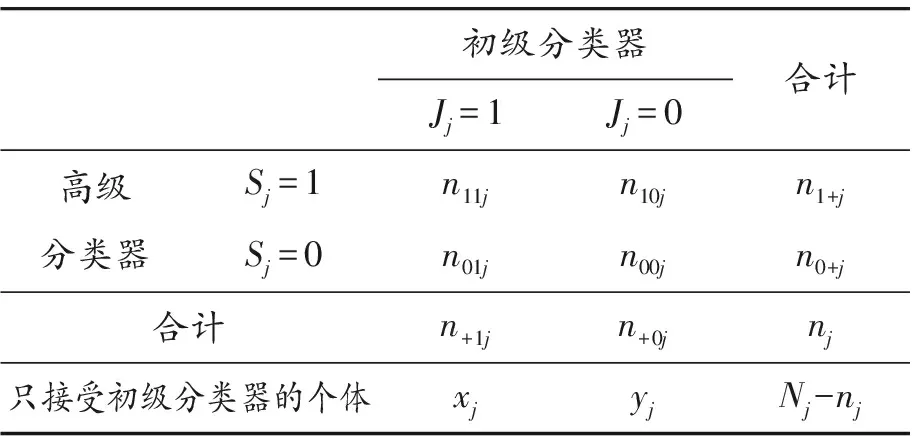
表1 第j组的数据结构

令Dj=1表示患病，Dj=0表示不患病，Jj=1表示初级分类器诊断个体呈阳性，反之Jj=0；Sj=1表示高级分类器诊断个体呈阳性，反之Sj=0。令πj=P(Dj=1)为第j组感兴趣总体真实的患病率，ηj=P(Jj=1|Dj=1)和θj=P(Sj=1|Dj=1)分别表示第j组样本下初级分类器和高级分类器的敏感度。本文假定两种分类器都不存在假阳性。

2 假设检验

本文感兴趣的问题是如下的假设检验：

H0:π1=π2↔H1:π1≠π2

令δ=π2-π1，上述的假设检验就可变为：

H0:δ=0↔H1:δ≠0

2.1 模型1和检验统计量

假定初级分类器和高级分类器的分类结果是条件独立的，即满足P(Jj,Sj|Dj)=P(Jj|Dj)P(Sj|Dj),j=1,2。在此假定下，可得如下的概率模型(Nedelman[11])，其概率分布如表2所示。

表2 第j组的概率分布

令m={(n11j,n10j,n01j,n00j,xj,yj):j=1,2}为观测数据，则观测数据m的对数似然函数为：

l1(m;π1,δ,η1,θ1,η2,θ2)=

n01j+xj)logηj+n10jlog(1-ηj)+

(n11j+n10j)logθj+n01jlog(1-θj)+

n00jlog[1-πj(ηj+θj-ηjθj)]+

yjlog(1-πjηj)}

(1)

其中，π2=π1+δ；C1是一个与参数无关的常数。

简单计算可得π1、δ、ηj、θj(j=1,2)的非限制性极大似然估计，分别为：

(2)

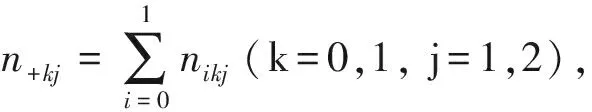
(3)

在H0:δ=0下，π1的限制性极大似然估计为：

(4)

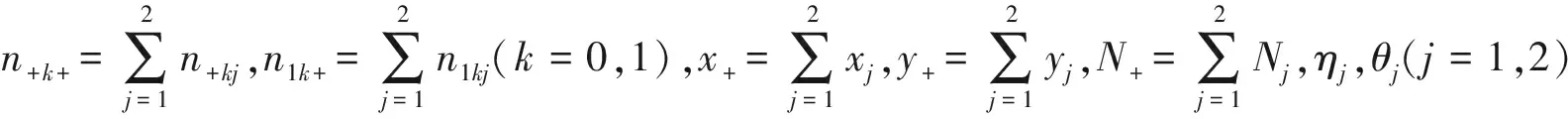
(5)

此方程组的解没有显表达式，可用迭代方法如牛顿迭代法求解。

2.1.1Wald型检验统计量

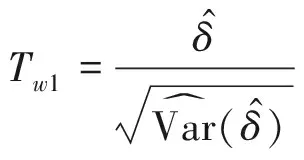
在原假设H0:δ=0下，当N1和N2趋近无穷大时，Tw1和Tw2的渐近分布为标准正态分布。

2.1.2似然比检验统计量

根据式(1)给出的对数似然函数，对于假设检验H0:δ=0↔H1：δ≠0有如下的似然比检验统计量：

在原假设H0:δ=0下，当N1和N2趋近无穷大时，Tl的渐近分布为自由度为1的卡方分布。

2.1.3Score检验统计量

根据Rao[12]提出的score理论，对于假设检验H0:δ=0↔H1：δ≠0，经过推导得到如下的score检验统计量：

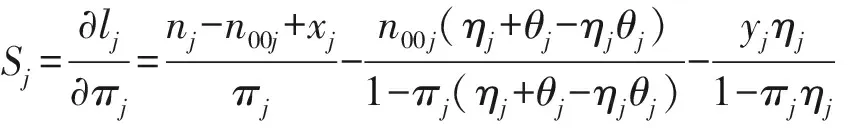
2.1.4基于反双曲正切变换的检验统计量

和

在原假设H0:δ=0下，当N1和N2趋近无穷大时，Ttan1和Ttan2的渐近分布为标准正态分布。

2.2 模型2和检验统计量

假定初级分类器和高级分类器存在假阳性且条件不独立时，根据Lie[13]提出的模型，其概率分布如表3所示。

表3 第j组的概率分布

注：j=1,2

观测样本m的对数似然函数为：

l2(m;π1,δ,η1,θ1,η2,θ2)=

C2+(nj-n00j+xj)log(πj)+

n00jlog(1-πj)+xjlogηj+

n10jlog(1-ηj)+n01jlog(1-θj)+

yjlog(1-πjηj)+n11jlog(ηj+θj-1)

(6)

其中：π2=π1+δ；C2是一个与参数无关的常数。

经过简单计算，可得π1,δ,ηj,θj(j=1,2)的非限制性极大似然估计，分别为：

(7)

(8)

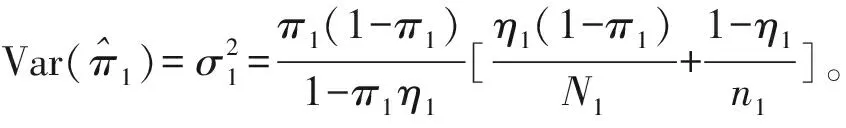
在H0:δ=0下，π1的限制性极大似然估计为：

(9)

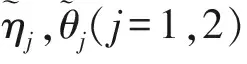
由此，得到如下的估计：

(10)

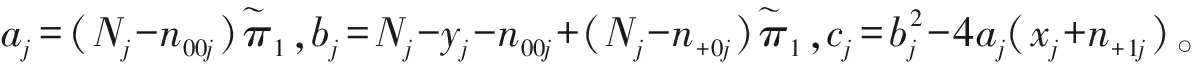
2.2.1Wald型检验统计量

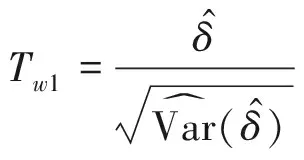
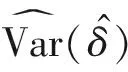
2.2.2似然比检验统计量

由式(6)可得到如下的似然比检验统计量：

在原假设H0:δ=0下，当N1和N2趋近无穷大时，Tl的渐近分布为自由度为1的卡方分布。

2.2.3Score检验统计量

在原假设H0:δ=0成立下，可以得到Score检验统计量：

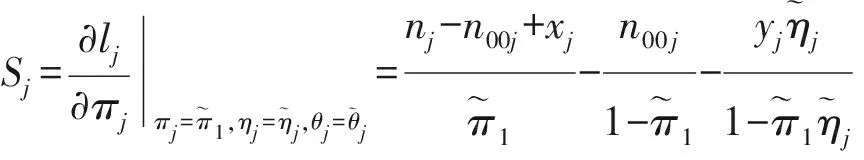
2.2.4基于反双曲正切变换的检验统计量

同模型1，可以得到2种反双曲正切逆变换的检验统计量：

和

在原假设H0:δ=0下，当N1和N2趋近无穷大时，Ttan1和Ttan2的渐近分布为标准正态分布。

3 模拟研究

为评估Tw1、Tw2、Tsc、Tl、Ttan1和Ttan2检验方法的有效性，考虑了如下样本量的模拟研究：① 小样本：(n1,n2,N1,N2)=(20,20,30,30),(30,30,50,50)；② 中等样本(n1,n2,N1,N2)=(50,50,100,100)；③ 大样本：(n1,n2,N1,N2)=(200,200,500,500)。

在不同的样本量设置下，考察犯第一类错误的概率时考虑了如下参数设置：π1=0.1(0.2)0.5，η1=0.5(0.1)0.7，θ1=0.7(0.1)0.9，η2=η1+0.05，θ2=θ1+0.05，即考虑了3(π1的值)×3(η1(η2)的值)×3(θ1(θ2)的值)=27种参数组合。对于检验功效考虑了：δ=0.1(0.01)0.3，π1=0.1(0.2)0.5，(η1,θ1)=(0.5,0.7),(0.6,0.8),(0.7,0.9)，η2,θ2同以上设置，即考虑了3(δ的值)×3(π1的值)×3((η1,θ1)的值)=27种参数组合。这里的a(b)c表示取值是从a以步长b变化到c。在每个样本量设置和每种参数设置下，随机产生5 000组数据m={(n11j,n10j,n01j,n00j,xj,yj):j=1,2}，在显著性水平α=0.05下，对于每个检验统计量Ti(i=w1,w2,sc,l,tan1,tan2)，其犯第一类错误的概率可通过以下公式计算：基于统计量Ti拒绝原假设的次数/5 000(δ=0)，经验功效通过以下公式计算基于统计量Ti拒绝原假设的次数/5 000(δ≠0)。犯第一类错误概率的模拟结果见表4～7。由于篇幅的限制，只列出了小样本和中等样本下的部分功效的模拟结果，见表8～9。

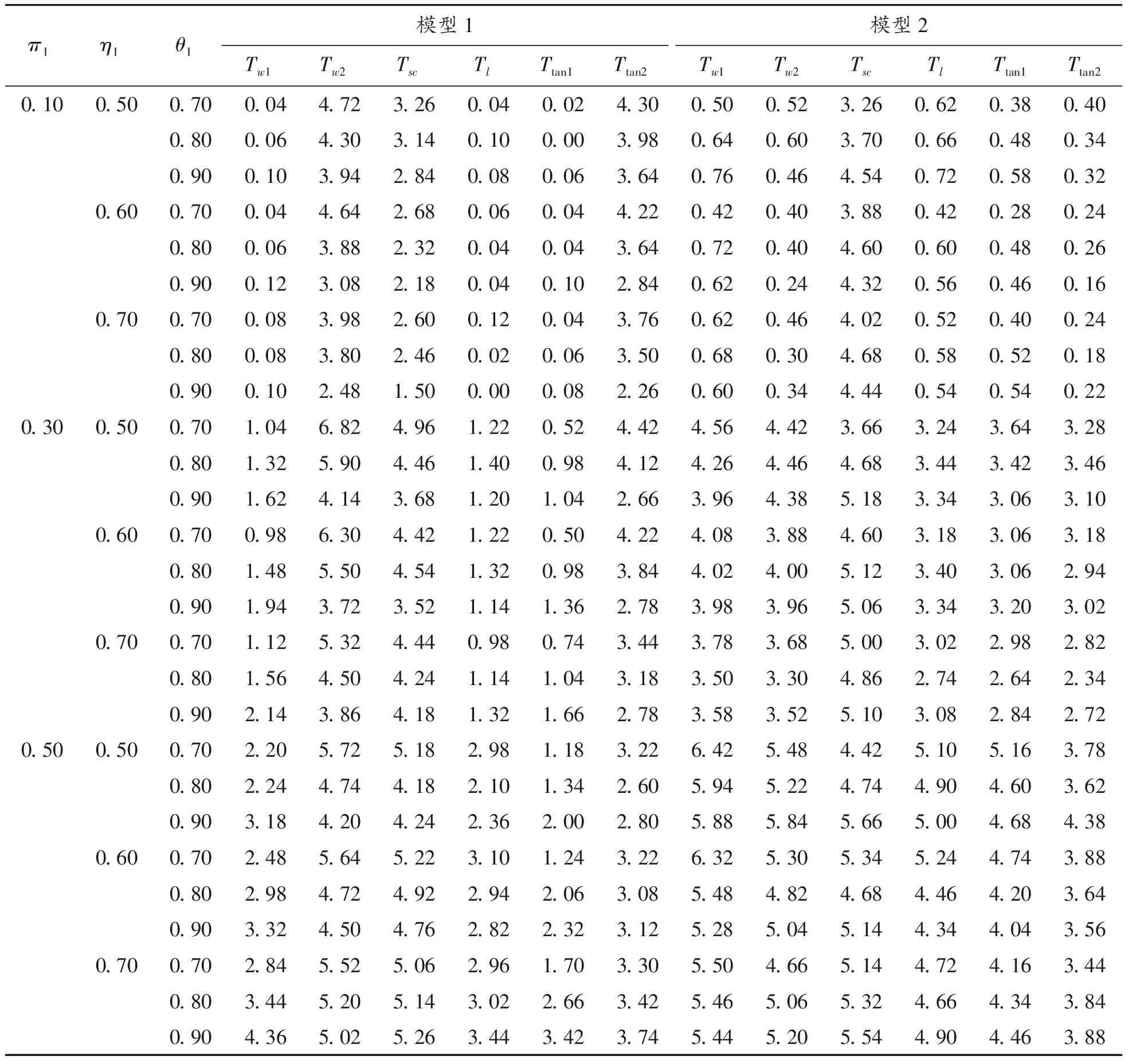
表4 小样本(n1,n2,N1,N2)=(20,20,30,30)下犯第一类错误的概率(显著性水平α=0.05)

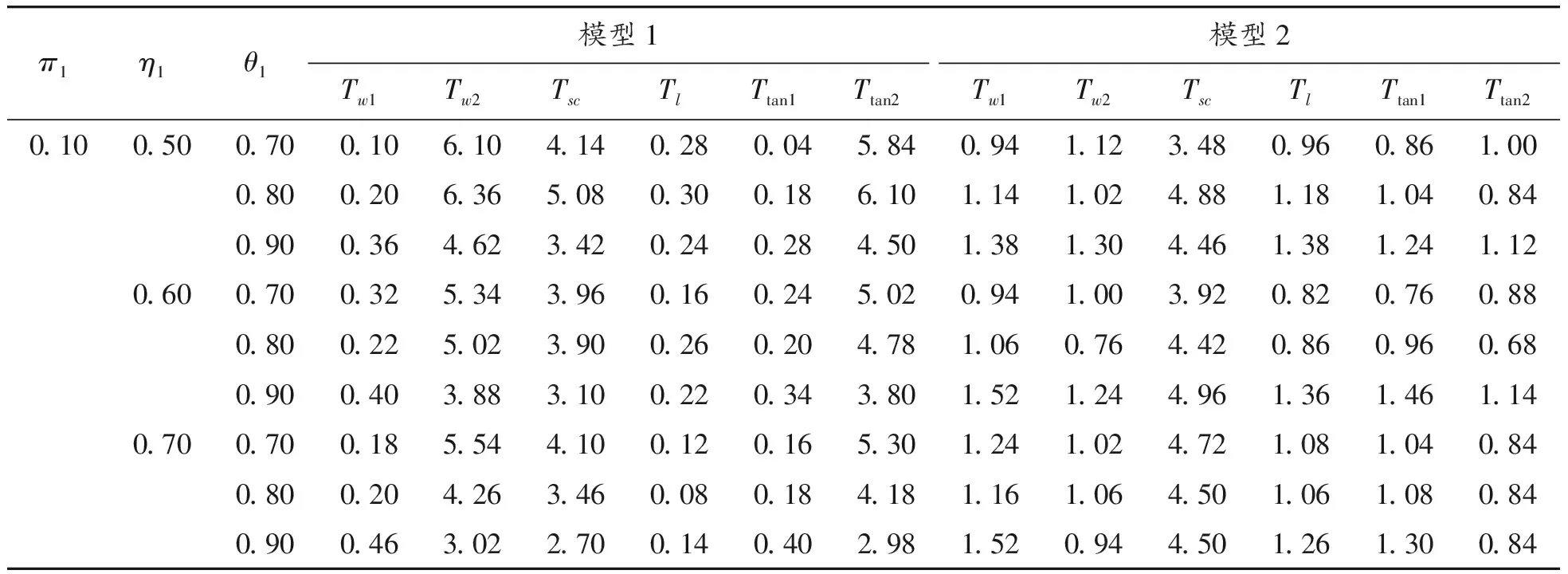
表5 小样本(n1,n2,N1,N2)=(30,30,50,50)下犯第一类错误的概率(显著性水平α=0.05)

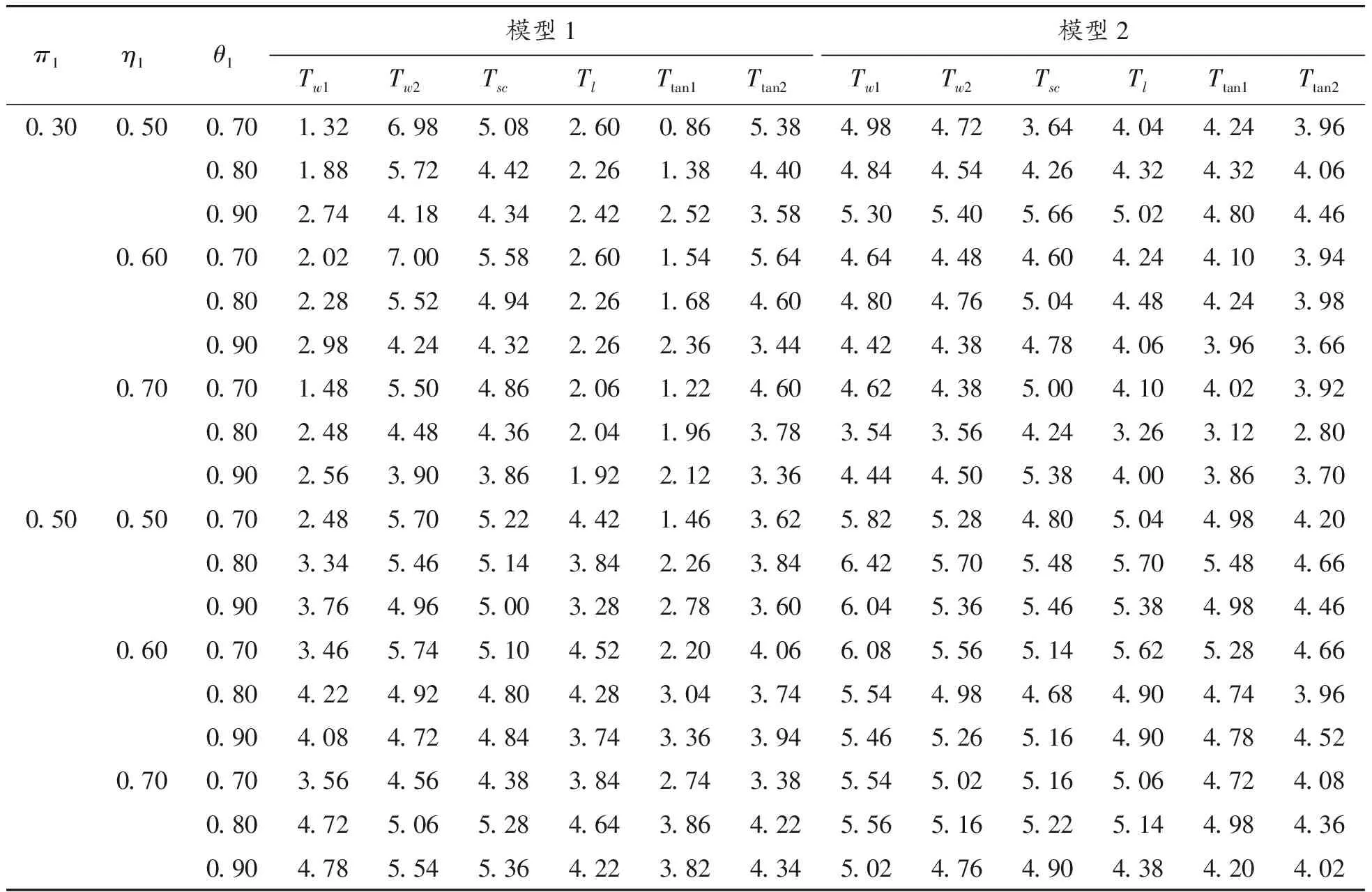
续表(表5)

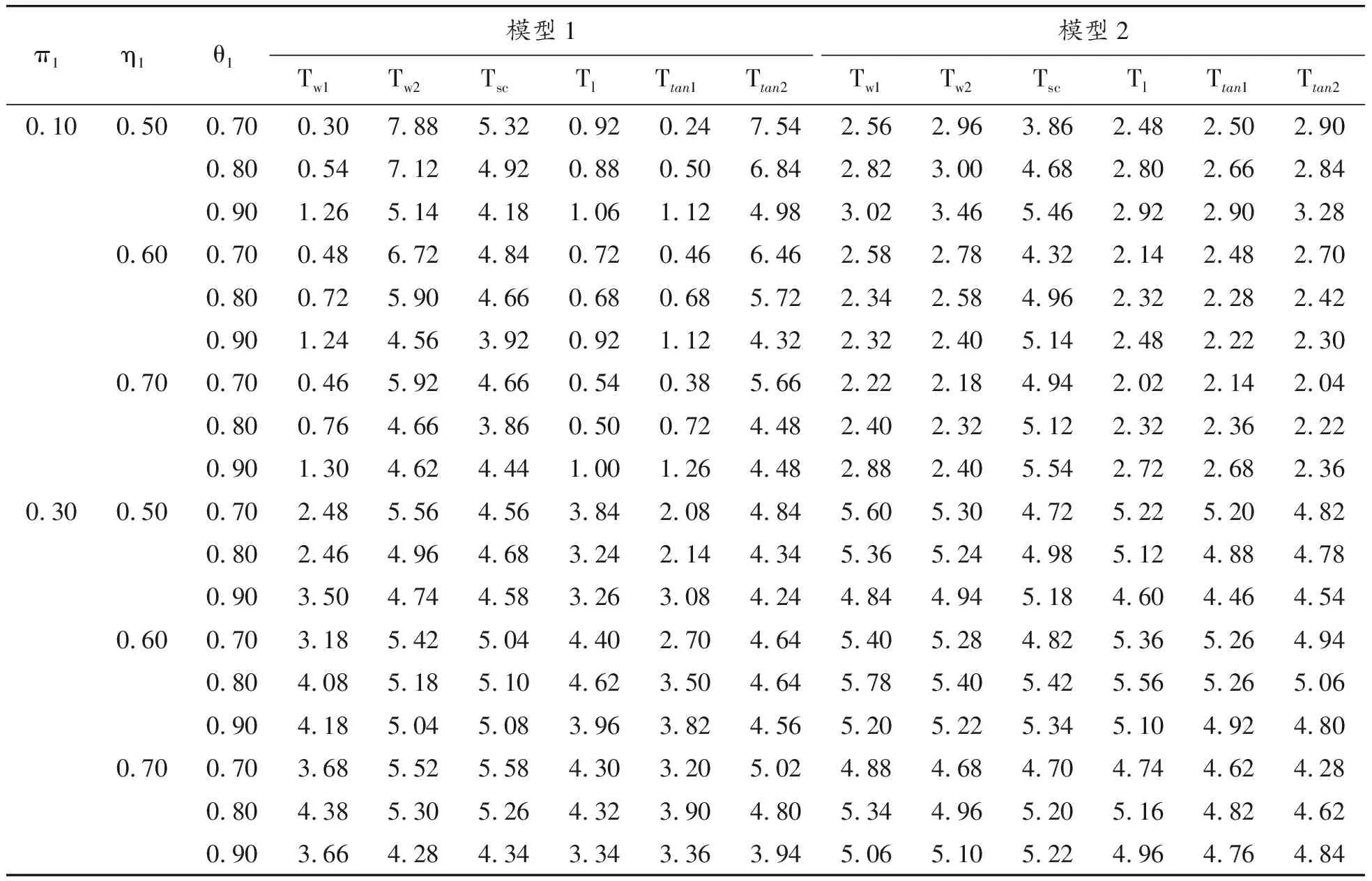
表6 中等样本(n1,n2,N1,N2)=(50,50,100,100)下犯第一类错误的概率(显著性水平α=0.05)

续表(表6)

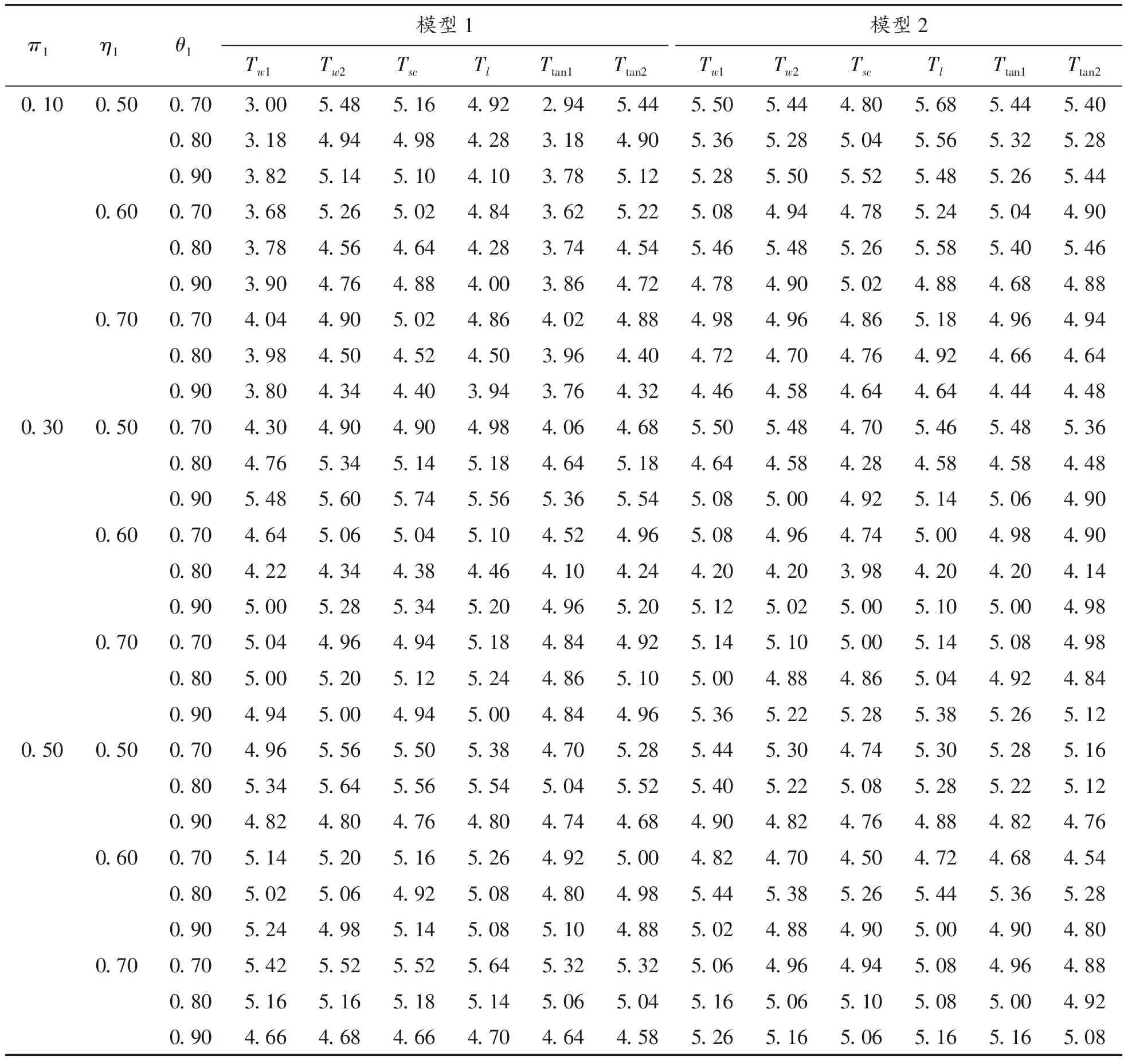
表7 大样本(n1,n2,N1,N2)=(200,200,500,500)下犯第一类错误的概率(α=0.05)

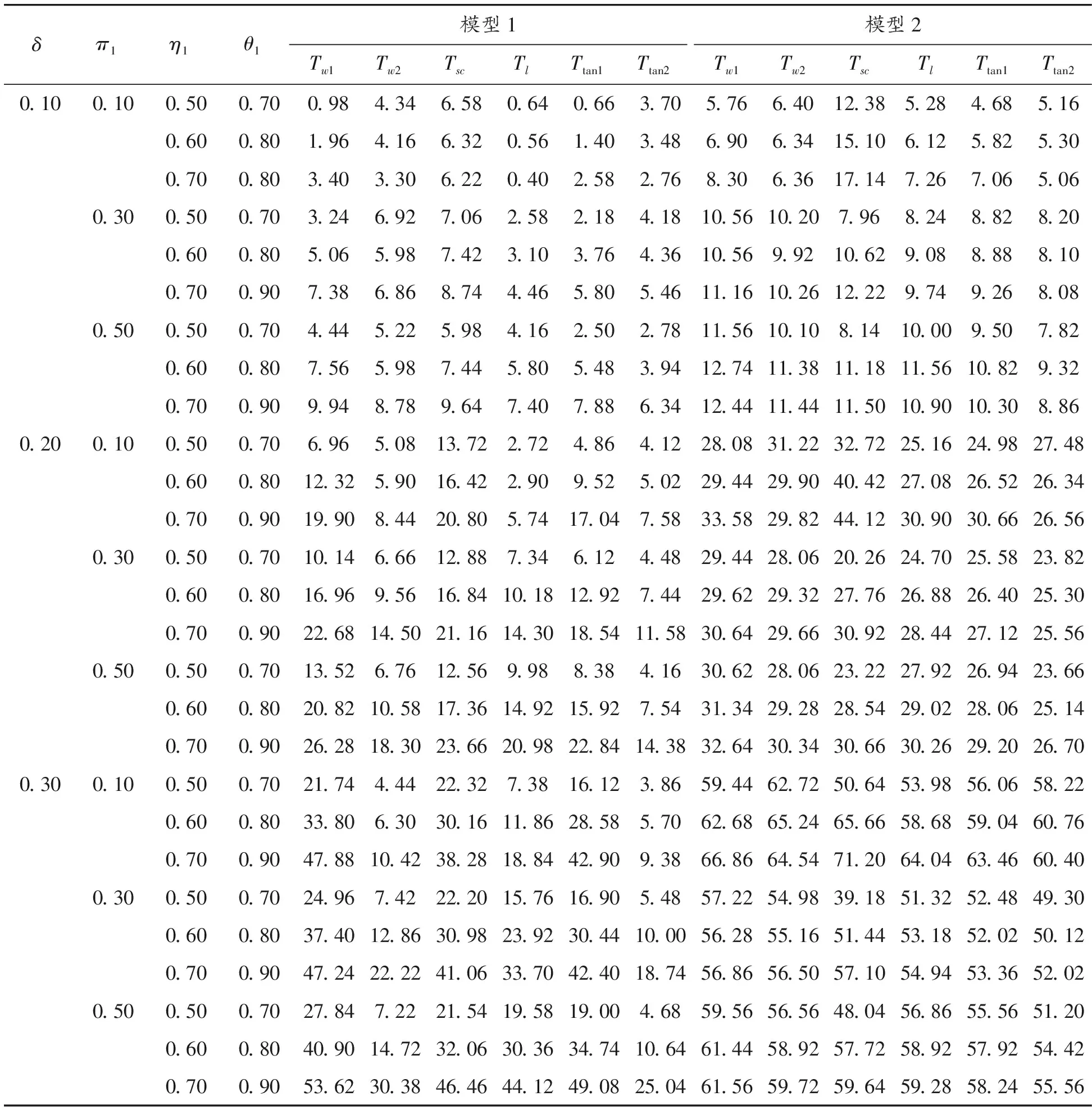
表8 小样本(n1,n2,N1,N2)=(20,20,30,30)下的经验功效(显著性水平α=0.05)

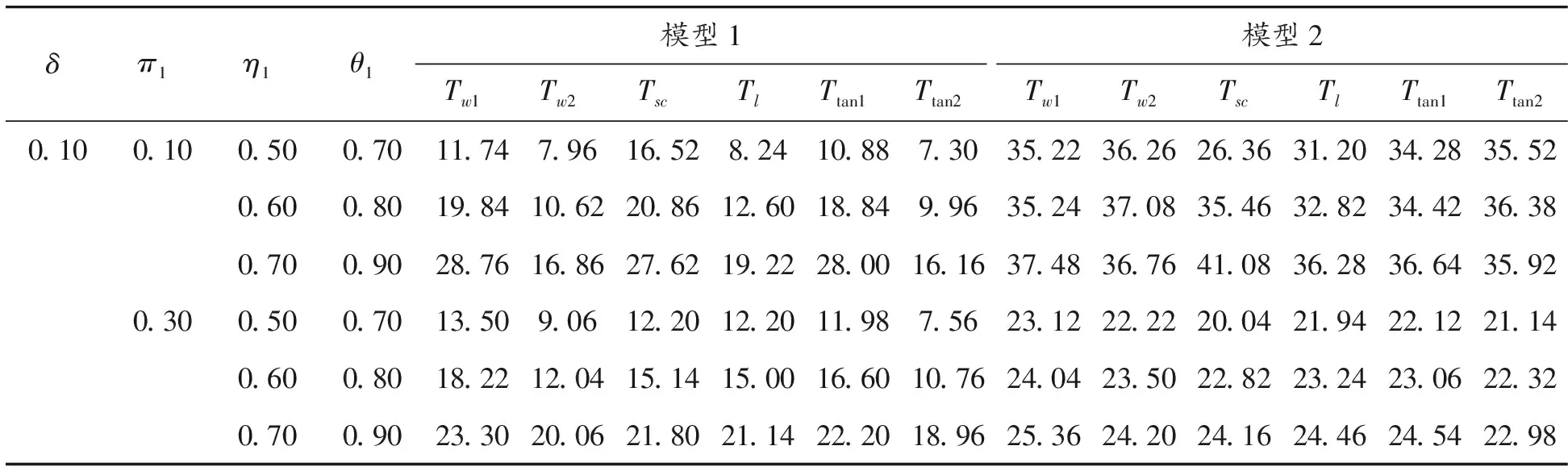
表9 中等样本(n1,n2,N1,N2)=(50,50,100,100)下的经验功效(显著性水平α=0.05)

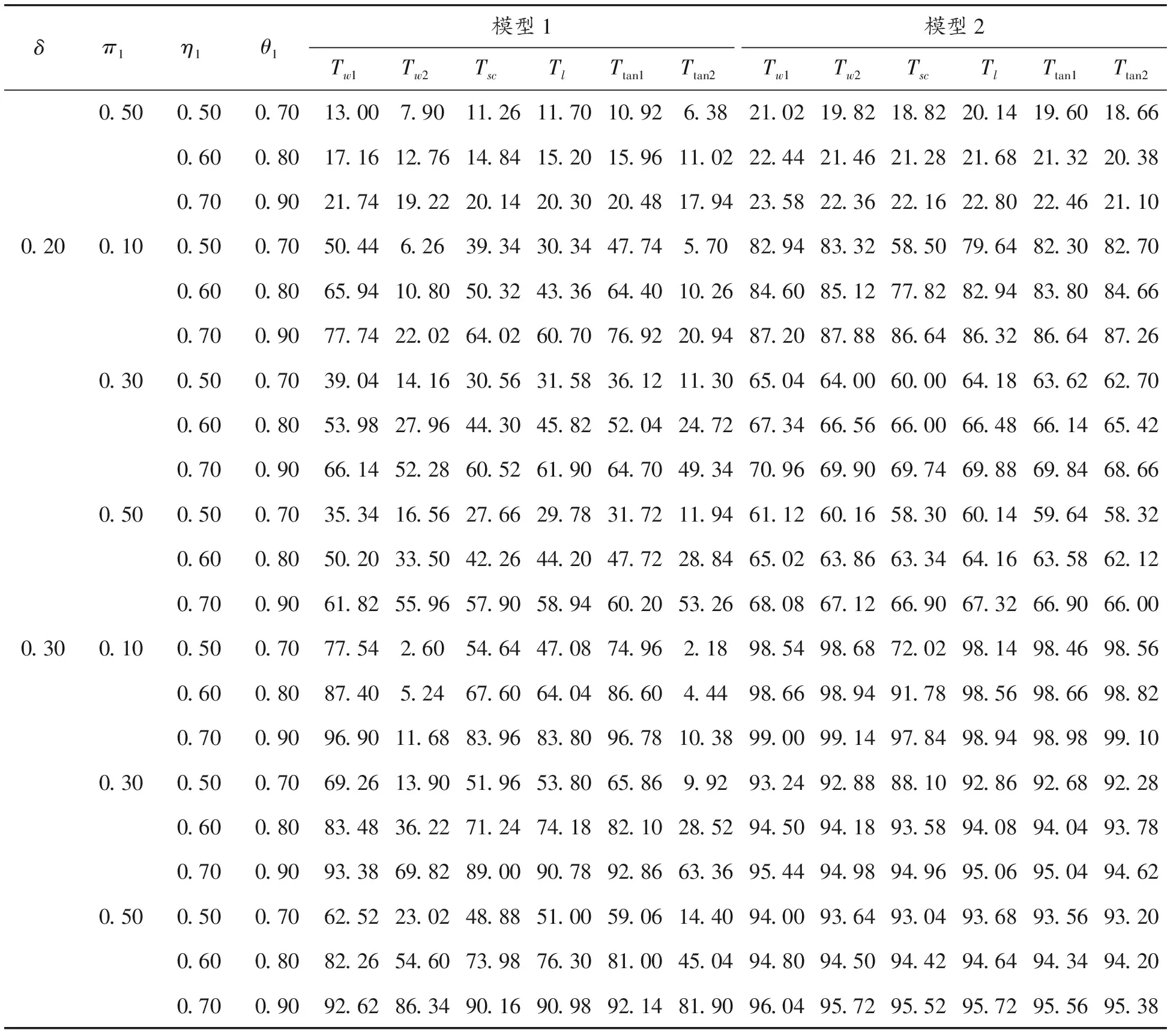
续表(表9)

通过模拟结果可以得到以下结论：① 对于2个模型，即使在极小样本(如(n1,n2,N1,N2)=(20,20,30,30))下，Score检验统计量(Tsc)犯第一类错误概率接近给定的显著性水平(α=0.05)，相应的功效也比较大，随着样本量的增大，犯第一类错误的概率越来越接近显著性水平0.05且功效越来越大；② 对于模型1，除了小样本情形，考虑原假设下方差的Wald检验统计量(Tw2)、Score检验(Tsc)以及反双曲正切变换统计量(Ttan2)都表现良好，它们犯第一类错误的概率都比较接近于给定的显著性水平0.05，且有较大的功效；③ 对于模型2，在中等样本和大样本且犯病率不是极小时，所有检验统计量犯第一类错误的概率都基本接近名义水平且具有较高的功效。综上所述，在模型1下，推荐使用Tw2、Tsc和Ttan1；在模型2下，当样本量极小时(如(n1,n2,N1,N2)=(20,20,30,30))，推荐使用Score统计量，在样本量不是极小时，所有统计量都可以推荐使用。

4 实例分析

为了验证本文提出方法的有效性，利用Nedelman[11]研究中的疟疾数据进行分析。考虑了未成年组(即9～18岁)的2个不同组的疟疾数据，数据结构见表10。

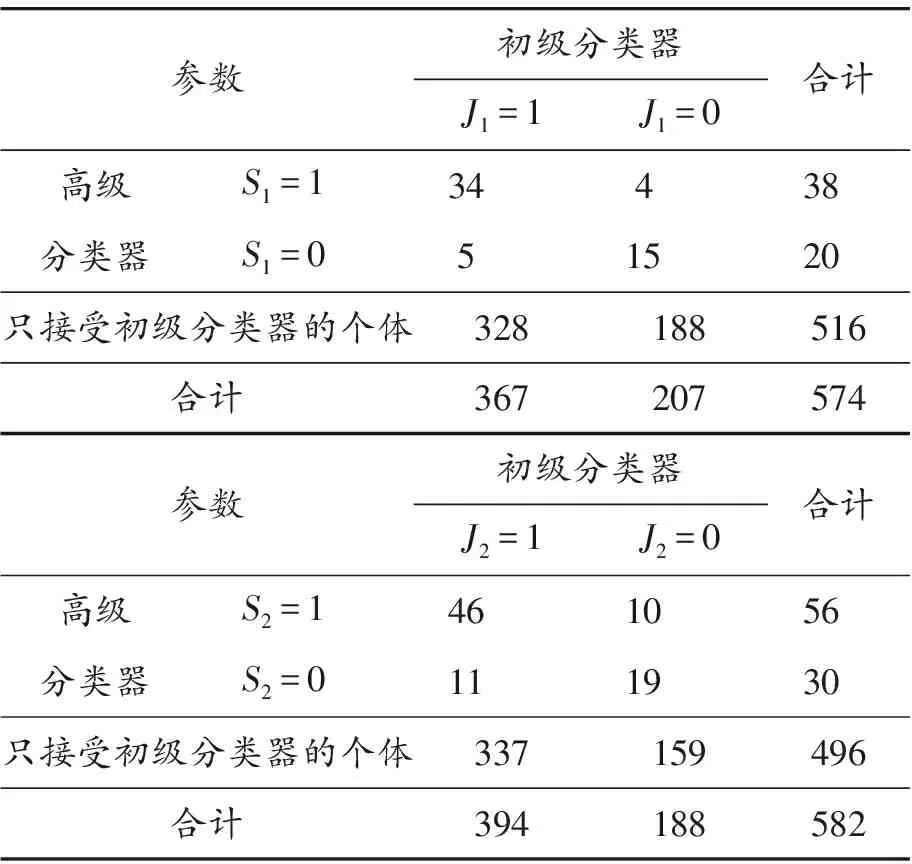
表10 实例数据

对于假设检验：H0:δ=0↔H1:δ≠0，在模型1下，基于本文考虑的检验统计量Tw1、Tw2、Tl、Tsc、Ttan1、Ttan2的检验p值分别为：0.113、0.130、0.129、0.184、0.115、0.132。由此，没有充分理由拒绝原假设，认为疟疾的患病率与不同的调查组无关。在模型2下，本文所提出的检验统计量的检验p值分别为：0.127、0.141、0.143、0.145、0.128、0.142，同样认为没有充分理由拒绝原假设，即认为疟疾的患病率与不同的调查组无关。

5 结束语

本文基于2个有误判分类器下的二重抽样数据对2组患病率进行了比较研究，分别考虑2个二重抽样模型的6种检验统计量，并通过不同样本量和不同参数设置考察了它们犯第一类错误的概率和检验功效。对于模型1，即使在极小样本下，Score检验以及反双曲正切统计量都表现良好，在样本量不太小时，似然比统计量也能很好地控制犯第一类错误的概率；对于模型2，本文所考虑的所有检验统计量(在中等样本和大样本下且犯病率不是极小时)都表现很好。在2个模型中，考虑初级分类器和高级分类器不存在假阳性，在实际的模型中该条件可能不存在，但如果2种分类器都存在假阳性分类时，本文考虑的模型是不可识别的。此时，可以考虑采用贝叶斯统计方法进行研究，这是一个将来值得研究的问题。