一种陶瓷材料断裂韧性压痕法计算公式

孙 亮，王家梁，石新正

一种陶瓷材料断裂韧性压痕法计算公式

孙 亮1，王家梁2，石新正1

(1. 陆军装甲兵学院 车辆工程系，北京 100072; 2. 武警工程大学 装备工程学院，陕西 西安 710086)

针对传统压痕断裂解析公式普遍存在测试精度较低、材料适用范围小的问题，基于陶瓷材料断裂韧性的维氏压入仿真分析结果，提出了一种新的陶瓷材料断裂韧性计算公式。对四种典型陶瓷材料试样的维氏压入实验结果表明，新公式的断裂韧性整体计算精度在±13.5%以内，与传统断裂韧性解析公式相比，在保持相当计算精度的同时，适用材料范围更加广泛。

陶瓷材料；断裂韧性；压痕法

0 引言

压痕断裂法是目前工程上测试陶瓷材料断裂韧性普遍采用的测试方法[1]，以Anstis等人[2]提出的经典公式IC=0.016(/)0.5(/1.5)为代表的压痕断裂解析公式多是基于Lawn等人[3]提出的LEM模型而建立。LEM模型给出了断裂韧性解析公式的基本形式IC=ξ(/)0.5(/1.5)，但无法通过力学推导得出解析式系数的具体数值。为获得解析公式系数ξ，后续研究者进行了大量工作，主要通过实验标定的方式确定该系数值[4,5]。课题组前期研究[6]发现，断裂韧性解析公式的测试精度较差且测试精度随陶瓷材料的压入比功[7,8]的变化而显著变化，并以材料压入比功为依据确定了几种常用断裂韧性解析公式的适用范围。可见，利用现有压痕断裂解析公式计算陶瓷材料断裂韧性，仍存在测试精度不高、实际适用范围小、公式不统一等问题。因此，本文以广泛的陶瓷材料压痕断裂仿真分析结果为基础，提出一种陶瓷材料断裂韧性计算公式，以解决断裂韧性解析公式应用不便的问题。

1 断裂韧性计算公式

由断裂韧性解析公式的基本形式IC= ξ(/)0.5(/1.5)可以看出，压痕法测试陶瓷材料断裂韧性的实验参数包括：材料弹性模量、接触硬度、最大压入载荷、压痕裂纹开裂半长，且公式主导项分别为/和/1.5。在前期研究工 作[6]中，课题组利用弹塑性有限元仿真方法及虚拟裂纹闭合技术针对广泛的陶瓷材料和不同的裂 纹开裂情况进行了数值仿真，其陶瓷材料弹性模量取值70GPa~600 GPa，屈服强度y涵盖 1400 MPa~30000 MPa，裂纹开裂半长与名义压痕对角线半长之比/包括1.05、1.25、1.5、2.25、3、4.5和6七种情况。本文进一步利用上述有限元仿真数据来分析材料性能参数/、压入实验参数/1.5与断裂韧性IC之间的数值关系。

图1 不同开裂情况下，106KIC·c1.5/P与E/H之间的相关关系

图1中(a)~(g)分别展示了不同裂纹开裂情况下，106IC·1.5/随/变化的相关关系。由图可知，除在/=1.05和1.25时存在少量偏离较大的数据点外，106IC·1.5/与/之间存在较明显的一一对应关系，对数据点进行回归分析即可得到106IC·1.5/与/间的数值关系。通过观察图1中(a)和(b)，可认为/分别取1.05、1.25且材料/值大于某一过渡值(/)'时，所建立公式的断裂韧性测试精度显著降低，即当/=1.05或1.25时，/≤(/)'的各数据点一致性较好，/>(/)'的各数据点一致性较差。为保证所建立公式的计算精度，以上述偏离点为依据对公式的应用范围进行限定。当/=1.05时，过渡值(/)'值为23.07，当/=1.25时，过渡值(/)'值为26.65，由此可通过线性拟合的方式得到一个可排除显著偏差点的简单计算方法(/)'=17.905(/)4.273。若实际(/)值小于(/)'值，则表明所建立断裂韧性计算公式适用，反之则不适用。排除偏差点后，对应不同/的106IC·1.5/E/关系如图2所示，

图2 106KIC·c1.5/P与E/H的相关关系及其拟合曲线

对其进行拟合，则上述关系可以确定为

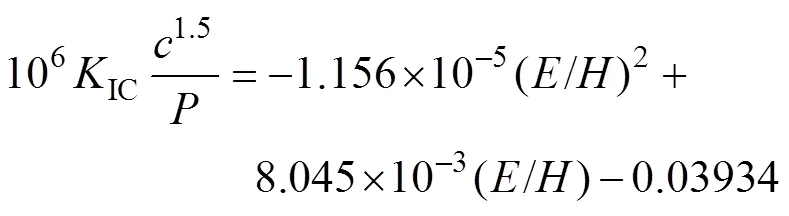
经变换，即得到新的压痕法断裂韧性计算 公式

其中，IC的单位为MPa∙m1/2，的单位为N，的单位为m。其适用范围为：1.5≤/≤6且9.3≤/≤32.4及1.05≤/≤1.25且9.3≤/≤17.905(/)-4.273。

2 实验验证

实验选用氮化硅Si3N4、氧化锆增韧氧化铝ZTA、氧化铝Al2O3、熔融硅SiO2等四种典型陶瓷材料为对象，四种材料试样的断裂韧性IC及弹性模量的参考值均取自参考文献[9]，其值见表1。所制备试样均符合国际标准ISO14705-2016[10]要求。

利用宏观Vickers压入仪[11]对四种材料试样进行压入测试，Si3N4、ZTA、Al2O3三种材料的压入测试载荷为100N，SiO2的压入测试载荷为2N。四种材料的维氏压痕形貌如图3所示。对每种材料的压入测试均重复10次，取10次实验平均值作为最终测试结果。为便于比较，应用本文建立的公式(2)以及三种代表性的传统断裂韧性解析公式-Evans公式[12]、Lawn公式[3]和Anstis公式[2]计算上述材料的断裂韧性IC值，其计算结果见表2。新公式与三种典型公式的断裂韧性计算误差列于表3。

由表3可知，新公式对Si3N4、ZTA、Al2O3等三种材料的断裂韧性计算精度与传统解析公式相当，而对SiO2的计算精度则远好于三种传统解析公式。这说明本文建立的新公式与传统解析公式相比，在保持相当测试精度的同时，具有更大的材料适用范围，验证了所建立公式的有效性。

表1 四种陶瓷材料的断裂韧性IC及弹性模量参考值

Tab.1 Reference values of KIC and E of the four tested samples

图3 四种陶瓷材料的维氏压痕形貌

表2 新公式及三种典型公式的断裂韧性计算结果(IC/MPa·m1/2)

Tab.2 Tested fracture toughness of the proposed and three representative formulas (KIC/MPa·m1/2)

表3 新公式及三种典型公式的断裂韧性计算误差

Tab.3 Test errors of the proposed and three representative formulas

3 结论

(1) 基于陶瓷材料断裂韧性有限元仿真分析结果，提出了一种新的陶瓷材料断裂韧性压痕法计算公式，与几种代表性的传统解析公式相比，新公式在未改变实验设备和测试参数的情况下，整体测试精度提高、材料适用范围更加广泛。

(2) 对四种典型陶瓷材料进行压入实验，结果表明：新公式对四种材料的测试误差范围小于±13.5%，且对于SiO2试样的测试误差远小于三种传统解析公式。上述结果证明了新公式在陶瓷断裂韧性测试上的有效性。

[1] 陈立佳, 王毅, 郝善朋, 等. 溶液等离子喷涂氧化锆涂层力学性能的研究[J]. 人工晶体学报, 2017, 46(7): 176-180. CHEN L J, WANG Y, HAO S M, et al. Journal of Synthetic Crystals, 2017, 46(7): 176-180.

[2] ANSTIS G R, CHANTIKUL P, LAWN B R, et al. A critical evaluation of indentation techniques for measuring fracture toughness: I, direct crack measurements [J]. Journal of the American Ceramic Society, 1981, 64(9): 533-538.

[3] LAWN B R, EVANS A G, MARSHALL D B. Elastic/plastic indentation damage in ceramics: the median/radial crack system [J]. Journal of the American Ceramic Society, 1980, 63(9-10): 574-581.

[4] NIIHARA K, MORENA R. HASSELMAN D P H. Evaluation of KIC of brittle solids by the indentation method with low crack-to-indent ratios [J]. Journal of Materials Science Letters, 1982, 1(1): 13-16.

[5] MIYOSHI T, SAGAWA N, SASA T. Study of evaluation for fracture toughness of structural ceramics [J]. Journal of Japanese Society for Mechanical A, 1985, 51: 2489-2497.

[6] 王家梁, 马德军, 白盟亮, 等. 传统压痕法识别陶瓷材料断裂韧性的有效性研究[J]. 材料工程, 2015, 43(12): 81-88. WANG J L, MA D J, BAI M L, et al. Journal of Materials Engineering, 2015, 43(12): 81-88.

[7] CHENG Y T, CHENG C M. Relationships between hardness, elastic modulus, and the work of indentation [J]. Applied Physics Letters, 1998, 73(5): 614-616.

[8] MA D J, ONG C W, ZHANG T H. An improved energy method for determining Young's modulus by instrumented indentation using a Berkovich tip [J]. Journal of Materials Research, 2008, 23(8): 2106-2115.

[9] MA D J, WANG J L, SUN L. Methodology for measuring fracture toughness of ceramic materials by instrumented indentation test with Vickers indenter [J]. Journal of the American Ceramic Society, 2017, 100(5): 2296-2308.

[10] ISO 14705-2016. Fine ceramics (advanced ceramics, advanced technical ceramics)-Test method for hardness of monolithic ceramics at room temperature[S].

[11] 马德军, 宋仲康, 郭俊宏, 等. 一种高精度压入仪及金刚石压头压入试样深度的计算方法[P]. 中国专利: CN102288500A, 2011-12-21.

[12] EVANS A G, CHARLES E A. Fracture toughness determination by indentation [J]. Journal of the American Ceramic Society, 1976, 59(7-8): 371-376.

A New Formula for Calculating Fracture Toughness of Ceramics by Indentation

SUN Liang1, WANG Jialiang2, SHI Xinzheng1

(1. Department of Vehicle Engineering, Academy of Army Armored Forces, Beijing 100072, China; 2. College of Equipment Engineering, Engineering University of Chinese Armed Police Force, Xi’an 710086, Shaanxi, China)

Traditional analytical formulas for indentation fracture toughness of ceramics are commonly troubled with low accuracy and narrow application range. Hence, a modified formula for indentation fracture toughness is proposed based on the simulation data of Vickers indentation on ceramic materials. Results of Vickers indentation tests on four representative ceramic samples indicated that, the proposed formula could apply to broader range of ceramic materials with an acceptable accuracy (within ±13.5%) than traditional analytic fracture toughness formulas.

ceramic materials; fracture toughness; indentation method

date: 2019‒03‒25.

date:2019‒05‒20.

孙亮(1990-)，男，博士。

TQ174.75

A

1000-2278(2019)04-0530-05

10.13957/j.cnki.tcxb.2019.04.020

2019‒03‒25。

2019‒05‒20。

Correspondent author:SUN Liang(1990-), male, Ph.D.,E-mail:tproud@163.com