基于极小碰集求解算法的测试向量集约简
2019-11-15欧阳丹彤陈晓艳邓召勇张立明
欧阳丹彤 陈晓艳 叶 靖 邓召勇 张立明
1(吉林大学计算机科学与技术学院 长春 130012) 2(计算机体系结构国家重点实验室(中国科学院计算技术研究所) 北京 100190) 3(符号计算与知识工程教育部重点实验室(吉林大学) 长春 130012) 4(中国科学院计算技术研究所 北京 100190)
随着信息产品需求的增长,集成电路市场也在其带领下迅速发展,电路的复杂度不断增加,使得电路的测试成本不断提高.为了解决这一问题,人们在设计阶段就开始考虑可测试性问题,以保证自动测试向量生成(automatic test pattern generation, ATPG)过程得以有效进行.ATPG的任务是针对特定的故障模型确定1个高质量测试向量集(test pattern set, TPS),使得设计的故障覆盖率达到期望值[1].在工业界,以Synopsys,Mentor Graphic,Cadence这3家公司为代表的芯片设计公司都提供了商用的ATPG工具.由Synopsys公司开发的TetraMAX ATPG 2018是现阶段工业界功能最强和最容易使用的ATPG工具,针对不同的电路设计,TMAX 2018可以在很短的时间内生成具有高故障覆盖率的TPS.本文中将TetraMAX ATPG 2018简记为TMAX 2018.
TPS的规模对电路的测试成本,如测试时间、测试功耗以及被测电路的寿命等问题有较大影响[2].为了缩短测试时间、降低测试成本,国内外学者在TPS优化、TPS压缩等领域进行了大量研究.TPS优化问题根据不同的优化目标可以大致分为2类:1)以故障覆盖率与故障隔离率为可测试性指标,以测试代价最小为目标对TPS进行优化,在优化的过程中,可测试性指标要求故障覆盖率与故障隔离率均不低于某个值,是兼顾测试成本、检测与诊断效果的优化方式[3-4].2)TPS优化问题的目的是对TPS进一步约简,求出其没有冗余的最小TPS,使其向量个数最少,同时尽可能保证故障覆盖率保持不变[5-9].在约简的过程中,并没有考虑TPS的诊断效果与测试所需的代价.优化之后的TPS将提供给自动测试仪(automatic test equipment, ATE)的测试程序使用.TPS压缩问题是指,在ATE测试的过程中,测试数据被存储在ATE的存储器中,由于ATE有限的存储资源和测试带宽往往难以满足片上系统高速测试的实际需求,通常要对测试数据进行压缩,减少测试过程中需要存储的数据空间,把数据转换成比原格式更紧凑的形式.测试数据压缩作用于待测电路对应的TPS,并对其进行压缩存储[10-11].
在TPS优化问题研究领域,国内外许多学者对保证TPS覆盖率不变的同时减少TPS数目的TPS约简问题进行了研究.俞龙江等人[5]提出基于蚁群算法的TPS约简算法,对最初的蚁群算法模型进行修正,设置参数较少,多次运行可以获得相同解,具有较强的鲁棒性,但是不能保证最终解中没有冗余的测试向量;乔家庆等人[6]提出利用遗传排序算法对TPS中的测试向量顺序进行优化,并采用行列消去法作为适应度评估算法,有效地减少了测试向量的数目,优于传统的遗传算法,但是遗传算法本身收敛速度慢、寻优效率低,容易陷入局部最优的算法仍然不可避免;侯艳丽等人[7]将粒子群算法应用于TPS约简问题,该算法重新定义粒子的位置和速度,利用具有全局优化能力的混沌算法将初始化粒子群,并且粒子针对故障编码,使得初始个体本身就是1个完备TPS,取得了较好的效果,但使用的参数往往依据经验设置,以最优解的适应性没有变化作为结束条件,在实际的应用中有一定的局限性;曹义亲等人[8]提出基于粗糙集的TPS优化算法中,利用粗糙集的知识约简理论构造电路对应知识系统,生成区分函数,对该函数进行求解得到最小TPS,该算法可以有效平衡约简效果与约简所用时间,但是不能保证约简后TPS的覆盖率与原TPS相同;王宏力等人[9]提出的基于粒子群的多目标TPS优化算法(以下简记为PSO-Td),以最大故障覆盖率和最少测试向量数目为优化目标,对TPS进行约简,取得了较好的约简效果.
以上TPS约简算法在尽可能保证约简后的TPS故障覆盖率保持不变的情况下,最大程度减少TPS中的测试向量数目,随机算法得到的TPS约简结果具有一定的随机性.在对以上工作的深入研究基础上,本文提出基于极小碰集求解算法[12-13]的极小完全测试集求解算法(minimal complete test pattern set reduction, MCTPSR).
该算法只需要针对TPS建立测试向量与需要检测的故障列表之间的对应关系,生成对应的向量覆盖集合簇,将TPS的约简问题转化为极小碰集的计算问题,即可使复杂的约简问题通过简单的模型得到解决.该算法的主要优点有5方面:
1) 可以得到所有的极小解,是完备性算法,同时保证所有解中都没有冗余的测试向量;
2) 可以很好地适应TPS约简问题,且其计算效率比较高,约简产生的开销远远小于因冗余测试所产生的开销;
3) 模型简单,仅需要结合测试向量与故障之间的对应关系重新建模即可求解,且求解过程不需要其他参数和多次迭代;
4) 具有选择的多样性,对于1个TPS,往往可以得到多个极小解,可以根据实际的测试开销选择合适的解;
5) TPS的约简不会降低故障覆盖率,同时由MCTPSR算法产生的所有解都可以保证有效性.
1 预备知识
本节介绍TPS约简问题、基于模型诊断和碰集的相关概念,以及MHS-DMECV算法中使用的相关概念与定义,并通过实例进行说明.
1.1 TPS约简
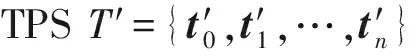
例1.设某电路中的故障集F={f0,f1,f2,f3},TPST={t0,t1,t2},其中t0对应的故障集为F0={f0,f1},t1对应的故障集为F1={f2},t2对应的故障集为F2={f2,f3}.显然在T中,t1是1个冗余的测试向量,因此会被删除,最终保留测试向量t1和t3,T′={t1,t3},使F1∪F3=F,TPST被约简为T′.
1.2 碰 集
定义1[14].1个系统可定义为1个三元组(SD,COMPS,OBS),其中:
1)SD为系统描述,是一阶谓词公式集;
2)COMPS是系统组成部件的集合,是1个有限常量集;
3)OBS为观测集,是一阶谓词公式的有限集.
定义2[14].冲突集CS是1个部件集{c1,c2,…,cn}⊆COMPS,当且仅当SD∪OBS∪{AB(c1),AB(c2),…,AB(cn)}是不一致的.其中AB为一元谓词,表示“abnormal”.AB(c)为真,当且仅当c异常,且c∈COMPS.
定义3[14].碰集.设CS={Si|i=1,2,…,n}是集合簇,称HS为CS的1个碰集,如果HS满足:
1)HS⊆∪S;
2) 对于任意1个S∈CS都有HS∩S≠∅.
集合簇CS的1个碰集是极小碰集(minimal hitting set, MHS)当且仅当它的任意真子集都不是CS的碰集.
例2.对于集合簇CS={{1,2},{2,3},{2,4}},根据碰集的定义,通过计算得到CS的碰集HS有{2},{1,2},{2,3},{2,4},{1,2,3},{1,2,4},{2,3,4},{1,2,3,4}.其中,集合簇CS的MHS为{2}和{1,3,4}.
1.3 MHS-DMECV算法
本节介绍极小碰集算法MHS-DMECV中的相关定义与概念,并给出实例进行说明.
定义4[12].容量.若集合簇CS中包含元素的个数为n,则称n为集合簇CS的容量,记为CAP(CS)=n.
设U是集合簇CS中所有元素的并集构成的集合,即U=∪Si={e1,e2,…,em},用Car(U)表示集合U的势,即集合U中元素的个数.
定义5[12].频数.若e∈S,则称集合S含有元素e,记Freq(CS,e)表示集合簇CS中含有元素e的元素的个数,称为元素e在集合簇CS中的频数.
定义6[12].元素覆盖值.若元素e在集合簇CS的某个元素Si(i=1,2,…,n)中出现,且在当前状态下Si中没有其他元素出现,则称元素e覆盖Si;若对于集合簇CS中的所有元素,元素e能覆盖的元素个数为C,则称C为元素e的元素覆盖值,记为Cover(e).显然0≤Cover(e)≤Freq(CS,e).
例3.对于集合簇CS={{1,3},{2,4},{1,2,3}},CS的容量Cap(CS)=3,CS中所有元素的并集U={1,2,3,4},集合U的势为Car(U)=4,元素1在CS中的频数Freq(CS,1)=2,因为元素1在CS的元素中出现了2次.对于集合簇CS,若首先选择元素1,由于它能覆盖集合{1,2}和{1,2,3},所以元素1的元素覆盖值Cover(1)=2,若接着选择元素2,此时集合{1,2}和{1,2,3}已被覆盖,所以它能覆盖的集合只有{2,4},因此Cover(2)=1,接下来若选择元素3或4,此时所有集合都被覆盖,所以Cover(3)和Cover(4)的值在该时刻都为0,因此不需要选择元素3或4,只需要元素1和2就可以完成对集合簇CS中所有集合的覆盖.不难看出CS的1个碰集是{1,2},由于其非空真子集{1},{2}都不能覆盖CS中的所有元素,因此{1,2}为CS的1个极小碰集.
2 MHS-DMECV算法
本节通过伪代码描述MHS-DMECV算法,并通过实例介绍其流程.
算法1.MHS-DMECV算法[12].
输入:待处理序列Seq、(与Seq对应的)Head邻接链表数组和元素覆盖值Cover数组、碰集保存容器HittingSet、集合簇CS的元素覆盖标志数组SetFlag、已覆盖数AlreadyCover;
输出:集合簇CS对应的所有MHS.
① 初始化:
AlreadyCover=0,HittingSet=∅,
SetFlag=[0×CAP(CS)],
根据CS初始化Seq序列、Head数组、Cover数组;
② Begin
③ While (Seq≠[])
④e←Seq第1项;
⑤ Ife是最后1项and
Cover(e)+AlreadyCover=Cap(CS)
⑥container←{e}∪HittingSet;
⑦ EndIf
⑧ Ifcontainer是极小碰集
⑨SetMHS=SetMHS∪container;
⑩ Return;
Seq表示对U中元素的Cover值从大到小排列得到的序列;Head是用来存储U中每个元素对应于CS中的集合索引的邻接链表;update(),update(Seq′)表示更新相关变量信息;un_update()表示撤销对相关参数的更新;create(Seq)表示构建新的Seq′和与其对应的Head′,Cover′.
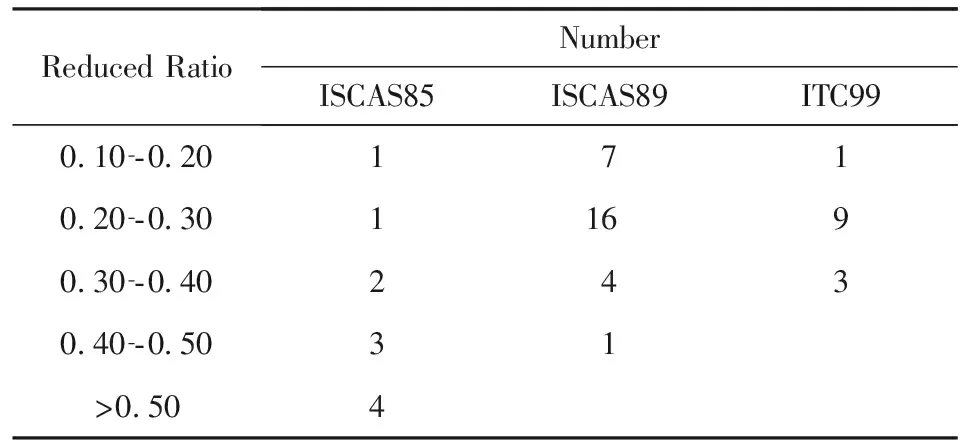
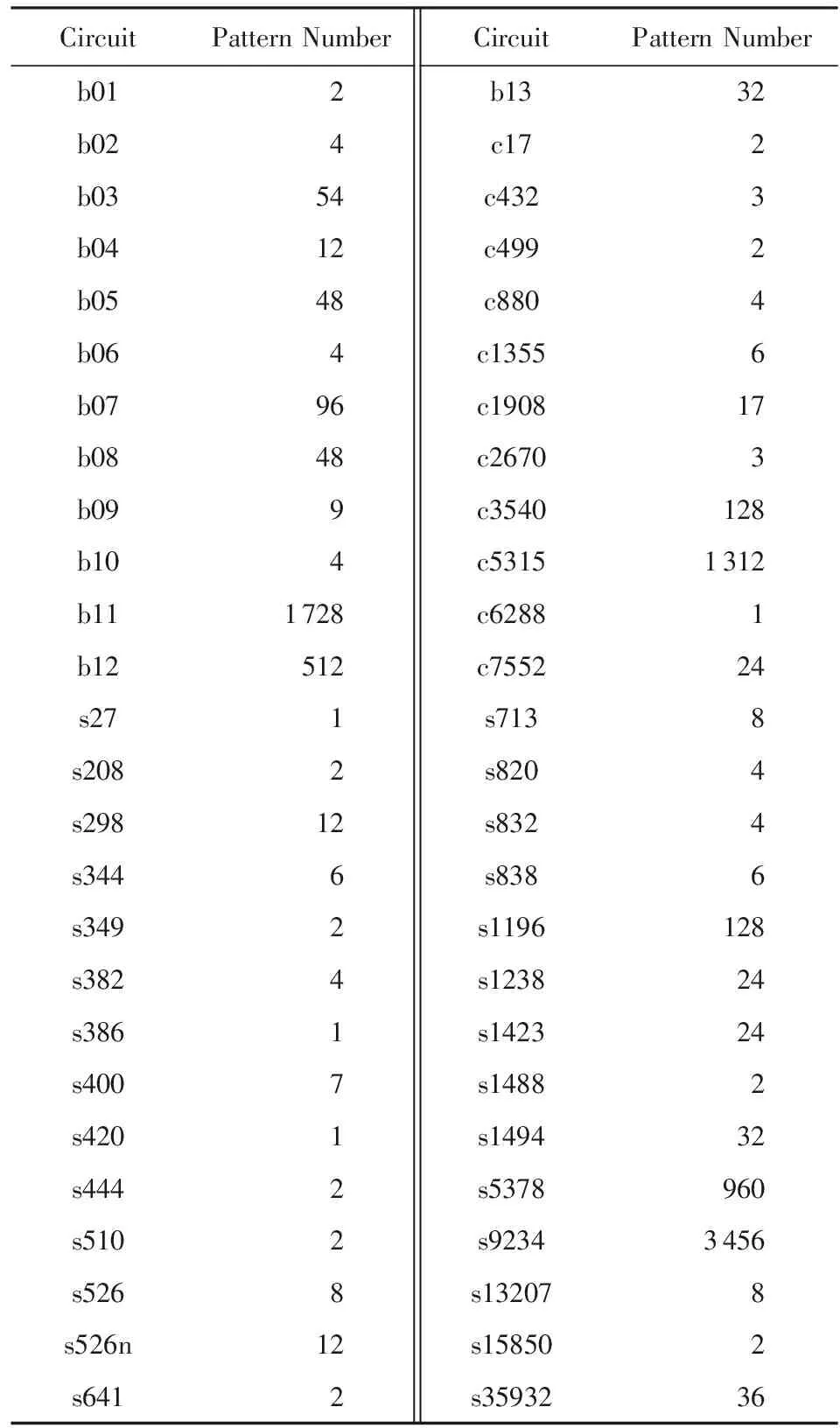
例4.对于集合簇CS={{1,3},{2,3}},初始时,Cover(1)=1,Cover(2)=1,Cover(3)=2.根据元素的Cover值,得到的Seq序列为[3,1,2],其对应的Head如图1所示,此时还没有元素被选中,因此此时没有集合被覆盖,AlreadyCover=0,SetFlag=[0,0].首先处理Seq序列中的第1项“3”,更新相关参数值,AlreadyCover=2,SetFlag=[1,1],Seq′=[],CanCover=0,AlreadyCover+CanCover=CAP(CS),因此得到CS的1个碰集{3},将其加入HittingSet,根据极小碰集的定义判断出{3}是集合簇CS的1个极小碰集,将其加入SetMHS;接着处理元素1,此时新的待处理序列Seq″=[2],对应的Head如图2所示,此时AlreadyCover=1,因为集合{1,3}已经被Seq序列中的第2项“1”覆盖,而集合{2,3}没有被Seq序列中的第2项“1”覆盖,因此元素覆盖标志数组SetFlag=[1,0],可以覆盖的元素数CanCover=1,由于AlreadyCover+CanCover=CAP(CS),可以得到CS的1个碰集{1,2},通过判断得出它是1个极小碰集,将其加入SetMHS;然后处理Seq序列中的第3项“2”,此时Seq中没有其他元素,AlreadyCover=1,且AlreadyCover+Cover(2) 算法的完备性已在文献[12]中进行证明. Fig. 1 The adjacency list Head corresponding to pending sequence Seq′图1 待处理序列Seq′对应的邻接链表Head Fig. 2 The adjacency list Head corresponding topending sequence Seq″图2 待处理序列Seq″对应的邻接链表Head 本节对TPS约简问题进行建模,介绍其与极小碰集求解问题中相关联的概念,并通过伪代码描述基于MHS-DMECV的TPS约简算法MCTPSR. 本节介绍TPS约简问题的相关概念与定义,并通过实例进行说明,同时对TPS约简问题进行建模,将其转化为适合极小碰集求解算法处理的模型. 定义7.故障序列.电路中可能发生的所有故障组成的拥有确定顺序的集合,记为F={f0,f1,…,fn},F的容量为n. 在文献[6]中描述了完全测试集的概念,下面我们给出标准定义. 称CTPST是极小完全测试集(minimal complete test pattern set, MCTPS).当且仅当T的任意1个真子集都不是CTPS. 定义9.覆盖值.如果测试向量ti(ti∈T)可以检测到电路中的故障fj(fj∈F),则称该测试向量ti覆盖了故障fj,(ti,fj)的覆盖值为1,记为Cij=1,否则Cij=0. 定义10.故障覆盖集.若t∈T可以检测到电路中的故障{fi,fj,…,fk}(0≤i,j,k≤n),则t对应的故障覆盖集为{fi,fj,…,fk}(0≤i,j,k≤n),记为Ft={fi,fj,…,fk}(0≤i,j,k≤n). 定义11.向量-故障矩阵.设T={t0,t1…,tm}是电路的1个TPS,F={f0,f1,…,fn}是电路中的故障序列,由T,F中的元素ti与fj的覆盖关系Cij组成的矩阵,称为该电路的向量-故障矩阵,记为PFM. 例5.设TPST={t0,t1,t2,t3},故障集合F={f0,f1,f2,f3,f4},其中,t0的故障覆盖集为F0={f0,f3,f4},因此可以得到覆盖值C00=1,C01=0,C02=0,C03=1,C04=1,同理可以得到T中其他测试向量与故障fj∈F的覆盖值,这些覆盖值构成PFM,如表1所示.其中,PFM(0,0)=0表示测试向量t0不能覆盖到故障f0,PFM(1,3)=1表示测试向量t1可以覆盖到故障f3.从表1可以看出,T={t0,t1,t2,t3}是1个TPS,但由于其子集{t0,t1,t2}依然可以覆盖F中的全部故障,它显然不是1个MCTPS.实际上,由F0={f0,f3,f4},F2={f1,f2,f3},可以得出F0∪F2=F,因此{t0,t2}构成1个MCTPS,同理,由于F0∪F1∪F3=F,且{t0,t1,t3}的任意1个真子集都不是TPS,因此{t0,t1,t3}也是1个MCTPS. Table 1 An Example of PFM表1 PFM实例 定义12.向量覆盖集.若fj∈F,则称集合Tj是故障fj的向量覆盖集,如果对于所有的ti∈Tj,都有Cij=1.记为PCS(fj)={ti|Cij=1}. 例6.如表1所示,在故障f0对应的1列数据中,C0j=1的测试向量为t0,0≤j≤3,因此PCS(f0)={0}.同理可得,故障f1对应的PCS(f1)={1,2},故障f2对应的PCS(f2)={2,3},故障f3对应的PCS(f3)={0,2,3},故障f3对应的PCS(f4)={1,2}. 本节给出基于极小碰集算法MHS-DMECV的MCTPS求解算法MCTPSR的伪代码并对其进行说明. 算法2.MCTPSR算法. 输入:电路网表文件; 输出:电路对应的MCTPS. ①mkdir(); ②source_gen(); ③ If需要添加扫描链 ④run_dc(); ⑤ EndIf ⑥T,F=run_tmax(); ⑦pats=pat_split(T); ⑧ Fori,pat∈pats ⑨F′=run_tmax_single(pats); ⑩v=vector_gen(F′,F,T); 行①mkdir()用于生成电路目录及子目录,行②中source_gen()用于生成电路所需的脚本文件;如果当前电路是时序逻辑电路文件,则需要添加扫描链以生成综合网表文件与协议文件(其中规定了扫描链与时钟等约束信息)(行③~⑤);行⑥~⑦首先通过运行TMAX 2018生成TPST以及故障序列F,并且将T中的测试向量分离为单独的测试向量pat;之后,每一个测试向量pat作为外部测试向量读入TMAX 2018可以得到单个测试向量pat对应的故障列表F′并与F,T一起作为vector_gen()的输入,从而得到PFM中的1行向量v,同时更新PFM(行⑧~);行表示根据PFM生成向量覆盖集PCS组成的集合PCSs,作为极小碰集求解算法的输入;行调用MHS-DMECV算法,产生对应的极小碰集,即电路的MCTPSresults;行~中get_coverage()实际上是结果检验的过程,对results中的所有结果,形成新的TPS,载入TMAX 2018检测TPS的故障覆盖率是否保持不变. 本节对MCTPSR算法的性能进行实验分析,在实验对比部分,选取TMAX 2018产生的TPS作为比较对象.同时在初始潜在解的覆盖率最高的情况下对PSO-Td算法进行了重现,并与其实验结果进行对比.实验环境为:Ubuntu 14.04,CPU Intel Core i7-4700HQ 2.40 GHz,8 GB RAM,python.使用Design Compiler完成添加扫描链的工作,TMAX 2018生成TPS以及新的MCTPS的覆盖率检验. 利用TMAX 2018产生测试集时,所使用的故障模型是固定型故障(stuck-at fault, SAF),SAF的优点有: 1) 易于生成故障列表,且故障总数随着电路中的逻辑门的个数线性增长,故障列表的规模可以控制; 2) 可以覆盖所有SAF的测试集,对于芯片中的其他类型的故障也有很高的覆盖率; 3) 很多故障模型都可以用不同的SAF的组合表示. SAF针对芯片中的单个故障,而实际芯片一般包含多个故障,已有实验表明,可以覆盖所有单故障的测试集在检测多故障时同样拥有很高的覆盖率[15].因此,本文实验选择SAF作为ATPG过程的故障模型. 本文使用了国际测试界ATPG研发经常使用的基准电路ISCAS85[16]、全扫描版本的ISCAS89[17]电路和ITC99[18]电路,其电路规模如表2所示. 表3~5分别描述了对ISCAS85,ISCAS89,ITC99中的部分电路对应的TPS的约简效果.表格中的列1(Circuit)是各电路的名字;列2(TMAX)表示电路对应的TMAX 2018生成的TPS中的测试向量数量;列3(MCTPSR)表示通过MCTPSR算法得到的MCTPS中极小TPS中包含的测试向量的数量;列4(Reduce)表示MCTPSR算法约简掉的测试向量的个数;列5(Reduced Ratio)表示约简的部分在TPS中所占的比例. Table 2 Basic Information of Test Circuits表2 测试电路基本信息 Table 3 Comparison in TPS of ISCAS85表3 ISCAS85电路TPS对比 Table 4 Comparison in TPS of ISCAS89表4 ISCAS89电路TPS对比 Table 5 Comparison in TPS of ITC99表5 ITC99电路TPS对比 由表3~5可以看出,针对规模不同、类型不同(ISCAS85是组合逻辑电路,ISCAS89和ITC99是时序逻辑电路)的电路对应的TPS,MCTPSR算法都起到了很好的约简效果.对所有电路的TPS约简比例都在10%以上,针对电路c3540和c5315甚至产生了高于50%的约简效果. 表6中对本文提出的MCTPSR算法与PSO-Td算法结果进行对比,表6中Circuit列表示电路名称,MCTPSR列表示本文所提算法的约简结果中的最小解,PSO-Td列表示PSO-Td中提出算法的约简结果(由于PSO-Td算法的实验结果具有随机性,实验中取近5次实验结果中的最小值进行比较).PSO-Td算法应用于规模较大的电路时,不能在可接受的范围内求出解,表6中用空白表示.可以看出MCTPSR算法明显优于PSO-Td算法. Table 6 Compare Reduced Results Produced by MCTPSRwith Results of PSO-Td Table 7 Circuit Number with Different Reduced Ratio Range Table 8 Number of MCTPS Generated by MCTPSR表8 MCTPSR算法的MCTPS个数 表8中给出由MCTPSR算法得出的MCTPS的个数.可以看出,对于不同的电路,往往有多个MCTPS,MCTPSR算法可以得到所有MCTPS,这为实际的芯片测试过程提供了很强的可选择性,可以通过计算不同测试集的测试开销,选择成本合适的测试集,可以很大程度地降低芯片的测试成本. 实验结果表明:MCTPSR算法对TMAX 2018产生的TPS有很好的约简效果,而且可以得到不止1个MCTPS,为芯片测试提供了多种选择.在实际应用中,可以极大地降低芯片测试成本,加快芯片的生产过程. 本文通过对MCTPS约简问题进行重新建模,将复杂的约简问题转化为极小碰集的求解问题,结合基于动态极大元素覆盖值求取所有极小碰集的MHS-DMECV算法提出MCTPSR算法,对商用工具TMAX 2018产生的TPS进行约简,缩减了工具生成的TPS规模,计算效率较高,约简产生的开销比较小;其次,该算法的模型简单,只需要测试向量与故障的对应关系矩阵就可以进行求解,且过程中不需要其他参数,不需要进行多次迭代就可以得到解;该算法对于1个TPS,往往可以得到不止1个极小解,可以根据实际的测试开销选择合适的解;同时,TPS的约简不会降低故障覆盖率.MCTPSR可以在保证故障覆盖率的前提下提供更小的TPS,对降低芯片生产过程中的测试开销有着重要的现实意义.

3 MCTPSR算法
3.1 问题建模


3.2 算法描述
4 实 验
4.1 故障模型
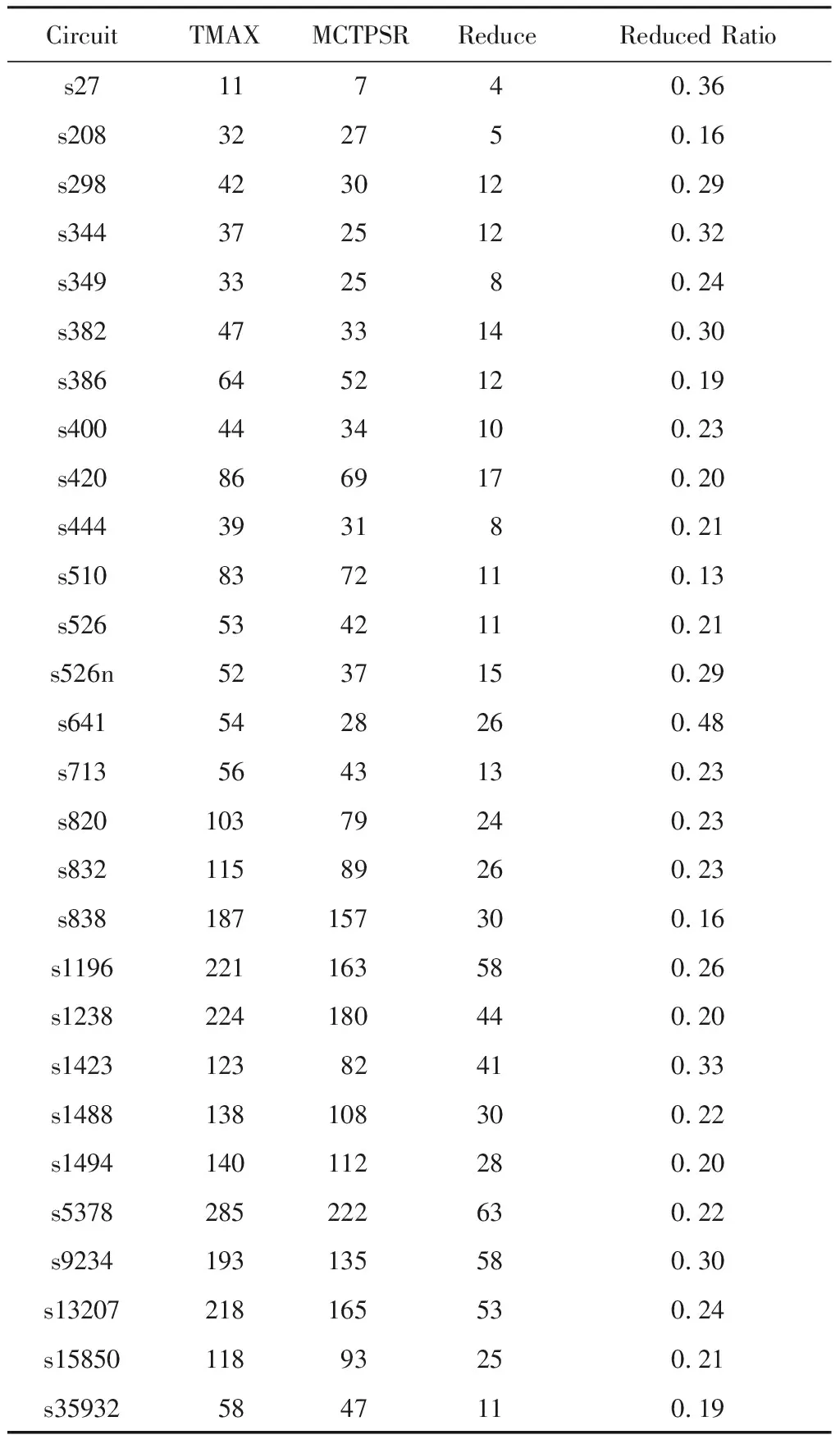
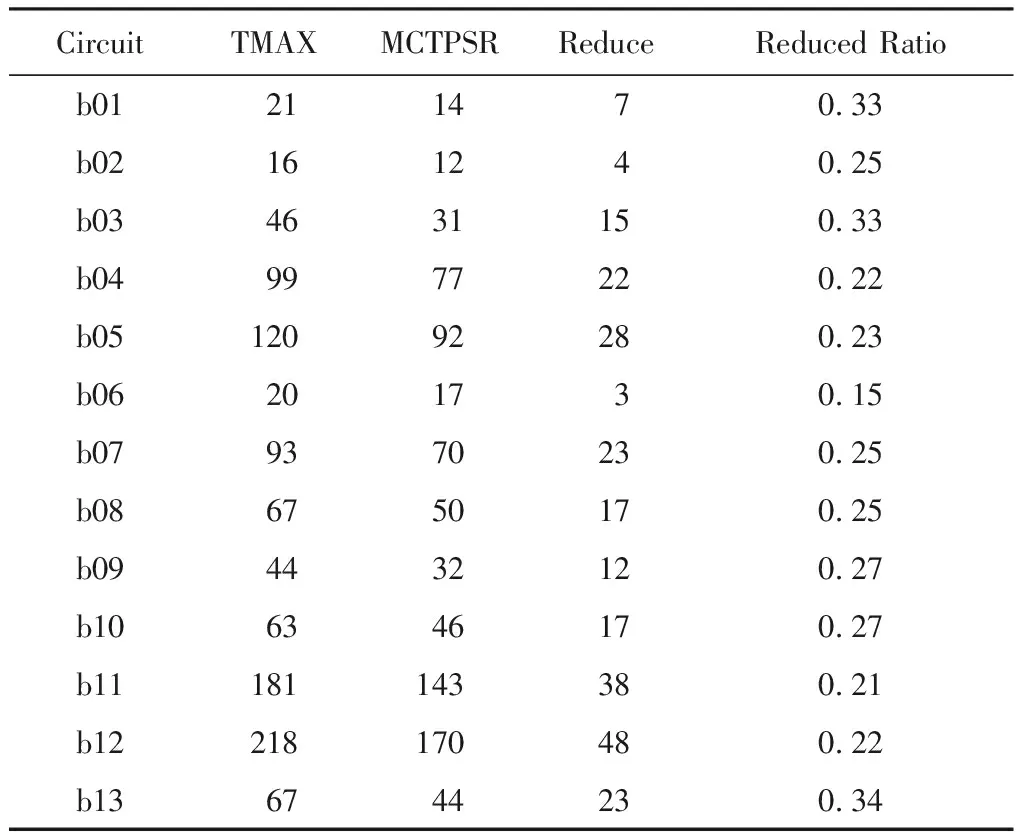
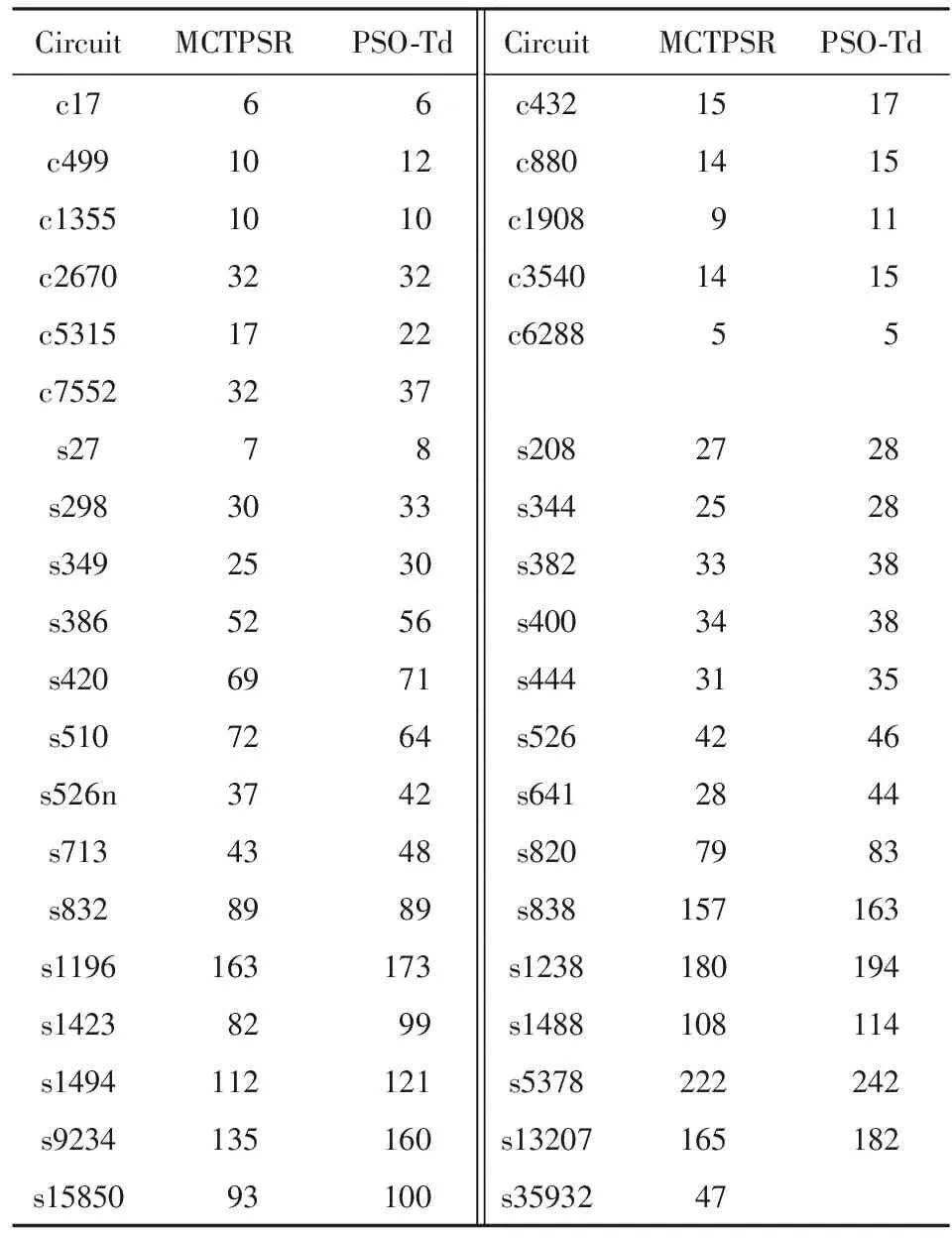
4.2 实验结果



5 总 结
