基于相似度量的自适应三支垃圾邮件过滤器
2019-11-15张清华王国胤
谢 秦 张清华 王国胤
(计算智能重庆市重点实验室(重庆邮电大学) 重庆 400065)
互联网时代使人类获取信息的方式更加便捷多样,但也给人类带来了诸如垃圾邮件等有害信息.对于某些人群来说,若邮件被错分则会带来非常大的损失,如风险投资者因一封投资分析报告邮件被错分到了垃圾邮件类,则其投资计划将会因为信息获取不及时而遭受巨大损失.因而提高过滤器的分类准确率及召回率等指标对于垃圾邮件过滤来说至关重要.在业界,垃圾邮件过滤通常被视为一个二分类问题.目前,机器学习领域中的大量二分类模型都可被用来处理垃圾邮件过滤问题,如k近邻分析法[1]、朴素贝叶斯(Naive Bayes, NB)分类器[2]、基于集成学习的分类器[3]等.然而,由于二分类模型武断地把邮件归类为垃圾邮件类或合法邮件类,因此会导致决策过程中产生较大的错分代价进而导致分类精度较低.此外,由于二分类模型在分类时过于直接,因此常常无法确定最优阈值.
三支决策模型实质上是在二分类模型的基础上加入了延迟决策域.换言之,三支决策模型的主要优点在于其允许延迟决策的可能性.如果做出延迟决策的代价不高,则三支决策模型是一个有效的选择.此外,从人类认知的角度出发,三支决策模型将不能确定类别的邮件放到延迟决策域,用户可以依据实际需求查看延迟决策域里的邮件,可达到灵活选择有价值的邮件的目的.目前,三支决策研究领域已有不少的成果,如文献[4]将不能合理地判别是垃圾邮件或合法邮件的邮件称为灰色邮件,并提出了4种原型检测方法.此外,根据粗糙集[5-6],文献[7-9]提出了决策理论粗糙集模型,并受到了广大学者的关注,如文献[10]基于决策粗糙集提出了一种解决修饰和不修饰情感词语情况下的否定句情感分类模型.进一步地,为给决策粗糙集中的3个域赋予一定的语义,文献[11-12]提出了基于决策理论粗糙集的三支决策(three-way decision with decision-theoretic rough sets, 3WD-DTRSs)模型.3WD-DTRSs模型是一种依据贝叶斯决策规则,以最小化期望代价为目标来确定一对阈值并将待判对象划分为3个域(接受域、拒绝域及延迟决策域)的三支决策模型.3WD-DTRSs模型的研究成果同样丰富,如文献[13]提出了一种基于犹豫模糊决策理论粗糙集的风险决策方法.文献[14]给出了一种用于在给定接受域对象数量的情况下,建立具有给定属性值的三支决策模型.值得提出的是,在3WD-DTRSs模型研究中,阈值的计算一直是一个研究热点,研究者已给出一些计算方法[15-19],如文献[20]提出了一种利用相对值确定3WD-DTRSs模型的损失函数的方法.垃圾邮件过滤过程从代价的角度可以解释为,将一个实为垃圾邮件的邮件判断为垃圾邮件的代价小于将其判断为延迟决策的代价,而将其判断为延迟决策的代价又小于将其判断为合法邮件的代价.同理,将一个实为合法邮件的邮件判断为合法邮件的代价小于将其判断为延迟决策的代价,而将其判断为延迟决策的代价又小于将其判断为垃圾邮件的代价.而3WD-DTRSs模型中的代价逻辑正好与之契合.因此,文献[21]将3WD-DTRSs模型用于解决垃圾邮件分类问题,并从代价敏感等角度阐明了模型的优势.
然而,在3WD-DTRSs模型研究领域,存在这样一种情况,当2个等价类的粗糙隶属度相同时,2个等价类必定会划分到同一个区域.从模型原理的角度出发,这种现象存在的原因为在3WD-DTRSs模型中,粗糙隶属函数反映的是等价类与目标集的交叉程度,而由专家给定的损失函数是将所有对象视作等价的,换言之,对于每一个等价类,只要等价类中的对象与目标集合的交叉度相同,则粗糙隶属度相同,且损失函数都是相同的.然而,当二者所对应的各条件属性值相差比较大的时候,二者在直观上不应该属于同一区域.从条件属性值的角度出发,等价类与目标集合的相似度越大,该等价类在同等条件下更应该被划分到正域,换言之,等价类之间是存在差异的.若仍然按照3WD-DTRSs模型的原理,忽略等价类之间的差异性,则在贝叶斯决策准则下推导出来的阈值并不能使得所有等价类达到全局的最小划分代价,进而导致模型精度表现不够理想.然而,目前少有研究在给定或者构造损失函数时考虑由于等价类之间存在差异而带来的影响.因此,现有的3WD-DTRSs模型在模型性能上还存在一定的研究价值.已有工作[22]考虑等价类之间存在差异性等因素,基于效用理论给出了一种改进的基于决策粗糙集的三支决策模型.然而该模型在基于效用函数构造风险度量函数时,需要主观给定风险偏好参数,则该模型的泛化能力还有待提高.此外,相似度量是一种度量2个对象之间相似度的工具,且相似度量的方法相当丰富[23-24],如相关系数、欧氏距离及集合相似度等.在垃圾邮件过滤领域,文献[25]提出了一种用于垃圾邮件图像聚类分析的非负稀疏相似性度量方法. 此外,刘伍颖等人[26]给出了一种基于结构化集成学习的垃圾邮件过滤器.因此,为了解决上述各问题,从集合相似度量角度出发,考虑等价类之间存在差异性等因素,提出了一种基于相似度量的自适应三支垃圾邮件分类器(similarity measure based adaptive three-way spam filter, SBA-3WD-SF).
首先根据集合方差给出了一种计算属性重要度的方法,并基于此提出了一种计算条件属性权重的方法;其次,根据集合相似度给出了一种度量等价类中条件属性值与目标集合中相应属性值的贴近度的方法;然后,进一步给出一种自动确定综合评价函数的方法以度量风险,并根据贝叶斯准则,给出了一种计算自适应阈值的方法.实验结果表明,所提的SBA-3WD-SF在准确率及召回率方面优于二元NB分类器及3WD-DTRSs分类器.换言之,SBA-3WD-SF是合理有效的.
1 基础知识
1.1 基本定义
定义1.不可分辨关系.[2]给定一个信息系统S=(U,C∪D,V,f),对于属性子集∀B(B⊆C∪D),论域U上的一个不可分辨关系IND(B)可定义为
IND(B)={(x,y)|(x,y)∈U2,
∀b∈B∧(b(x)=b(y))}.
(1)
定义2.近似集.[2]给定一个信息系统S=(U,C∪D,V,f),对于∀X(X⊆U)及不可分辨关系IND(B),集合X的上下近似集可分别定义为

(2)
其中,
UIND(B)={X|X⊆U∧∀x,y∈X∧
∀b∈B∧(b(x)=b(y))}
表示由等价关系IND(B)在论域U上诱导的划分.
从而,非空有限论域可被划分为3个互不相交的区域,即正域(POS(X))、负域(NEG(X))及边界域(BND(X)):
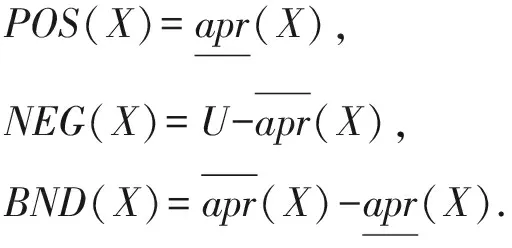
(3)
定义3.粗糙隶属函数.[27]给定一个信息系统S=(U,C∪D,V,f),则对于∀X(X⊆U)及不可分辨关系IND(B),关于目标集合X的粗糙隶属函数可定义为
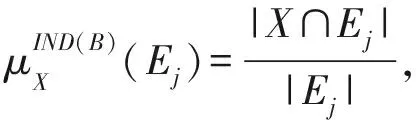
(4)
1.2 相关研究
为了突出贡献,本节将分别简要介绍一个二分类及一个三分类垃圾邮件分类器的代表模型,即二元NB分类器与3WD-DTRSs分类器.
1.2.1 二元NB分类器
文献[28]提出了贝叶斯理论,文献[29]提出了特征条件独立性假设,文献[30]将二者结合并提出了NB垃圾邮件过滤器.二元NB分类器是垃圾邮件过滤的一种最常用的二分类方法. 假设每一个待判的邮件对象x均可用一个m维的特征向量V(x)=(v1(x),v2(x),…,vm(x))表示,X表示垃圾邮件类,X表示合法邮件类. 有别于定义3中的条件概率Pr(X|Ej),可根据等价类与目标集的交并而获得,而NB分类器主要是通过将面向单一对象的条件概率Pr(X|V(x))转换为易于求解的后验条件概率Pr(V(x)|X)的方式来解决难以直接求解Pr(X|V(x))的问题.根据贝叶斯定理及全概率公式,给定一个邮件V(x)=(v1(x),v2(x),…,vm(x)),其属于垃圾邮件类X的后验概率(一种判别函数)为

(5)
其中,
Pr(V(x))=Pr(X)Pr(V(x)|X)+
Pr(X)Pr(V(x)|X),
Pr(X)为X的先验概率,Pr(V(x)|X)表示给定邮件V(x)时,V(x)∈X的似然函数.事实上,似然函数Pr(V(x)|X)是一个联合条件概率Pr(v1(x),v2(x),…,vm(x)|X),然而,当m比较大时,在实践中很难分析v1(x),v2(x),…,vm(x)之间的相互作用.因此,条件独立性假设被应用于贝叶斯分类器,即假设当给定垃圾邮件类X时,每一个特征vi(x)(i=1,2,…,m)与其余特征都是条件独立的,在表达式上体现为
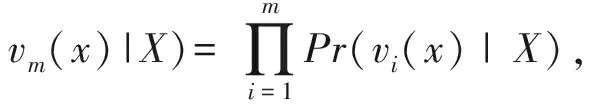
(6)
其中,Pr(vi(x)|X)能很容易地从数据中估计得到.从而式(5)可以表示为
(7)
同理,后验概率Pr(X|V(x))可以表示为
Pr(X|V(x))=
(8)
因此,概率Pr(V(x))可以被消除,即有:
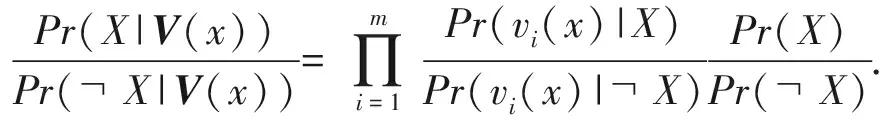
(9)
1.2.2 3WD-DTRSs模型
作为三分类模型的一个代表模型,本节将简要介绍3WD-DTRSs模型[11].首先,决策理论粗糙集模型[8]包含2个状态T={X,X}及3个动作A={aP,aB,aN}.根据3个动作,由专家经验给出的损失函数如表1所示:
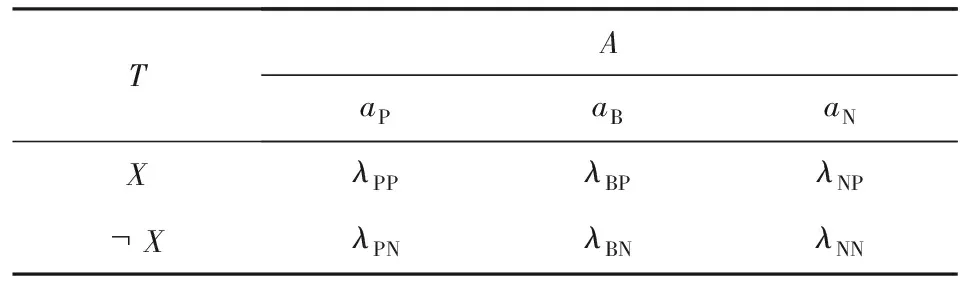
Table 1 Loss Function Given by Expertise表1 由专家经验给定的损失函数
由表1得知:在垃圾邮件过滤这个背景下,状态X及X分别表示垃圾邮件类及合法邮件类.λPP,λBP,λNP分别表示一个本应该属于垃圾邮件类的对象分别采取动作aP,aB,aN而产生的损失.同理λPN,λBN,λNN分别表示一个本应该属于合法邮件类的对象分别采取动作aP,aB,aN而产生的损失.对于任意待判邮件x(x∈Ej),采取不同动作而产生的期望损失可表示为
R(aP|Ej)=λPPPr(X|Ej)+λPNPr(X|Ej),
R(aB|Ej)=λBPPr(X|Ej)+λBNPr(X|Ej),
R(aN|Ej)=λNPPr(X|Ej)+λNNPr(X|Ej).
(10)
根据贝叶斯决策过程中最小化损失原则,则决策规则为
(P)如果R(aP|Ej)≤R(aB|Ej)且R(aP|Ej)≤R(aN|Ej),则Ej⊆POS(X);
(B)如果R(aB|Ej)≤R(aP|Ej)且R(aB|Ej)≤R(aN|Ej),则Ej⊆BND(X);
(N)如果R(aN|Ej)≤R(aP|Ej)且R(aN|Ej)≤R(aB|Ej),则Ej⊆NEG(X).
由于Pr(X|Ej)+Pr(X|Ej)=1,则上述规则只与损失函数及判别函数Pr(X|Ej)有关,一个合理假设为λPP<λBP<λNP,λNN<λBN<λPN.且简记为
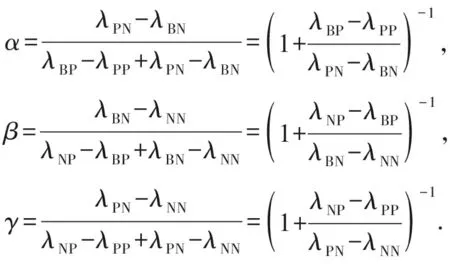
(11)
则决策规则(P)(B)(N)可等价地表示为
(P)如果Pr(X|Ej)≥α,则Ej⊆POS(X);
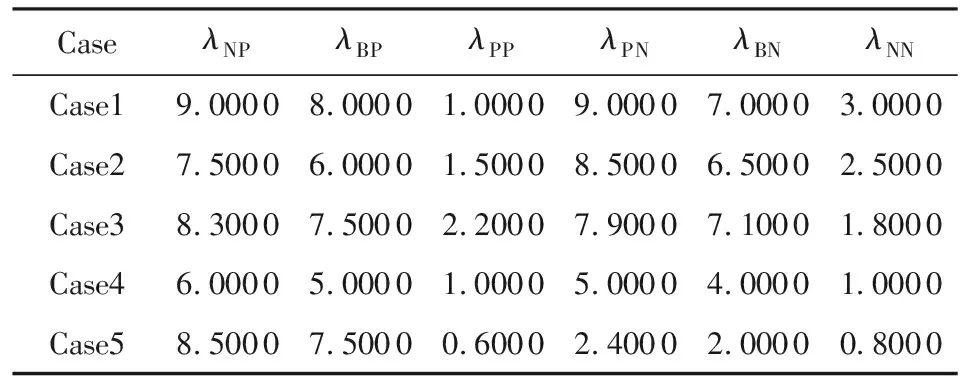
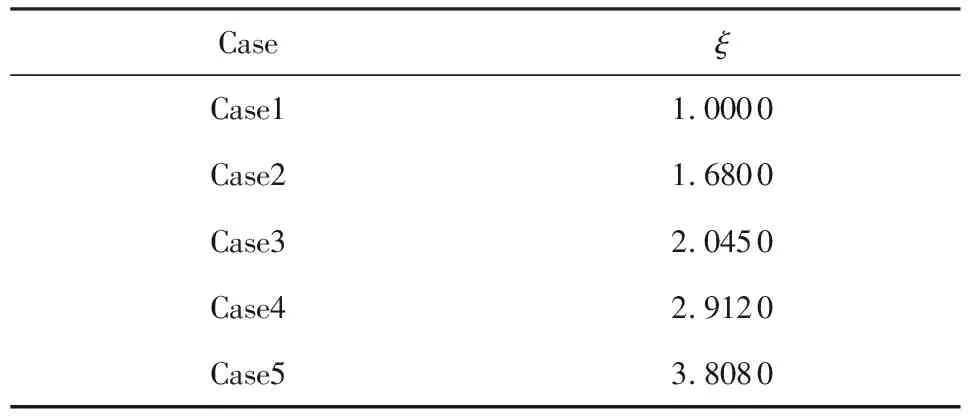
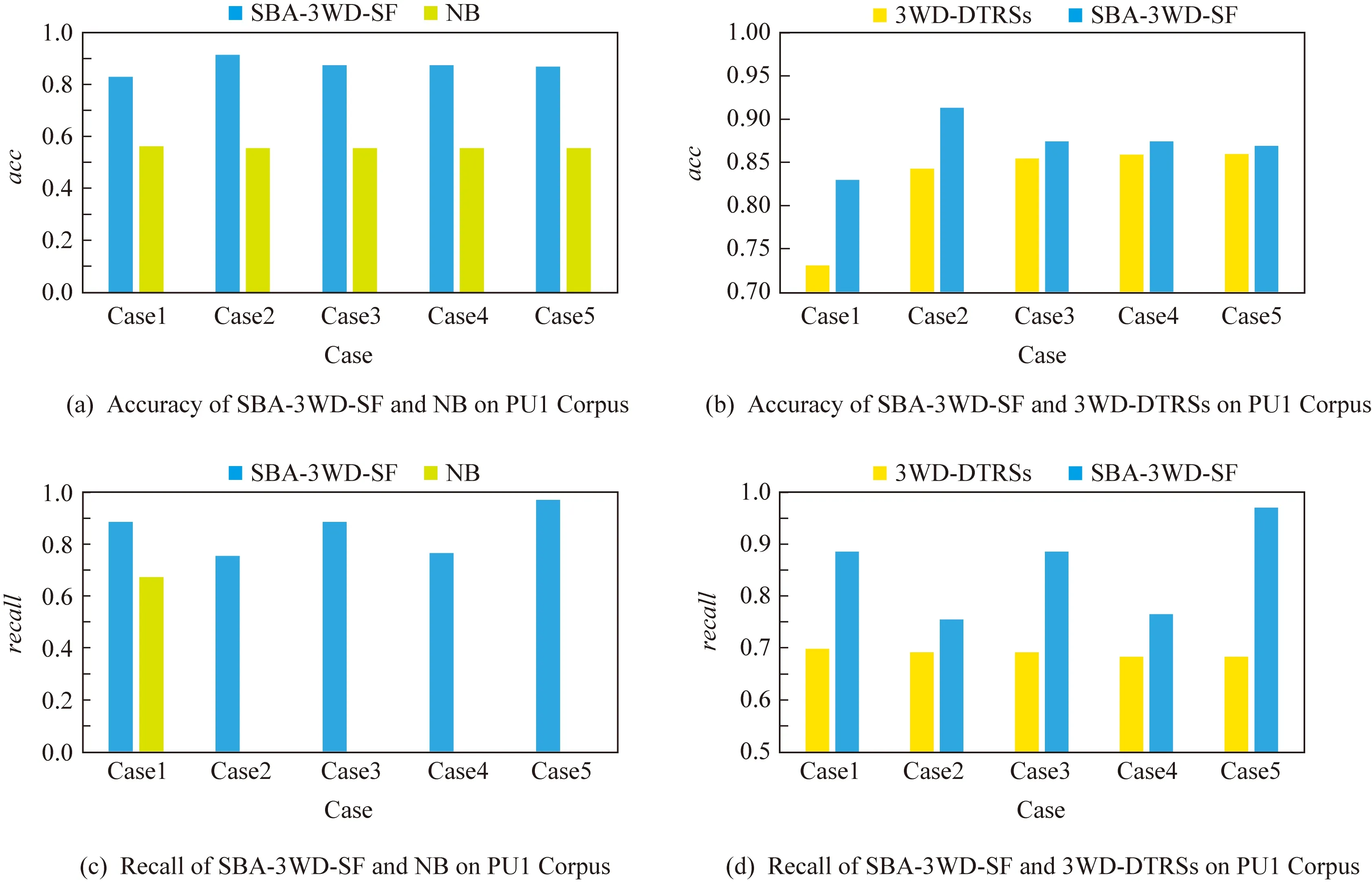
(B)如果β (N)如果Pr(X|Ej)≤β,则Ej⊆NEG(X). 综上所述,二分类模型及三支决策模型的差异如图1所示.对于二分类模型,如果对象的判别函数Pr(X|x)≥ξ,则该对象被接受;反之,该对象被拒绝.对于三支决策模型,如果对象的判别函数Pr(X|x)≥α,则该对象被接受;如果该对象的判别函数Pr(X|x)≤β,则该对象被拒绝;如果该对象的判别函数α>Pr(X|x)>β,则该对象被归入延迟决策域. Fig. 1 Binary and three-way classification图1 二支及三支分类 当前,作为一种简单而有效的方法,距离度量被广泛地应用于各个领域.其中,欧氏距离是距离度量中的一种简单且易于理解的方法.在统计领域,欧氏距离[31]常被用来度量2个向量的距离. 2个向量Y=(y1,y2,…,ym)和Z=(z1,z2,…,zm)之间的欧氏距离定义为 (12) 其中,欧氏距离d(Y,Z)的取值范围为[0,+). 在一个信息系统S=(U,C∪D,V,f)中,对于任意对象x(x∈U),各条件属性的取值可以视为一个向量V(x)=(v1(x),v2(x),…,vm(x)),因而欧氏距离不仅可用于度量任意2个对象之间的距离而且同样可用于度量2个集合之间的距离.基于欧氏距离,用以度量等价类与目标集合间相似度的欧氏距离描述如下. 给定一个信息系统S=(U,C∪D,V,f),其中,条件属性集合为C={c1,c2,…,cm},目标集合为X={x1,x2,…,x|X|},∀X⊆U.有限论域U上由等价关系IND(C)诱导的划分为UIND(C)={E1,E2,…,Es},则对于∀Ei(Ei∈UIND(C),i=1,2,…,s),等价类Ei和目标集X间的欧氏距离公式表示为 (13) 其中, 表示任意2个特征向量V(xi)=(v1(xi),v2(xi),…,vm(xi))和V(xj)=(v1(xj),v2(xj),…,vm(xj))之间的欧氏距离,且xi表示等价类Ei中任意对象,xj表示目标集X中的对象. 为了便于说明问题,所有例子所用的信息表中的数据都是数值型的,且每个属性的量纲都相同.对于存在非数值型数据的信息表,当前研究中有很多方法可以将字符型数据转换成数值型数据,如LDA[32]等方法.对于存在不同量纲属性的信息表,采用min-max标准化等方法对数据进行统一量纲处理即可. 例1.给定一个信息表S=(U,C∪D,V,f),其中,有限论域为U={x1,x2,x3,x4,x5,x6,x7,x8},条件属性集合为C={c1,c2,c3,c4},目标集合为X={x1,x2,x7,x8}.例1的信息表如表2所示: Table 2 Information Table of Example 1表2 例1的信息表 由等价关系IND(C)诱导的论域U上的划分为UIND(C)={E1,E2,E3,E4}={{x1,x3},{x2,x4},{x5,x6},{x7,x8}}.根据式(12),可以得到目标集合中任意对象xi(xi∈X,i=1,2,…,|X|)分别与任意等价类Ej(Ej∈UIND(C),j=1,2,3,4)中任意对象的距离值(为了行文的简洁,仅给出部分结果): d(V(xi),V(xi))=0,i=1,2,…,8, 然后,根据式(13),等价类E1,E2,E3,E4与目标集X之间的欧氏距离分别为 d(X,E1)=1.620 2,d(X,E2)=2.067 6, d(X,E3)=3.648 7,d(X,E4)=1.303 9. 考虑到不同等价类与目标集之间距离的不同,则可认为等价类之间是存在差异的.因此,每个等价类对应的损失函数也应该是不同的.进一步地,借助例2阐述说明在构建综合评价函数以度量风险时考虑等价类之间的差异性能提高分类器性能的原因. 例2.根据例1,各等价类与目标集合的欧氏距离分别为d(X,E1)=1.620 2,d(X,E2)=2.067 6,d(X,E3)=3.648 7,d(X,E4)=1.303 9. 又目标集合为X={x1,x2,x7,x8},则对于等价类E1={x1,x3} 和E2={x2,x4},其粗糙隶属度均为Pr(X|E1)=Pr(X|E2) =0.500 0. 而由于d(X,E1)=1.620 2≠d(X,E2)= 2.067 6,所以二者与目标集的距离不同. 且d(X,E2)>d(X,E1),则相比于等价类E2,等价类E1与目标集合X更相似.换言之,尽管二者的粗糙隶属度相同,若仅有一个等价类能够被划分到正域,考虑到等价类之间的差异性,相比于等价类E2,等价类E1更应该被划分到正域. 根据例1和例2,由等价关系诱导的论域划分中的确存在一些与目标集合之间的相似度不相同的等价类,即相对于目标集合来说,等价类之间确实存在差异.因此,在度量风险时,应该对这些等价类有所区分.另外,根据3WD-DTRSs模型[11-12],由于根据专家经验给定的损失函数面向整个论域,即对于任意等价类,其损失函数集合均相同,从而在贝叶斯决策准则下推导的阈值并不能使得所有等价类达到全局最优划分. 在决策过程中,决策者一般通过综合考虑各条件属性而进行决策计划的制定.因此,提出了一种获取信息表中属性权重的方法.给定一个信息表S=(U,C∪D,V,f),可以得到论域U中所有对象x在条件属性ci上的取值,不妨表示为集合Vi={vi(x)|x∈U}.考虑到集合Vi的离散程度越大,则属性ci对论域U的划分能力越好,因此,采用方差来度量条件属性的权重,样本方差描述为: 设x1,x2,…,xn为取自某总体X的样本,则它关于样本均值的样本方差(平均偏差平方和)为 (14) 定义4.基于方差的属性权重. 给定一个信息系统S=(U,C∪D,V,f),其中,条件属性集合为C={c1,c2,…,cm},目标集合为X(X⊆U).则对于∀ci(ci∈C,i= 1,2,…,m),基于方差的属性权重函数可定义为 (15) 例3.给定一个信息系统S=(U,C∪D,V,f),其中,论域为U={x1,x2,x3,x4,x5,x6,x7,x8},条件属性集合为C={c1,c2,c3,c4},目标集合为X={x1,x2,x7,x8}.例3的信息表如表3所示: Table 3 Information Table of Example 3表3 例3的信息表 根据表3,条件属性c1对应的条件属性值集合为V1={v1(x)|x∈U}={3,1,3,1,3,3,3,3},则根据式(14),条件属性c1对应的条件属性值集合V1的集合方差为var(V1)=0.857 1.同理,条件属性c2,c3,c4对应的条件属性值集合V2,V3,V4的集合方差分别为var(V2)=0.285 7,var(V3)=0.125 0,var(V4)=0.982 1.再根据式(15),条件属性c1,c2,c3,c4的权重分别为 ω1=0.381 0, 如前所述,在说明等价类与目标集合之间存在差异这个问题时,为便于简单直接地说明问题,所采用的是简单的欧氏距离公式.然而,在使用欧氏距离度量等价类与目标集合的差异时,会存在2个等价类与目标集合在距离上相同的情况,而实际上2个等价类所对应的属性值集合是不同的情况.因此,为了将等价类之间由于属性值不同而产生的差异作为一个影响因子加入到风险度量的模型中,将基于集合相似度量方法[33]给出一种考虑等价类与目标集合之间差异性的综合评价函数以度量风险. 定义5.集合之间的相似度.[33]假设集合A和B是非空有限论域U上的2个子集,S:U×U→[0,1]是一个映射函数,即(A,B)→S(A,B).则S(A,B)是集合A和B之间的相似度函数,当且仅当S(A,B)满足4个条件: 1) 对于∀A,B⊆U,有0≤S(A,B)≤1; 2) 对于∀A,B⊆U,有S(A,B)=S(B,A); 3) 对于∀A,B⊆U,有S(A,A)=1; 4) 对于∀A,B⊆U,当且仅当A∩B=∅时,有S(A,B)=0. 定义6.改进的相似度量函数. 给定一个信息系统S=(U,C∪D,V,f),其中,条件属性集合为C={c1,c2,…,cm},目标集合为X(X⊆U). 则对于∀ci(ci∈C),∀Ej(Ej∈UIND(C))与目标集合X之间的改进的相似度量函数可定义为 (16) 其中,|·|表示集合的势,Ej表示由等价关系IND(C)在有限论域U上诱导的等价类,vi(Ej)表示等价类Ej在条件属性ci上的值,vi(x)表示任意对象x(x∈U)在条件属性ci上的取值. 将一个本属于目标集合的对象划分到正域带来的风险要小于将其划分到边界域所带来的风险,且将其划分到边界域带来的风险也小于将其划分到负域带来的风险,同理,对于一个本不属于目标集合的对象,同样有类似的规律.此外,对于目标集来说,任意等价类所对应的条件属性值与之越相似,则将该等价类划分到正域所产生的风险越小.因此,为使得评价函数满足以上规律,不妨借用对数函数的简洁形式,基于集合相似度量的概念,提出对条件属性值打分的评价函数的定义. 定义7.基于相似度量的评价函数. 给定一个信息系统S=(U,C∪D,V,f),其中,条件属性集合为C={c1,c2,…,cm},目标集合为X(X⊆U).则在任意划分情况δ(δ∈H,H={PP,BP,NP,NN,BN,PN})下,对于∀ci(ci∈C,i=1,2,…,m),基于相似度量的评价函数可定义为 (17) 其中,常数序列ηPP,ηBP,ηNP和ηPN,ηBN,ηNN是基于相似度量的评价函数的系数,且其须满足: 2<ηPP<ηBP<ηNP,2<ηNN<ηBN<ηPN. (18) 例4.给定一个信息系统S=(U,C∪D,V,f),其中,论域为U={x1,x2,x3,x4,x5,x6,x7,x8},条件属性集合为C={c1,c2,c3,c4},目标集合为X={x1,x2,x7,x8}.信息表的具体信息如例3中的表3所示. 由等价关系IND(C)诱导的论域U上的划分为UIND(C)={E1,E2,E3,E4}={{x1,x3},{x2,x4},{x5,x6,x7},{x8}}.根据定义6,在属性c1上,等价类E1与目标集合X之间的改进的相似度量函数为 根据定义7,不妨将基于相似度量的评价函数的系数取为ηPP=3.000 0,ηBP=5.000 0,ηNP=9.000 0,ηNN=3.500 0,ηBN=7.000 0,ηPN=12.000 0.则根据定义7,对于条件属性c1,在任意的划分情况δ(δ∈H)下,等价类E1={x1,x3}与目标集X之间基于相似度量的评价函数分别为 同理,对于条件属性c2,c3,c4,在任意划分情况δ(δ∈H)下,等价类E1={x1,x3}与目标集X之间的改进的相似度量函数分别为 ψc3(E1,X)=0.800 0, 同理,对于等价类E2,E3,E4,在任意条件属性下及任意划分情况下,基于相似度量的评价函数都可以计算. 性质1.给定一个信息表S=(U,C∪D,V,f),其中,条件属性集合为C={c1,c2,…,cm}.则给定∀ci(ci∈C,i=1,2,…,m)的条件下,对于∀Ej(Ej∈UIND(C)),基于相似度量的评价函数满足(-,+). 证明. 因为对于 ∀ci(ci∈C,i=1,2,…,m),∀Ej(Ej∈UIND(C))及给定的目标集合X(∀X⊆U),不等式0<ψci(Ej,X)≤1成立. 则当满足条件 2<ηPP<ηBP<ηNP,2<ηNN<ηBN<ηPN时,(-,+)成立. 证毕. 值得指出的是,对于给定的条件属性及在相同的划分动作下,评价值越高的等价类被划分到正域而产生的风险越小. 性质2.给定一个信息系统S=(U,C∪D,V,f),对于∀Ej(Ej∈UIND(C)),∀ci(ci∈C,i=1,2,…,m),如果常数序列满足条件(ηPN-ηBN)(ηNP-ηBP)>(ηBP-ηPP)(ηBN-ηNN),则基于相似度量的评价函数满足不等式 证毕. 性质3.给定一个信息系统S=(U,C∪D,V,f),对于∀Ej(Ej∈UIND(C)),∀ci(ci∈C,i=1,2,…,m),如果常数序列满足不等式 (ηPN-ηBN)(ηNP-ηBP)<(ηBP-ηPP)(ηBN-ηNN),则基于相似度量的评价函数满足不等式 证明. 证明过程类似于性质2. 决策者在做决策时一般是综合考虑每个对象的各条件属性,因此根据定义7,给出以下综合评价函数,以综合各条件属性的评价值. 定义8.综合评价函数.给定一个信息表S=(U,C∪D,V,f),其中,条件属性集合为C={c1,c2,…,cm},目标集合为X(X⊆U). 则对于 ∀Ej(Ej∈UIND(C)),任意划分情况δ(δ∈H)下的综合评价函数可以定义为 (19) 例5.根据例4,对于任意条件属性ci(ci∈C),已得到在任意划分情况δ(δ∈H)下,任意等价类Ej(Ej∈UIND(C))与目标集合X间的评价值.如对于等价类E1,相应的评价值为 根据例3,属性c1,c2,c3,c4的权重分别为ω1=0.381 0,ω2=0.127 0,ω3=0.055 6,ω4=0.436 5.因此,对于E1={x1,x3},在不同的划分情况δ(δ∈H)下的综合评价值分别为 μPP(E1)=2.582 4,μBP(E1)=3.604 1, 性质4.给定一个信息系统S=(U,C∪D,V,f),对于∀Ej(Ej∈UIND(C))及∀ci(ci∈C,i=1,2,…,m),若成立,则(μPN(Ej)-μBN(Ej))×(μNP(Ej)-μBP(Ej))-(μBP(Ej)-μPP(Ej))(μBN(Ej)-μNN(Ej))成立. 证明. 因为 从而 (μPN(Ej)-μBN(Ej))(μNP(Ej)-μBP(Ej))>(μBP(Ej)-μPP(Ej))(μBN(Ej)-μNN(Ej))成立. 证毕. 根据决策粗糙集模型[11-12],SBA-3WD-SF模型同样有2个状态T={X,X}及3个动作A={aP,aB,aN},则相应的综合评价函数可由表4表示: Table 4 Comprehensive Evaluation Function表4 综合评价函数 根据贝叶斯决策过程[11],采取不同动作aP,aB,aN时,对于∀Ej(Ej∈UIND(C)),基于相似度量的期望风险分别为 R(aP|Ej)=μPPPr(X|Ej)+μPNPr(X|Ej), R(aB|Ej)=μBPPr(X|Ej)+μBNPr(X|Ej), R(aN|Ej)=μNPPr(X|Ej)+μNNPr(X|Ej). (20) 根据贝叶斯决策准则,使得期望风险最小的一套动作,便是最优划分计划.从而,可得到3条决策规则: (P)如果R(aP|Ej)≤R(aB|Ej)且R(aP|Ej)≤R(aN|Ej),则Ej⊆POS(X); (B)如果R(aB|Ej)≤R(aP|Ej)且R(aB|Ej)≤R(aN|Ej),则Ej⊆BND(X); (N)如果R(aN|Ej)≤R(aP|Ej)且R(aN|Ej)≤R(aB|Ej),则Ej⊆NEG(X). 这3条决策规则只与判别函数Pr(X|Ej)及各综合评价函数有关.根据定义6及性质2,各综合评价函数满足条件μPP(Ej)<μBP(Ej)<μNP(Ej),μNN(Ej)<μBN(Ej)<μPN(Ej).因此,在此大小关系的前提下,使得决策风险最小的决策规则表示为 进一步,为了得到决策规则的简约形式,简记处理为 (21) 根据性质4,则有不等式: 而因为不等式: 成立,则有不等式: 成立,即0≤βj<γj<αj≤1成立.因此,规则(P)(B)(N)可以等价地表示为 (P)如果Pr(X|Ej)≥αj,则Ej⊆POS(X); (B)如果βj (N)如果Pr(X|Ej)≤βj,则Ej⊆NEG(X). 综上所述,根据决策规则,给出了一个阈值自适应的三支决策分类器. 根据2.1~2.3节,所提模型的基本步骤可由算法1,2,3表示.在算法1,2,3中,m表示条件属性的个数,ωi(i=1,2,…,m)表示每个条件属性的权重.δ(δ∈H)表示任意划分情况.Ej表示由等价关系IND(C)在论域U上诱导的划分UIND(C)中的任意等价类,s表示UIND(C)中的元素个数.pos,bnd,neg分别表示正域、边界域及负域. 算法1.计算每个条件属性的权重. 输入:S=(U,C∪D,V,f); 输出:ωi. ① fori=1 tom Temp+=var(Vi); ② end for ③ fori=1 tom ④ end for 算法2.构造综合评价函数. 输入:S=(U,C∪D,V,f),X,ωi,ηδ; 输出:μδ(Ej). ① for eachci∈C for eachEj∈UIND(C) ψci(Ej,X)= ② end for ③ end for ④ fori=1 tom while 2<ηPP<ηBP<ηNP&& 2<ηNN< ηBN<ηPN&& (ηPN-ηBN)(ηNP-ηBP)> (ηBP-ηPP)(ηBN-ηNN) do ⑥ end while ⑦ end for 算法3.计算模型的分类准确率(acc)及召回率(recall). 输入:S=(U,C∪D,V,f),X,μδ(Ej); 输出:acc,recall. ① 初始化pos=∅,bnd=∅,neg=∅. ② forj=1 tos and ③ ifPr(X|Ej)≥αjthen ④pos←pos∪Ej; ⑤ else ifβj ⑥bnd←bnd∪Ej; ⑦ elseneg←neg∪Ej; ⑧ end if ⑨ end for 通过分析算法1,2,3,所提算法的时间复杂度为T(n)=O(n2).因此,所提算法在现实生活中是有效可行的. 在垃圾邮件过滤领域,用户通常关心的是邮件正确分类数量占总体邮件的比例.当前评价垃圾邮件过滤器性能的方法中,常用的评价指标为准确率(acc)及召回率(recall)等[34]. 3.1.1 准确率 对于垃圾邮件过滤器,垃圾邮件被分到垃圾邮件类及合法邮件被分到合法邮件类的数量占邮件总量比例越高,则该过滤器的性能越好.因此,不妨采用准确率来衡量过滤器的性能. (22) 其中,ns→s表示实为垃圾邮件的对象被分为垃圾邮件类的数量,nl→l表示实为合法邮件的对象被分为合法邮件的数量,|U|表示论域中的所有邮件的数量. 3.1.2 召回率 对于垃圾邮件过滤器,垃圾邮件被划分到垃圾邮件类的占实际垃圾邮件比例越高,则说明该过滤器对垃圾邮件的识别能力越好,即过滤器的性能也越好.因此,不妨采用召回率来衡量过滤器的性能. (23) 其中,Ns表示实为垃圾邮件的对象个数. 相较于传统的二分类模型,由于三支决策模型增加了延迟决策域,则其能有效降低错误分类代价,从而有效提高分类的准确率.特别地,相较于3WD-DTRSs模型[11],所提的SBA-3WD-SF模型能提高准确率及召回率.为了验证这一点,使用当前垃圾邮件过滤研究领域的2个常用数据集,其一是来自UCI机器学习数据资料库的Spambase数据集,其二是来自文献[35]提供的PU1 Corpus数据集,二者的基本信息如表5所示: Table 5 Basic Information of Datasets表5 数据集基本信息 对于Spambase数据集,实验随机选取了3 000个样本作为训练数据集,剩下的1 601个样本作为测试数据集.首先,采用Entropy-MDL方法[36]对训练数据集及测试数据集进行离散化处理,然后选用条件互信息最大化法[37]对数据集进行特征选择,从57个条件属性中选取了20个条件属性.对于PU1 Corpus数据集,由于该语料库本身已被分为10个部分,因此实验随机选取了其中的8个部分作为训练数据集,剩下的2个部分作为测试数据集.进一步采用基于互信息的单变量特征提取方法(KBest feature selection)对数据集进行特征选择,并依据互信息最大化原则,选择了前200个条件属性. 为测试模型的性能,针对3WD-DTRSs模型[11]及所提SBA-3WD-SF模型,实验分别随机给出了5组参数如表6及表7所示.根据1.2节中二元NB分类器[30]的原理,其模型的阈值相应地可扩展表示为ξ=λNPλPN,如表8所示. Table 6 Loss Functions of 3WD-DTRSs Model[11]表6 3WD-DTRSs模型[11]的损失函数 Table 7 Coefficients of Evaluation Functions Based onSimilarity Measure Table 8 Threshold of Binary NB Classifier[30]表8 二元NB分类器[30]的阈值 首先,针对分类器的准确率,SBA-3WD-SF模型与二元NB分类器[30]及3WD-DTRSs模型[11]在数据集Spambase上的表现分别如图2(a)(b)所示.从图2(a)(b)中可以发现在Spambase数据集上,3WD-DTRSs模型及SBA-3WD-SF模型的分类准确率均优于二元NB模型,且SBA-3WD-SF模型要优于3WD-DTRSs模型.另外,如图3(a)(b)所示,可以发现3WD-DTRSs模型及SBA-3WD-SF模型的分类准确率均优于二元NB模型,且SBA-3WD-SF模型的分类准确率优于3WD-DTRSs模型. 其次,针对分类器的召回率,SBA-3WD-SF模型与二元NB分类器及3WD-DTRSs模型在数据集PU1 Corpus上的表现分别如图3(c)及图3(d)所示.在PU1 Corpus数据集上,3WD-DTRSs模型及SBA-3WD-SF模型的召回率均优于二元NB模型,且SBA-3WD-SF模型的召回率要优于3WD-DTRSs模型.在Spambase数据集上,如图2(c)(d)所示,3WD-DTRSs模型及SBA-3WD-SF模型的召回率均优于二元NB模型,且SBA-3WD-SF模型的召回率要优于3WD-DTRSs模型. Fig. 3 Results of comparative experiments on PU1 Corpus图3 PU1 Corpus数据上的对比结果 在表6~8中的任意参数条件下,3WD-DTRSs模型[11]及SBA-3WD-SF模型在Spambase或PU1 Corpus数据集上的分类准确率及召回率都要优于二元NB模型[30],且SBA-3WD-SF模型无论在分类准确率还是召回率上也同样明显优于3WD-DTRSs模型.而表6~8中的参数都是随机给定的,因此根据极大似然法原理,3WD-DTRSs模型及SBA-3WD-SF模型的分类准确率及召回率优于二元NB模型,且SBA-3WD-SF模型无论在分类准确率还是召回率上也同样明显优于3WD-DTRSs模型. 特别地,由于NB分类器为了求解后验概率而采用了特征条件独立性假设这一严格的条件,因此该模型牺牲了一定的分类准确率.值得指出的是,如图3(c)所示,NB模型的鲁棒性较差,而3WD-DTRSs及SBA-3WD-SF模型则具有良好的鲁棒性.此外,SBA-3WD-SF模型在3WD-DTRSs模型的基础上,在进行风险度量时考虑了等价类之间差异带来的影响,因此,在理论上,SBA-3WD-SF模型的分类准确率及召回率都优于3WD-DTRSs模型.而对于二分类及三支决策来说,从理论上,相较于二分类模型,三支决策模型由于增加了延迟决策域而能有效降低分类风险代价,从而提高模型的分类准确率及召回率等.从实验结果上来看,由图2和图3可知在2个垃圾邮件分类的数据集上,SBA-3WD-SF模型及3WD-DTRSs模型的分类准确率及召回率的确都优于二元NB模型,SBA-3WD-SF模型也要明显优于3WD-DTRSs模型.此外,由图2(b)(d)、图3(b)(d)可以发现,在Spambase或者PU1 Corpus数据集上,所提模型SBA-3WD-SF相较于3WD-DTRSs模型来说,分类准确率及召回率提高的幅度没有特别大,而在垃圾邮件过滤领域,即使只有一封邮件被错误分类都会产生不可估量的代价.因此,在垃圾邮件过滤领域,SBA-3WD-SF模型具有显著的价值. 垃圾邮件分类中分类准确率及召回率等是用户最为关注的问题.相较于二分类模型,增加了延迟决策域的三支决策模型能有效降低错分代价,从而提高分类准确率及召回率.通过度量等价类与目标集的距离,发现相对于目标集合来说,等价类之间的确存在差异.因此,在3WD-DTRSs模型的基础上提出了一种基于相似度量的阈值自适应三支垃圾邮件过滤模型.首先根据集合方差提出了一种计算条件属性权重的方法,然后考虑等价类之间的差异性带来的影响,基于等价类之间的相似度重新构建了综合评价函数,然后依据贝叶斯决策准则推导出自适应阈值.在垃圾邮件过滤领域,过滤器的性能至关重要.对比实验表明所提SBA-3WD-SF模型在分类准确率及召回率等指标上都优于3WD-DTRSs模型[11]及二元NB模型[30],即验证了SBA-3WD-SF模型的合理性及有效性,同时也说明了SBA-3WD-SF模型在垃圾邮件过滤领域的价值.值得提出的是,除了损失函数,影响垃圾邮件过滤器的性能的因素有很多,如判别函数及参数的求解方式等.因此,今后的研究工作将重点关注判定函数的合理构建及更优的参数求解方式.
2 基于相似度量的三支决策模型
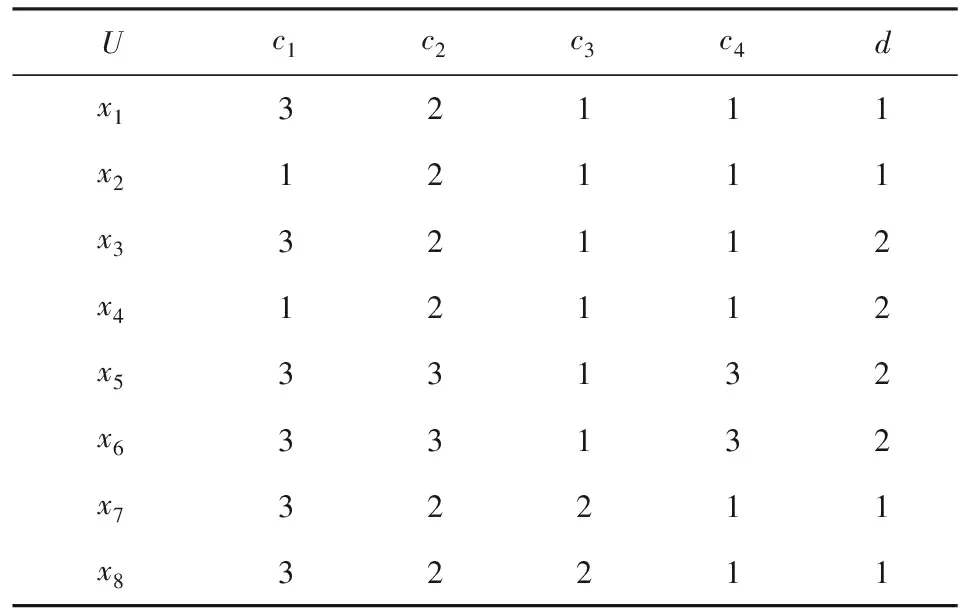
d(V(x1),V(x2))=2.160 3,
d(V(x1),V(x5))=3.582 4,
d(V(x2),V(x3))=2.857 8,
d(V(x2),V(x5))=4.183 4,
d(V(x2),V(x7))=3.055 1,
d(V(x6),V(x7))=2.645 8.2.1 基于方差的属性权重度量


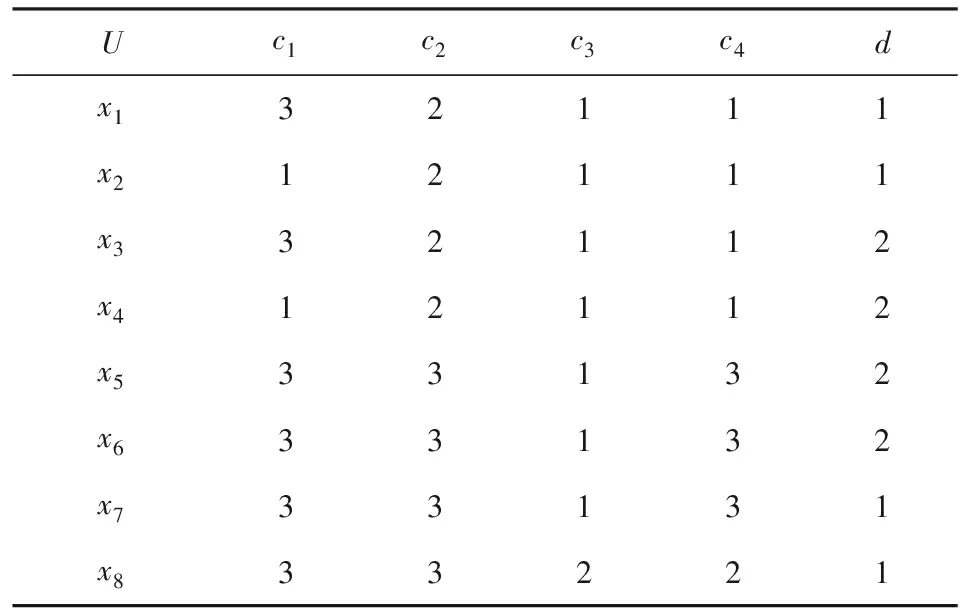
ω2=0.127 0,
ω3=0.055 6,
ω4=0.436 5.2.2 基于相似度量的风险度量

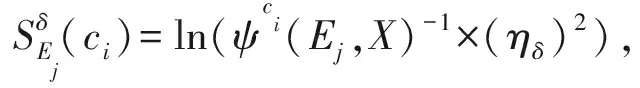
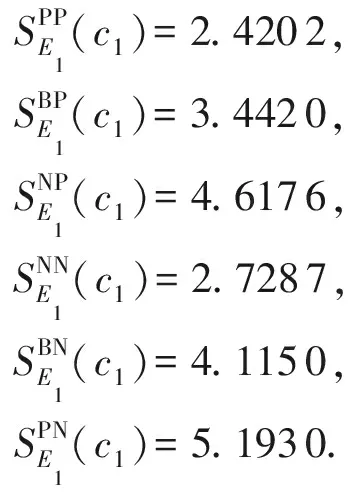
ψc4(E1,X)=0.600 0.
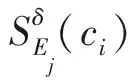
μNP(E1)=4.779 7,μNN(E1)=2.890 8,
μBN(E1)=4.277 0,μPN(E1)=5.355 0.
2.3 SBA-3WD-SF模型阈值推导


2.4 算法步骤
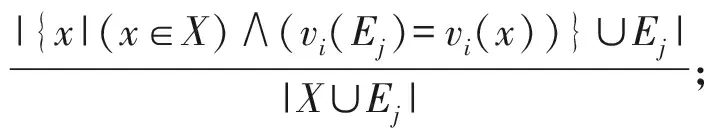

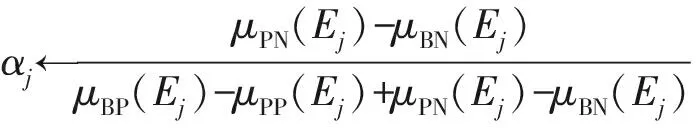

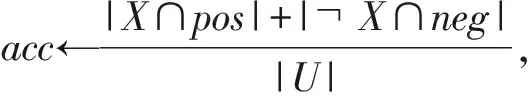
3 对比实验
3.1 实验指标


3.2 数据预处理与参数设置


3.3 实验结果与分析
4 结 语
