LB上Volterra型与复合算子积的有界性与紧性关系
2019-11-14
(闽南理工学院信息管理学院,福建 石狮 362700)
1 预备知识
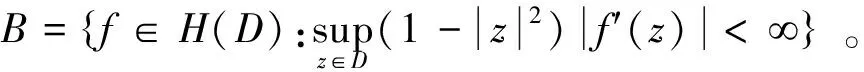
定义3现在定义LB是对数Bloch空间。如果
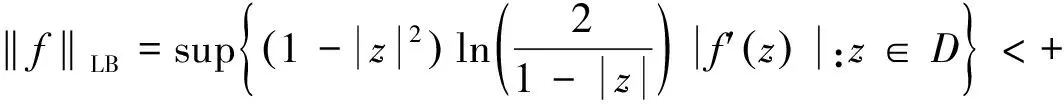
则f∈LB。
‖f‖LB是一个半范数(‖f‖L=|f(0)|+‖f‖LB),所以LB是一个Banach空间。
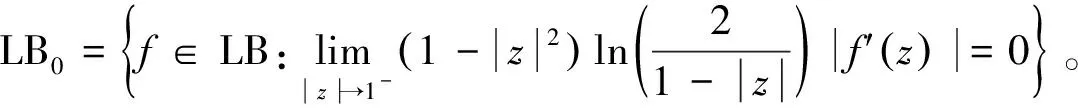
定义4设φ是D上的解析自映射,即φ∈S(D),那么将H(D)上的复合算子定义为Cφ(f)=f(φ(z)),f∈H(D),z∈D。显然Cφ是线性算子。
定义5令g∈H(D),对每个H(D)中的函数f,将Volterra型算子Jg,Ig分别定义为
随着经济的发展和科技的进步,短视频行业已经逐渐形成规模化运营,因此,政府的监管力度也随之加大。从2016年起,政府对网络短视频的监管力度加大,广电总局、文化部等多个部门与政府联手进行监管,为移动短视频的发展提供了规范发展的契机。
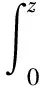
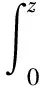
定义6定义Volterra型算子和复合算子的积如下:
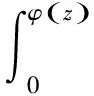
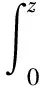
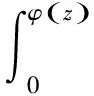
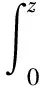
在文[2]中研究了从H和Bloch空间到Zygmund空间上的Volterra型算子和复合算子的积。本文将在LB和LB0上讨论这些算子的有界性之间的关系,以及在LB和LB0上它们的有界性和紧性这两者之间的关系。
2 主要结论
引理1(Motel定理) 若解析函数序列{fn(z)}(n=1,2,3…)在区域D内闭一致有界,则必有{fn(z)}的一个子序列{fnk(z)}(k=1,2,3…)在D内闭一致收敛。
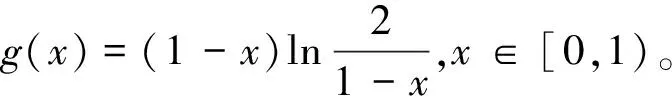
定理1假定f∈LB,则‖ft‖LB≤4‖f‖LB,0 证明 此定理的证明由引理2很容易得出。 定理2令g∈H(D),φ是D上的解析自映射。如果CφJg(或JgCφ,CφIg,IgCφ)是LB0上的一个有界算子,则CφJg(或JgCφ,CφIg,IgCφ)是LB上的有界算子。 证明 假定CφJg在LB0上是有界的。显然,对任意f∈LB,有ft∈LB0,对所有0 ‖CφJg(ft)‖L≤‖CφJg‖‖ft‖L≤4‖CφJg‖‖f‖L<+ 令t→1-,因此 ‖CφJg(f)‖L≤4‖CφJg‖‖f‖L<+ 这就证得:CφJg在LB上有界。类似地,可证得JgCφ,CφIg,IgCφ是LB上的一个有界算子。 定理3假定CφJg(或JgCφ,CφIg,IgCφ):LB→LB是LB上的有界算子,则CφJg(或JgCφ,CφIg,IgCφ): LB→LB是紧的当且仅当对任意满足在D的紧子集上有fn一致收敛于0的序列{fn}(⊂LB), 则有 ‖CφJg(fn)‖L→0 (或‖JgCφ(fn)‖L,‖CφIg(fn)‖L,‖IgCφ(fn)‖L→0),当n→时。 证明“⟹”这个结论显然成立。 “⟸”假设CφJg不是紧的,则存在序列{fn}(⊂LB),使CφJg(fn)中任意的序列都不收敛。但由于CφJg是LB上的有界算子,且任意满足在D的紧子集上有fn一致收敛于0的序列{fn}(⊂LB)。由Motel定理知:存在{fnk}使{CφJg(fnk)}收敛,这与假设矛盾,故原结论成立。由此可证:CφJg是紧的。同理可证JgCφ,CφIg,IgCφ是紧的。 定理4令U⊂LB0,则U是紧的当且仅当U是闭的,有界的且满足 证明此证明类似于文献[2]中引理1的证明。
