一类交叉扩散系统稳态解的存在性和多重性
2019-11-13曾纯一
曾纯一
(西南民族大学预科教育学院,四川 成都 610041)
反应扩散现象与人们的生活密切相关,它能描述客观事物的主要特征及发展规律,相对于常微分方程所描述的有限维动力系统而言,反应扩散方程所刻画的动力系统的动力学性质更为复杂,特别是带有交叉扩散的各类生物、生态系统模型,由于从非线性的角度,交叉扩散系统是属于拟线性抛物系统,关于这类系统的非平凡解的存在性问题已有一些结果,但很少有人讨论具有自扩散和交叉扩散的生态模型的分岔现象,近年来带有交叉扩散的各类生物、生态模型[1-6]备受关注,主要研究了非常数稳态解的不存在性和存在性,后来也有不少作者研究了交叉扩散系统[7-9]和带时滞的反应扩散方程系统的动力学行为[10-14],扩散一般分为自扩散、自由扩散和交叉扩散,考虑到交叉扩散对生物、生态系统的平衡态的影响非常有必要,而且也是十分有意思的一件事情,接下来,将利用一种新方法来研究如下一类具有交叉扩散影响的沙漠化生态模型:

其中d,β,P,α,r,σ 和ρ 均为正常数,具体含义见参考文献[1],系统(1)显然有稳态解(u,v)=(P,0),接下来在P=ρ 的前提下,把(P,0)平移到(0,0),然后将主要运用文献[15]中的Lyapunov-Schmidt 约化方法来研究在Dirichlet 边界条件下的新系统在(0,0)点附近的空间非齐次稳态解的存在性、多重性及解的具体表示式.
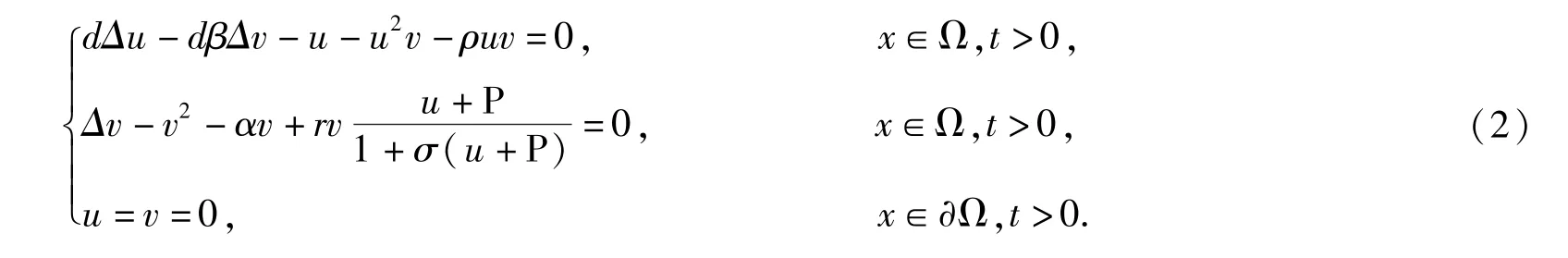
1 预备知识
为了方便,本文中总假设λi(i∈N)为下面特征值问题的单重特征根.

其中φn是特征值λn所对应的特征向量,且为定义在Ω 上的可积函数空间L2(Ω)的完备的标准正交系,满足且φ1(x)>0.记φ∗=φ1,为了方便,本文所讨论的空间L2(Ω),Hk(Ω),为标准实值Sobolev 空间,记,以对所有的x∈∂Ω}.对任意的X 和Y 的子空间Z,定义Z 的复值空间
对线性算子L:Z1→Z2,记L 的定义域为Dom(L),记L 的值域为Range(L).
接下来,首先研究系统(2)的空间非齐次稳态解的存在性,系统(2)的稳态解满足如下的边值问题:
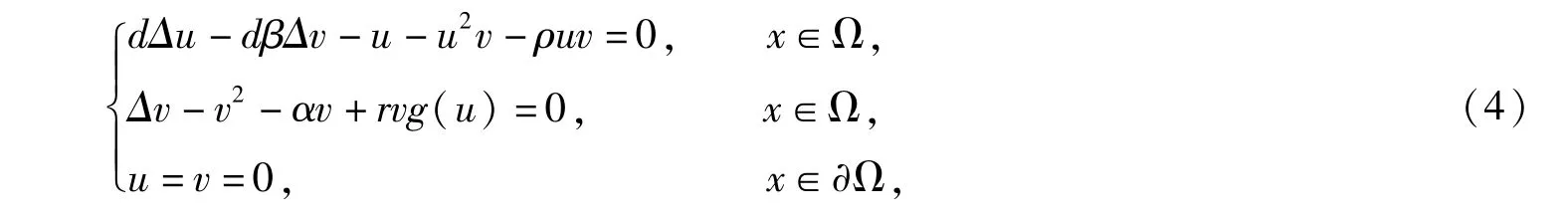

其中U=(u,v)T∈X2和λ∈R.接下来希望找到U∈X2和参数λ∈R 使得方程F(U,λ)=0.易知,对每一个固定参数λ∈R,F(U,λ)=0 都有一个平凡解U0=(0,0)T,即F(U0,λ)=0 对任意的λ 结论均成立.为了进一步探讨U0附近系统(4)的非常数解的存在性,要先计算F 关于U 在(U0,λ)处Fréchet 导数,即

接下来需要计算算子Lλ的核,也即是说要解下面的方程于是有以下结论.
引理1 对每一个固定的λ,算子Lλ∗的核为K=span{q},其中q=(aφ∗,φ∗)T且
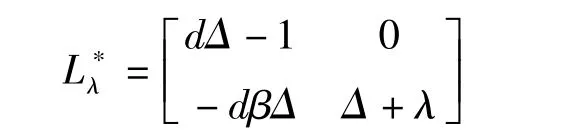
引理2 对每一个固定的λ,算子的核为K∗=span{p},其中p=(0,φ∗)T.
2 主要结论
本文的主要目的是找到非线性方程F(U,λ)=0 的非零解,并且满足当参数λ 趋于λ∗时有U 趋于U0.为了运用Lyapunov-Schmidt 约化方法得到一个有限维的分岔问题.首先对空间进行分解:


对于每个U∈X2,有唯一的分解U=kq+W,其中,k∈R 且,记I(k,W,λ)=PF(kq+W,λ),即,显然有,I(0,0,λ)=0 和.运用隐函数存在定理,显然可以获得一个连续可微映射使得W(0,λ∗)=0 且PF(kq+W(k,λ),λ),其中,W(k,λ)=(W1(k,λ),W2(k,λ))T,所有的(k,λ)∈N×Θ,N 是向量0 在R2中的一个开邻域,Θ 是λ∗在R 中的一个开邻域.令其中ζ=(ζ1,ζ2)T和ξ=(ξ1,ξ2)T∈K,由计算得,
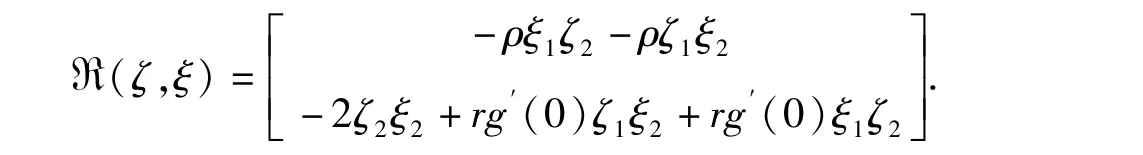
由(6)的第一个方程知:PR(q,q)+Lλ∗Wkk=0,因此,其中,Wkk=(W1,kk,W2,kk)T.
将W=W(k,λ)代入系统(6)的第二个方程得到
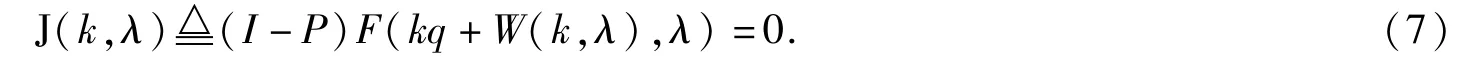
于是,接下来只需解方程J(k,λ)=0.将方程(7)与p=(0,φ∗)T做内积可以得到

显然,G(0,λ)=0,经计算易得算子G:R2→R 满足如下的表达式

下面将分两种情形得到系统(4)的空间非齐次稳态解存在性和多重性的结论.首先先考虑A0 的情形,运用隐函数存在定理可知存在一常数δ >0 和一个连续可微映射k:(λ∗-δ,λ∗+δ)→R,使得G(kλ,λ)≡0.即有

于是有以下结论:
定理1 如果,那么存在常数δ >0 和由(λ∗-δ,λ∗+δ)到R 的连续可微映射λ→kλ,使得系统(4)具有一个非平凡解Uλ=kλq+W(kλ,λ),而且由和W(0,λ∗)=0,该非平凡解满足
注解1 注意到λ∗是一维特征值问题(3)的主特征值,它在Ω 上对应的特征函数为φ∗>0,于是当(λ∗-λ)A >0((λ∗-λ)A <0)时,由定理1 得到的空间非齐次稳态解Uλ是正的(负的).由于在生物生态学中,负的稳态解没有意义,所以往往只研究正的稳态解.
定理2 如果A=0 且B <0(B >0),那么存在常数λ∗>λ∗(λ∗<λ∗)和由(λ∗,λ∗)到R(由(λ∗,λ∗)到R)的两个连续可微映射,使得系统(4)具有两个非平凡解,并且非平凡解满足
注解2 注意到λ∗是一维特征值问题(3)的主特征值,它在Ω 上对应的特征函数为φ∗>0,因此定理2 中得到的两个空间非齐次稳态解一个是正的而另一个是负的.在生物生态学中,只对其中正的那个稳态解感兴趣.
