带有脉冲和收获项的时滞Crowly-Martin型食饵-捕食系统的四个正周期解

吕小俊，谢海平，吕鹏辉

(云南大学旅游文化学院信息学院，云南 丽江 674199)

1 引言

在自然界中，捕食行为是很普遍的生物现象，所以利用食饵-捕食系统去描述生物种群的特征是有意义的.食饵-捕食系统由Lotka 和Volterra 在1926 年第一次提出，由于种群保护、维持生态平衡和种群管理等都依赖于食饵-捕食系统的动力学特征，所以研究食饵-捕食系统的动力学特征已成为一个新的热点，并得到很多优秀的结论[1-3，10-15].在传统Lotka-Volterra 模型中，生物学家发现捕食率不仅只依赖于食饵和捕食者种群密度的乘积，最终由Holling 提出功能反应函数的概念，功能反应函数反映捕食者在单位时间内捕食食饵的数量.并逐步提出各种类型的功能反应函数，例如Holling 型、Beddington-DeAngelis 型、Hassell-Varley 型和Crowly-Martin 型等.近年来，诸多学者已研究了带有功能反应函数的食饵-捕食系统的周期解、概周期解、多解和稳定性等问题[3-4，9-11].

另外，生物种群在自然界中受到地震、洪水、干旱和人类干扰等突发因素的影响，从而影响生物种群的动力学特征.在生物数学中，人们利用脉冲来描述这类突发干扰，故脉冲生态系统倍受众多学者的关注，并得到很多优秀的成果(见文献[3，6，7，10]).在文献[3]中，作者利用积分中值定理和李亚普诺夫函数研究了以下带有脉冲和时滞的食饵-捕食系统(1)的概周期解，并得到该系统存在唯一稳定概周期解的充分条件.

同时，随着人类经济社会的高速发展，生物资源的开发和对种群数量的定期收获已被广泛应用于渔业和野生动物管理中，因此，在食饵捕食系统中增加收获项是有必要的.且收获项会影响生物种群的多个周期和概周期现象(见文献[5-6，9]).据作者所知，至今很少有人研究带有脉冲和收获项的Crowly-Martin 型食饵-捕食系统的多解性问题.

受以上启发，在本文中，利用一般连续定理和一些微积分技巧，研究脉冲影响的时滞Crowly-Martin 型食饵-捕食系统(2)的多解性.

这里:x(t)和y(t)分别表示t 时刻捕食者和食饵的种群密度，ri(t)表示内部增长率，di(t)表示相互的种群密度阻力，hi(t)＞0 表示收获速率，i=1，2. τj1(t)(j1=1，2，3，4)表示非负变时滞函数， { tk}k∈N+是一个严格递增的序列存在d2k.

2 预备知识

介绍一些基本概念和引理:

引理1[8](一般连续定理)若X 和Z 均为Banach 空间，L:DomL⊂X→Z 是一个零指标的Fredholm 算子，N:，(x，λ)→N(x，λ)是一个L-压缩算子，连续映射P:X→X 和Q:Z→Z 满足:ImP=Ker L，ImL=Ker Q=Im(I-Q)，J:ImQ→Ker L 是一个同构映射.

(a)对于任意λ∈(0，1)，x∈∂Ω∩DomL，有Lx≠λN(x，λ)；

(b)对于任意x∈∂Ω∩KerL，有QN(x，0)≠0；

则对于任意的λ∈[0，1)，方程Lx=λN(x，λ)在集合Ω 上至少存在一个解，方程Lx=N(x，1)在Ω上至少存在一个解.

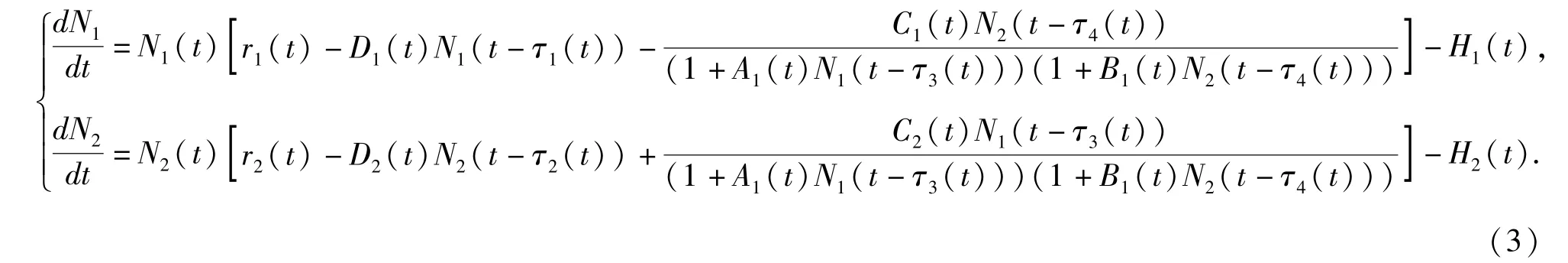
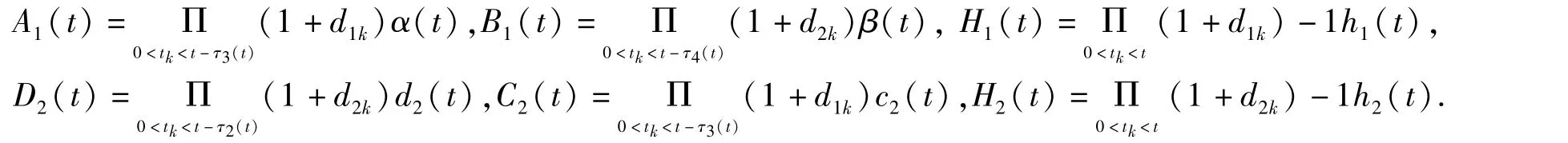
引理2 对于系统(2)和(3)，以下结论成立:

1)如果(N1(t)，N2(t))T是系统(3)的一个解，则

2)如果(x(t)，y(t))T是系统(2)的一个解，则

证明:该定理的证明过程和参考文献[6]中引理3 类似，故在此不再重复.

为了方便，介绍一些概念:

为了分析脉冲时滞Crowly-Martin 型食饵-捕食系统(2)的多解性问题，需作如下假设:

(H1)ri(t)，di(t)，hi(t)，ci(t)，α(t)，β(t)，τj1(t)(i=1，2，j1=1，2，3，4)均为有界非负的ω 周期函数，dj2k＞-1(j2=1，2，k∈N+).

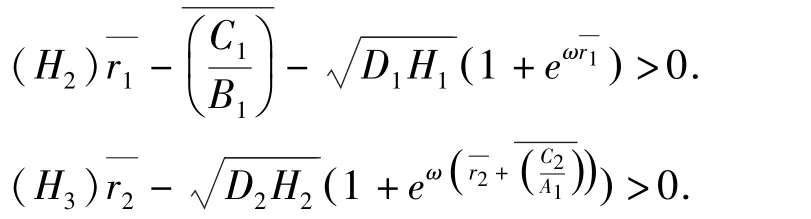
引理3 对于等式，如果条件(H2)和(H3)成立，则以下的不等式成立.

证明:该引理的证明过程和参考文献[5]中的引理2 类似，故在此不再重复.

3 主要结论

定理1 如果条件 (H1)- (H3)成立，则系统(2)至少存在四个ω-正周期解.

证明:由指数变换N1(t)=eu(t)，N2(t)=ev(t)，重新改写系统(3)为:

这里:

这里，

显然，算子QN 和Kp(I-Q)N 是连续的，对于任意的有界开集Ω⊂X，和是相对压缩的，N 是集合上L-压缩的.

假设u=(u，v)T∈X 是系统Lu=λN(u，λ)的一个ω-正周期解，其中λ∈(0，1)，则存在ξi，ηi∈[0，ω]，满足:

首先，对方程Lu=λN(u，λ)左右两边均从0 到ω 积分，可得:

从而，

因此，

结合不等式(6)和(7)，可得:

故，

因此，∀t∈[0，ω]，有

同理，由等式(5)的第二个式子，可得:

因此，

再次，由等式(5)的第二个式子，可得:

又因为，∀t∈[0，ω]，有

由不等式(9)和(10)，∀t∈[0，ω]，有

进一步，分析等式(5)的第一个式子，可得:

由条件 (H2)，不难验证.故或

进一步，可得:

由条件 (H3)，不难验证.故或

现构造四个不同的有界开区域Ωi⊂X(i=1，2，3，4).

接下来，验证引理1 中(b)的条件成立.利用反证法，假设当u=(u，v)T∈∂Ωi∩R2(i=1，2，3，4)时，QN(u，0)=0 成立，即常向量u=(u，v)T∈∂Ωi∩R2满足:

最后，验证引理1 中(c)的条件成立.接下来，考虑系统(14)的四个不同的解:(u1，v1)=(u+，v+)，(，=(u-，v-)，() =(u+，v-)，这 里u±=v±==

由于KerL=ImQ，令J=I，由Leray-Schauder 度的定义可得:∀i=1，2，3，4，有

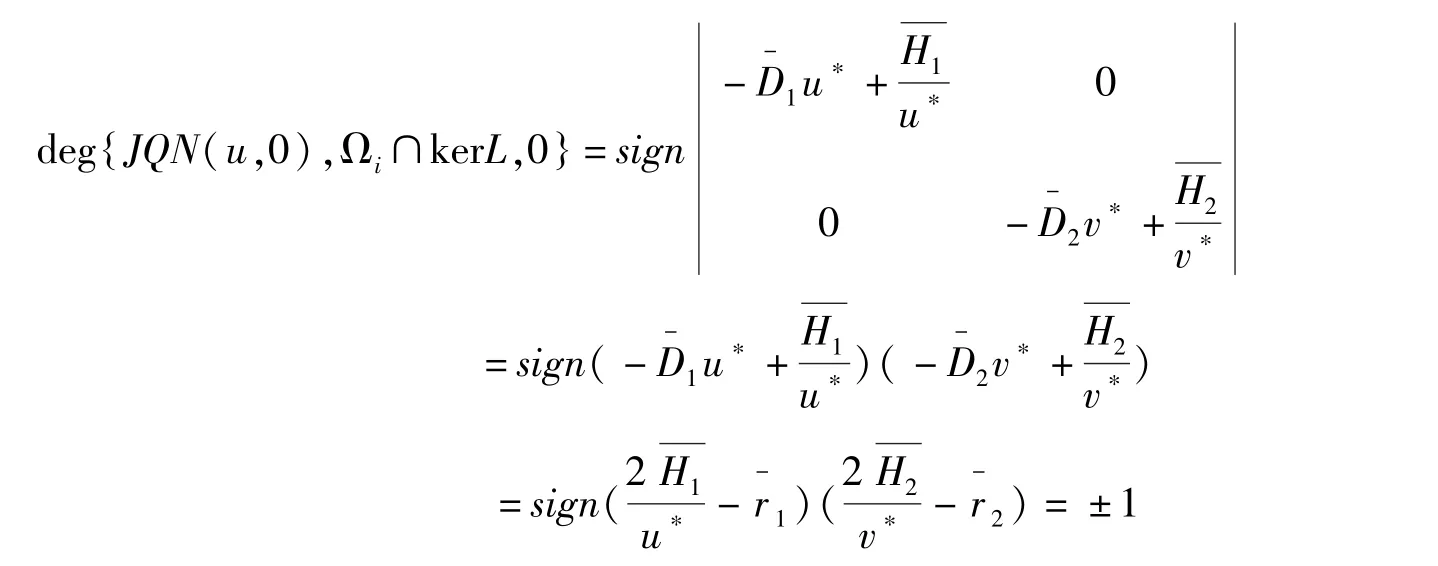
因此，引理1 中条件(c)成立.

综上分析可知，系统(3)至少存在四个不同的ω-正周期解.结合引理2，进一步获得脉冲时滞Crowly-Martin 型食饵-捕食系统(2)至少存在四个不同的ω-正周期解.证毕.

推论1 如果条件(和(成立，则带有脉冲的时滞Crowly-Martin 型食饵-捕食系统(1)至少存在一个正ω-周期解.其中

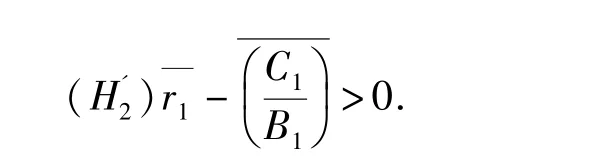
说明:当h1(t)=h2(t)=0 时，利用定理1 的证明方法，只能找到一个有效的有界开区域Ω，无法找到4 个不同的有界开区域Ωi(i=1，2，3，4)，故并不能得到系统(1)存在四个不同的正周期解.因此，收获项会影响脉冲时滞Crowly-Martin 型食饵-捕食系统(1)的多个正周期规则.

推论2 如果条件()，(H2)和(H3)成立，则带有脉冲和收获项的Crowly-Martin 型食饵-捕食系统(4)至少存在四个不同的正ω-周期解.其中:

说明:由定理1 的证明过程可知，时滞项τj1(t)(j1=1，2，3，4)不影响系统(2)的多个正周期规则.因此，系统(4)也至少存在四个不同的正ω-周期解.

4 例子

例1 分析时滞Crowly-Martin 型食饵-捕食系统(3)存在多个正周期解.其中，