关于球面单演函数的博克纳公式

李珊珊

(西南民族大学计算机科学与技术学院，四川 成都 610041)

1 引言

经典的傅里叶变换在基础数学和应用数学中是非常重要的.但在信号处理领域，源于电信技术的多道传输现在已经广泛应用于电子技术、通信、数字视频、计算机网络的各个方面，这促使我们去研究和发展向量值函数f=(f1，f2，…，fN)的函数理论.从数学的角度来说，多道传输的思想就是将N 个相互独立的函数fj∈L2(Rd；C)，j=1，2，…，N，编码成一个能捕捉每个分量信息的向量值函数f[1-4].众所周知，克里佛德代数是由d 个正规正交基{e1，e2，…，ed}生成的维数为2d的非交换代数，它给我们提供了一种具体方法来表示向量值函数.而克里佛德分析[5-6]是对欧氏空间Rd上的调和分析[7]的一种推广，从代数的背景来说，经典的调和分析是基于拉普拉斯算子Δ 和平方模生成的李代数sl2，克里佛德分析是将经典的李代数sl2改进成超李代数(它包含sl2作为其偶子代数).

如何将经典的傅里叶变换推广到克里佛德分析中是近年来的热点研究课题，关于此问题的讨论已经有许多的推广结果[8-12].在本文中，考虑的是最早出现在文献[13]中，并且在文献[14]得到进一步发展的一种基于超李代数的克里佛德-傅里叶变换(以下简记为CFT).它推广了经典的傅里叶变换，但它包含了生成子代数具体来讲，记为克里佛德分析中的迪拉克(Dirac)算子，则CFT 可以表示为下面的积分形式:

在分析学中，将一个复杂的函数空间分解成简单的子空间的直和，并且子空间在某种变换下保持不变是很重要的课题，基于文献[14]和[15]中球面单演函数理论，考虑将空间L2(Rd)分解成若干子空间的直和，其在CFT 下是保持不变的.这一步一般来讲是容易的，但是CFT 是如何作用在每个子空间上的是比较困难的问题.本文的主要目的是得到了CFT 作用在L2(Rd)的每个子空间函数的具体表达形式，这推广了经典球调和分析中的博克纳公式以及李子代数情况下的球面单演函数.

2 预备知识

假设{e1，e2，…，ed}是d 维欧式空间Rd的正规正交基，且满足下列反交换关系:

这里δjk是克罗内克(Kronecker)符号.复克里佛德代数Cl0，d是定义为维数是2d的结合代数，并且基为e0=1 和eA=eh1eh2…ehn，这里A={h1，h2，…，hn}⊂{1，2，…，d}，且1 ≤h1＜h2＜…＜hn≤d.这样，任一x∈Cl0，d可以表示为x=∑AxAeA，xA∈ℂ，这里ℂ 表示复平面.复克里佛德代数Cl0，d是复线性的、结合的但非交换的代数.

Rd中的元素可表示为x=x1e1+x2e2+…+xded，xj∈ℝ，j=1，2，…，d.Rd中两个向量的内积和外积定义如下:

上述表达式中向量x 和y 的乘积用公式(2)来定义.如果定义任一a∈Cl0，d的克里佛德共轭如下:

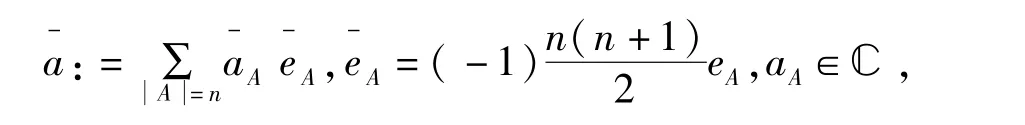
若在公式(3)中取f=g，可得任一f∈Cl0，d的模为

注意到向量x∈ℝd平方是数值的，并且等于它的范数的平方的相反数.一般来讲，对于任意a，b∈Cl0，d，有和但如果a∈ℝd和b∈Cl0，d，可推出

记Lp(ℝd；Cl0，d)为所有克里佛德值的函数f:ℝd→Cl0，d所构成的空间且有如下定义的有限范数

这里dx=dx1…dxd表示ℝd中的勒贝格测度.特别地，L2(ℝd；Cl0，d)中的内积定义为

这里注意到:若公式(7)中的函数f 和g 取复数值，则上述内积退化成L2(ℝd；Cl0，d)的子空间L2(ℝd；ℂ)的标准内积，即，

现在考虑文献[13]和[14]中引入的克里佛德-傅里叶变换(以下简记为CFT)的定义和基本性质:

定义2.1 记S(ℝd；Cl0，d)为克里佛德值的施瓦兹(Schwartz)函数类，定义f∈S(ℝd；Cl0，d)的CFT 如下:

它相应的逆变换为:

这里

和

注意到上面的核函数关于变量x，y 不是对称的，即，K-(x，y)≠K-(y，x)[11].所以约定积分时都对核函数的第一个变量进行积分.在本文中，只考虑核函数，其他的情形可以类似得到.

由文献[14]，使用盖根堡(Gegenbauer)多项式和贝塞尔函数Jα(t):

其中

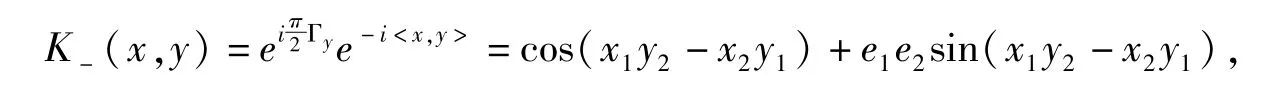
由于(e1e2)2=-1，上式中若用虚数单位i 代替e1e2，该核函数就相当于经典傅里叶变换中的核函数.但在高维的空间中，情况将变得很复杂.比如，在文献[14]中，作者证明了d ＞2 时，进一步，在维数为偶数的情况下，核函数又可表示为贝塞尔函数的有限和的形式:

注意到，当维数d 是偶数时，Aλ，Bλ和Cλ是实值的.而当d=2 时，核函数可由下式给出

上面偶数情形下的具体表达式使得文献[14]的作者去研究这个核函数的界，这就是下面这个引理.

引理2.2 设d 是偶数，对x，y∈ℝd，有

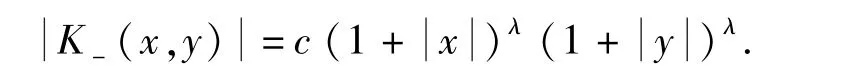
3 单演函数的博克纳公式

在这一小节里，考虑单演函数的博克纳公式.

定义3.1 设k∈ℕ.记

(iv)Hk为Rd中球面调和函数空间.

因为在偶数维数情况下，核函数K-(x，y)都是有界的.所以文献[14]给出了CFT 的一些重要性质:

引理3.2 假设Mk∈Μk和是S(ℝd；Cl0，d)中的实值径向函数，此外，记，则

由克里佛德代数知，对任一k∈ℕ，有

定义3.3 定义

(i)k≥0 时，Ωk为形如P(x)f(r)的有限线性复合函数，这里P∈Μk，f 是定义在[0，+∞)上的函数，满足

(ii)k ＞0 时，Ω-k为形如Q(x)g(r)的有限线性复合函数，这里是定义在[0，+∞)上的函数，满足∫

使用文献[16]和[15]中类似的结论，可以得到L2(ℝd；Cl0，d)的如下直和分解定理:

定理3.4 直和分解公式

在下述意义下成立:

(i)每一个子空间Ωk都是闭的；

(ii)Ωk是两两正交的；

(iii)L2(ℝd；Cl0，d)中每个元素是空间中有限线性复合的极限.

由文献[16]中L2(ℝd)的直和分解公式和公式(16)，这个定理易证.

在下面主要考虑CFT 如何作用在每个子空间Ωk上，，这里表示整数集.

定理3.5 每一个Ωk在CFT 下保持不变.准确地说，令f∈Ωk，和f(x)=R(x)h(r)，这里如果k≥0，则；如果k ＜0，则.有

并且

证明：当k≥0 时，因为，由公式(15)可得

F-f(x)=R(x)H(s)，

且

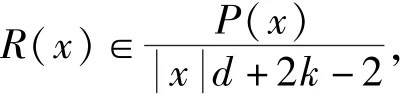
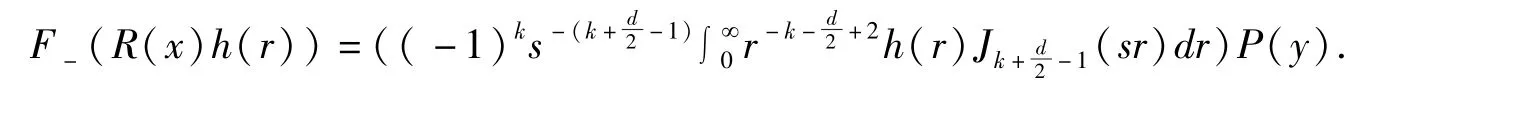
这样，就得到

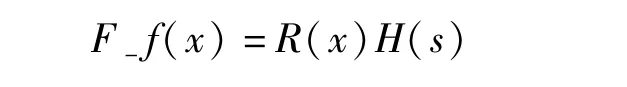
且

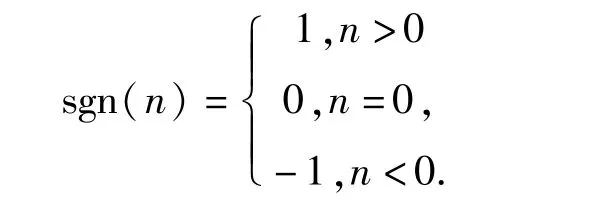
公式(18)和(19)可以统一为一个公式，即公式(17)，这样证明完成.