基于DirectX的六维控制器虚拟仿真

张彦斐，陈 超，宫金良

(山东理工大学 机械工程学院, 山东 淄博 255049)

并联机构具有刚度大、精度高等诸多优点，目前已经逐渐应用到各个领域，包括并联机床、微操作机器人、误差补偿器、多维控制器等。并联机构的运动学建模是控制系统设计的前提条件，相应建模方法较多，很多学者对此进行了深入研究[1-3]。陈宇航等[4]基于旋量运算得到子闭环中任意两构件的相对速度和加速度，解决了含有子闭环的并联机构动学建模问题。耿明超等[5]提出一种拟Newton法，提高了并联机构运动学正解的计算效率，并有效提高了实时性。孙坚等[6]借助Matlab中SimMechanics模块的系统动态建模功能，对Stewart平台进行了运动学和动力学分析，避免了复杂的建模过程。另外，基于ADAMS软件可以进行虚拟样机的试验和测试，也能够有效简化并联机构的分析方法[7-8]。如张静等[9]应用Inventor软件建立几何模型，以Parasolid格式导入ADAMS环境，对3-UPS/UP并联机构进行了运动学仿真;贾小刚等[10]结合ADAMS与Pro/E软件对并联机构的虚拟样机进行了运动学分析。

本文提出一种基于宏动3-URS并联机构的六维控制器，建立相应的运动学模型，并利用DirectX技术和四元数表示的坐标系旋转变换，进行六维控制器的虚拟仿真试验。

1 3-URS并联机构

图1所示为一种基于宏动3-URS并联机构，利用光电旋转编码器测量角位移的六维控制器。机构利用3条完全相同且呈中心对称分布的支链，将静平台和动平台连接在一起。6套驱动电机分成3组安装在静平台上，分别为3个万向铰呈正交布置的两轴提供动力输入。六维控制器工作时，在力和力矩的作用下，动平台的位姿将会发生改变，各关节量也会发生相应的变化。光电旋转编码器输入改变的各关节变量，输出经过滤波、电平转换等调理之后的差分电压模拟量信号，再通过数据采集卡将其倍频处理后转换成供计算机分析处理的数字量信号。计算机把采集的各关节变量，利用运动学模型及控制算法进行解算，控制虚拟机器人实现关联运动和模拟动态仿真。

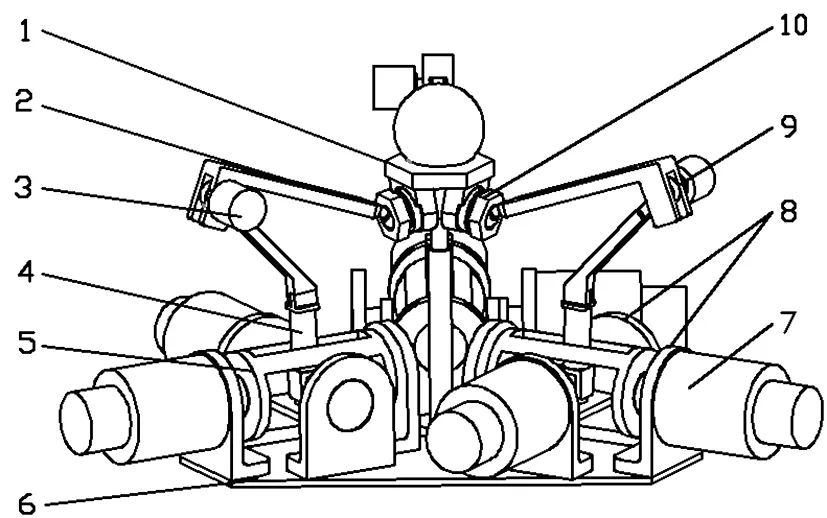
1.动平台；2.上连杆；3.光电编码器；4.下连杆；5.万向铰；6.静平台；7.力矩电机；8.安装基座；9.转动副；10.球铰图1 3-URS并联机构三维模型Fig.1 Three-dimensional model of 3-URS parallel mechanism

2 基于D-H方法的运动学建模

为便于建立3-URS并联机构的数学模型，将图1所示的三维模型进行简化处理，得到图2所示的3-URS并联机构原理简图，其中Ai(i=1,2,3)为万向铰两垂直交错轴的交点，Bi为每条支链末端球铰的中心点。在静平台中心固结参考坐标系{O}，Y轴正方向通过A1，Z轴垂直向上，X轴正方向由右手螺旋法则确定。在动平台中心固结动坐标系{O1}，初始位置各坐标轴的方向与参考坐标系一致。αi为绕X0轴的转角，βi为绕Z0轴的转角，γi为PiAi与PiBi之间的夹角，δ为PiAi与Z1轴之间的夹角，a为静平台的边长，b为动平台的边长。

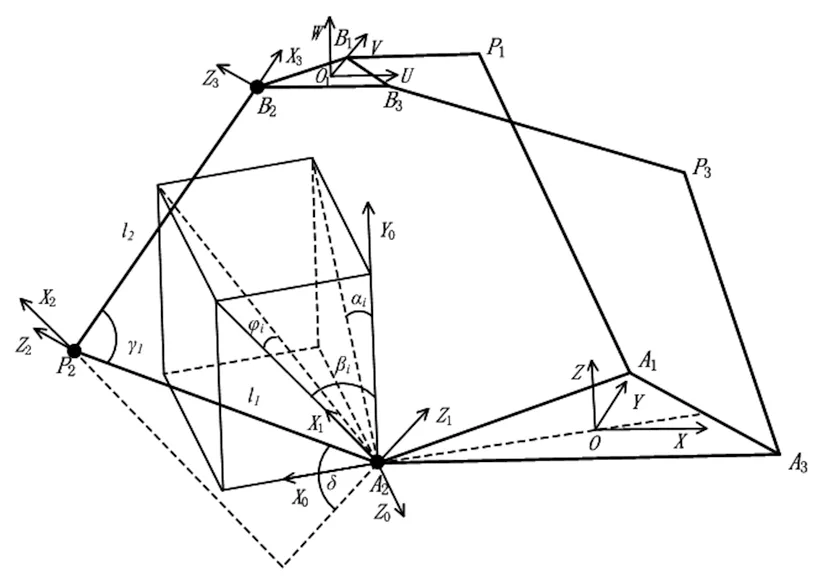
图2 3-URS并联机构原理简图Fig.2 Schematic diagram of 3-URS parallel mechanism

2.1 动平台运动学正解

采用D-H矩阵变换法对并联机构进行运动学建模。表1中给出了各连杆的D-H参数。

表1 D-H参数表
Tab.1 D-H Parameters

序号θdaα1π2+2i-1()3π0a3-π22-π2+βi()00π23-arctan(tanαicosβi)-l1cosδl1sinδπ24π2-γi-δ()0l20

相邻连杆之间的位姿关系可用坐标旋转和平移的方法建立联系，变换矩阵Ai为

式中，Sθi=sinθi，Cθi=cosθi。Bi点相对于参考坐标系的变换矩阵为

Ti=A1iA2iA3iA4i

(1)

在矩阵Ti中用位置矢量Bi=[pxipyipzi]T表示球铰中心Bi的位置，用旋转矩阵R=[noa]表示末端连杆的空间姿态。将表1中各参数带入式(1)，求得Bi的坐标

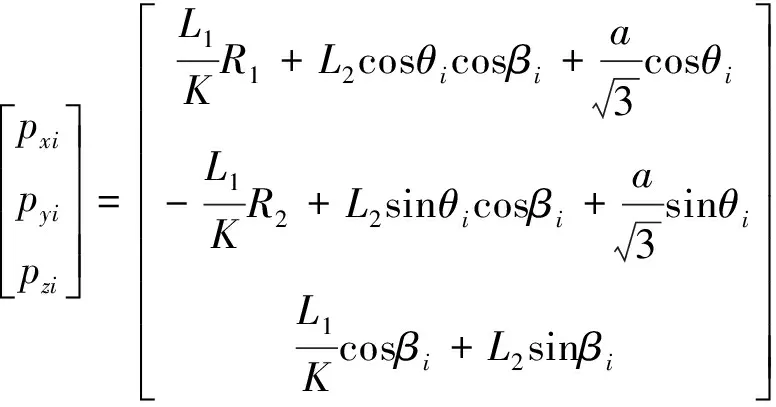
(2)

式中：

为了便于在编程中实现六维控制器对虚拟仿真的控制，采用Z-Y-X型动态欧拉角来描述上平台相对于参考坐标系的姿态。其中旋转矩阵R=[noa]，可通过3条支链末端球铰中心Bi的空间坐标值进行求解。各角的反正切表达式为

(3)

式中，

上平台中心O1点的坐标为

(4)

式(3)、式(4)即为并联机构位置正解，等号右边是用结构参数和关节变量表示的解析表达式来确定动平台的位姿。当给定各关节变量的变化范围时，便可求得3-URS并联机构的工作空间。

2.2 上连杆运动学正解

式(2)求得Bi的坐标即为上连杆的位置坐标。上连杆的姿态采用Z-Y-X型动态欧拉角进行描述。在齐次变换矩阵Ti中的旋转矩阵R=[noa]，其各单位方向矢量在参考坐标系上的分量为动坐标系各坐标轴的方向余弦。向量n、o、a的表达式分别如下：

式中：

L1=sinθitanαicosβi-cosθisinβi

L2=cosθitanαicosβi+sinθisinβi

R1=cosθicosβi

R2=sinθicosβi

Q=sinβicosβitanαi

上连杆Z-Y-X型动态欧拉角的反正切表达式为

(5)

式(2)、式(5)即为上连杆的空间姿态表达式。其空间位姿的正确性是3-URS并机构能否实现在虚拟环境中关联运动的关键。

3 MATLAB仿真实例

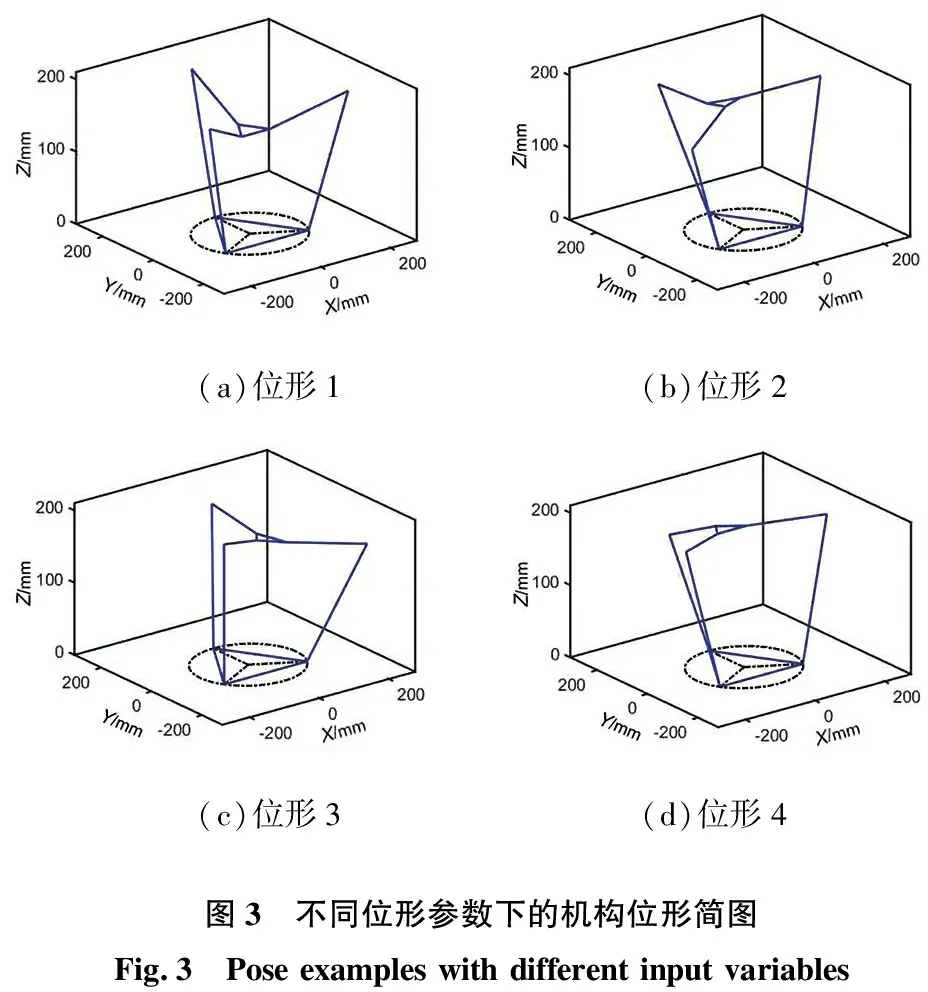
(a)位形1 (b)位形2 (c)位形3 (d)位形4图3 不同位形参数下的机构位形简图Fig.3 Pose examples with different input variables

表2 机构正解
Tab.2 Forward kinematic of the mechanism

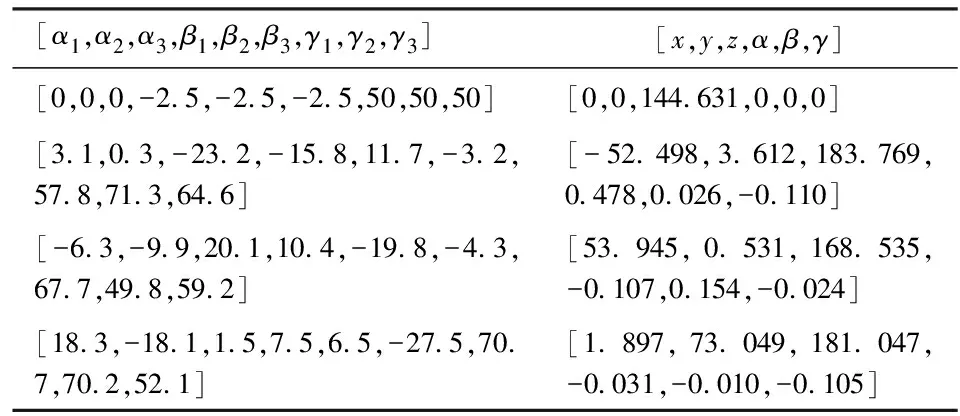
[α1,α2,α3,β1,β2,β3,γ1,γ2,γ3][x,y,z,α,β,γ][0,0,0,-2.5,-2.5,-2.5,50,50,50][0,0,144.631,0,0,0][3.1,0.3,-23.2,-15.8,11.7,-3.2,57.8,71.3,64.6][-52.498,3.612,183.769,0.478,0.026,-0.110][-6.3,-9.9,20.1,10.4,-19.8,-4.3,67.7,49.8,59.2][53.945,0.531,168.535,-0.107,0.154,-0.024][18.3,-18.1,1.5,7.5,6.5,-27.5,70.7,70.2,52.1][1.897,73.049,181.047,-0.031,-0.010,-0.105]

采用数值验证的方法来验证运动学正解的可靠性。根据运动学正解，求得动平台的位姿参数，然后将其与表3三维建模软件的标定值进行比较，结果表明误差均≤5×10-3。由此验证了3-URS并联机构运动学正解的正确性以及结构设计的合理性和可行性。

表3 机构位姿标定及误差
Tab.3 Error and pose calibration

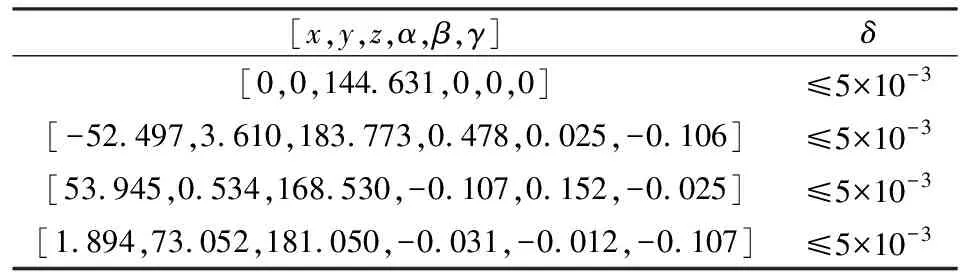
[x,y,z,α,β,γ]δ[0,0,144.631,0,0,0]≤5×10-3[-52.497,3.610,183.773,0.478,0.025,-0.106]≤5×10-3[53.945,0.534,168.530,-0.107,0.152,-0.025]≤5×10-3[1.894,73.052,181.050,-0.031,-0.012,-0.107]≤5×10-3

4 虚拟仿真系统

六维控制器的末端将外部受力与力矩直接和输出的位移增量和转动增量建立关系，然后再作用于各关联构件反推出其位姿。数据采集卡即时采集光电旋转编码器监测的各关节变量，在VS中利用DirectX技术把采集到的各关节变量，依据运动学正解模型进行处理，计算出各关联构件的空间位姿，实现3-URS并联机构在虚拟三维场景中关联运动并进行模拟仿真分析，控制系统流程如图4所示。

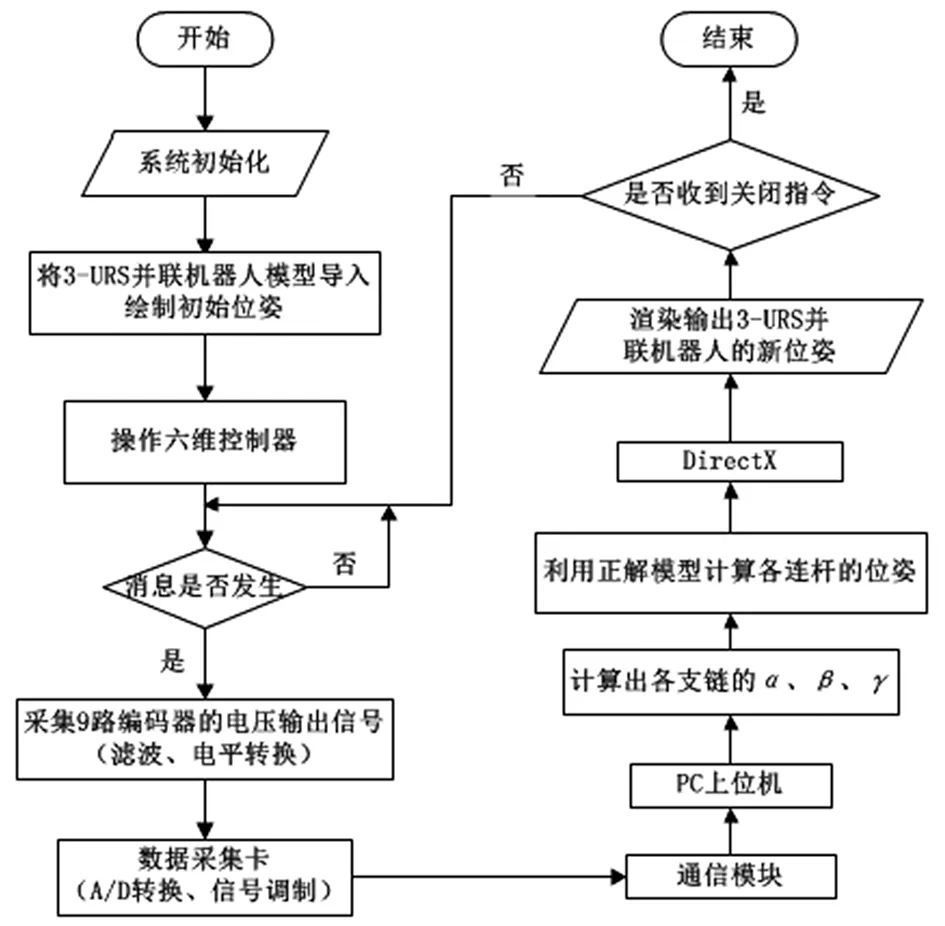
图4 控制系统流程图Fig.4 Flow chart of the control system

以上连杆为例进行介绍。根据各关节编码器所采集的关节变量，依据式(2)求得球铰中心Bi的坐标，依据式(5)求得上连杆的动态欧拉角。由于在DirectX中旋转变换是以世界坐标系进行变换，而求得的上连杆欧拉角是以其动坐标系进行变换。所以为了解决利用DirectX技术重绘上连杆的空间位姿问题，需要求得上连杆动坐标系在各次旋转变换中的空间位姿。这样就把绕上连杆动坐标系的旋转变换转换为绕世界坐标系中的特定轴的旋转变换。

点在左手直角坐标系中绕过原点任意轴r=(rx，ry，rz)旋转θ角的旋转变换矩阵为

Rot(r,θ)=

式中，

初始情况下，上连杆的动坐标系与世界坐标系完全重合。在世界坐标系的原点位置，依据上式旋转上连杆动坐标系的3个坐标轴，变换到所需的姿态后，平移到Bi点，再进行渲染操作。主要步骤如下：

(1)绕动坐标系的Z轴旋转α角。此时动坐标系的X轴和Y轴在世界坐标系下的矢量分别为[cosα -sinα 0]T、[sinα cosα 0]T。

(2)绕动坐标系的Y轴旋转β角。局部坐标系的X轴在世界坐标系下的矢量为[cosαcosβ-sinαcosβsinβ]T。

(3)绕动坐标系的X轴旋转γ角。此时得到的坐标系即所需的姿态坐标系。

在编程实现上连杆的姿态变化时，若中间旋转变换的过程采用四元数Q(x,y,z,w)=[sin(w/2)x, sin(w/2)y, sin(w/2)z, cos(w/2)](其中[x，y，z]为旋转轴，w为旋转角度)来表示坐标系的旋转变换，则可以有效避免物体在旋转变换的过程中出现欧拉角万向节死锁、矩阵数据处理量大、物体旋转变换出现不连续的问题。因为四元数具有不论刚体处于什么空间位姿都不会退化的优点，并且参数的范围不受限制，方程组线性化程度高，无奇异，只涉及代数运算，所以避免了大量三角函数运算。由四元数到旋转矩阵的变换公式为

Rot(r,θ)=

式中，

四元数将三维空间的旋转概念扩展到四维空间，这为表示和处理三维空间中点的旋转变换带来了极大方便。在程序中若广泛用四元数替换矩阵变换，不仅能节省内存资源，提高数据运算速度，同时也能降低计算处理成本。若需姿态变换矩阵，可依据上式把四元数转换成姿态变换矩阵。图5为3-URS并联机构虚拟仿真实例效果。

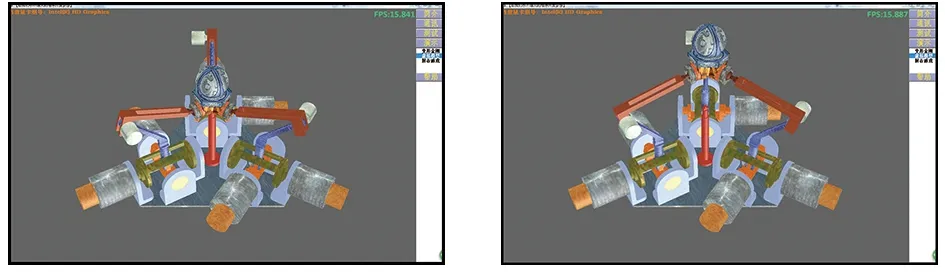
(a)效果1 (b)效果2

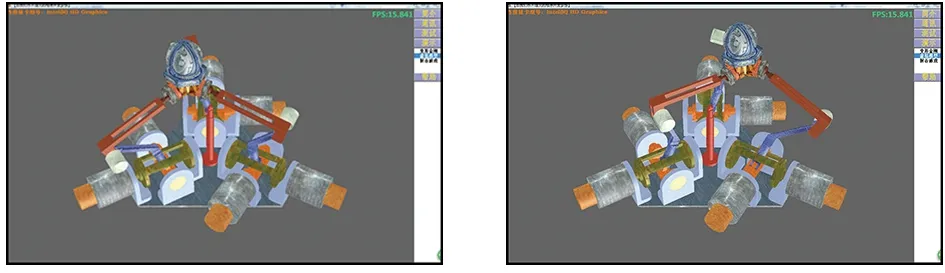
(c)效果3 (d)效果4图5 虚拟仿真系统运行效果图Fig.5 Results of the virtual simulation system

5 结论

1) 提出了一种基于宏动3-URS并联机构，利用光电旋转增量式编码器测量角位移的六维控制器设计方案。此并联机构利用3条完全相同且呈中心对称分布的URS支链，将静平台和动平台连接在一起，充分集成了并联机构、光电旋转增量式编码器、万向铰等的优点，为六维控制器的结构设计提供了一种新思路。

2) 已知六维控制器的各关节变量，对并联机构的正向运动学进行了封闭式完全耦合分析并利用MATLAB对数学模型进行了有效验证，从而为实时测量动平台的位姿提供了有力保证，同时也为虚拟环境中并联机器人的运动仿真分析提供了必要的理论依据。

3) 引入四元数表示坐标系旋转变换并进行正交规范化处理，基于DirectX技术构建了虚拟仿真系统，实现了六维控制器对虚拟机器人的实时控制，为机器人运动学验证提供了实时检测平台。