基于ARMA模型的粗糠醇精馏过程软测量建模方法

李隆浩，张立臻，马广磊

(1.中国石油大学(华东) 信息与控制工程学院,山东 青岛 266580； 2.山东新华医疗器械股份有限公司,山东 淄博 255000)

精馏塔是化工工业中常见的分离设备[1]，精馏过程是一个将组分复杂的混合物经过传热、传质分离成纯度相对较高的单一化工产品的过程，其原理是利用混合物各组分相对挥发度不同，在一定的温度与压力下通过蒸发和冷凝，使液相中轻组分与气相中的重组分相互转移，从而实现组分分离[2]。精馏过程是一个复杂而且庞大的过程，对精馏塔而言，它的特性除了受自身内部因素的影响之外，也受外部未知因素的影响，导致精馏过程存在动态时变性[3]，而且化工过程往往表现出显著的动态和延迟[4]，所以有必要建立精馏过程的软测量模型。为解决精馏过程软测量建模问题，文献[5]提出一种AddSVR模型，实现对醋酸共沸精馏中塔底醋酸组分的预测。文献[6]基于样本“代谢”原则，实现SVM增量学习。文献[7]基于PLS方法提出主曲线的软测量建模方法。文献[8]提出了一种基于小波核函数的极限学习机的软测量建模方法，并将其应用于醋酸精馏的软测量建模问题中。但是，上述方法均未考虑输入变量对输出变量的影响持续性问题，无法体现精馏过程的动态特性，导致软测量模型预测准确性低。

为将输入变量对输出变量的影响持续性融入软测量模型，提高软测量模型预测的精确性，本文提出一种基于ARMA模型的粗糠醇精馏过程软测量建模方法。

1 问题描述

粗糠醇精馏过程是时序流水线式生产过程，当前辅助变量的数值不仅对当前主导变量的数值产生影响，还会影响到后续主导变量的数值，即辅助变量数值对主导变量数值的影响具有持续性。

双塔精馏过程原理图如图1所示，图1中主导变量一般为精馏纯度，由3#成品罐采出。同时，在双塔精馏过程中， 由于液态粗糠醇的流转耗时以及物料存在一定程度的混合，导致辅助变量对主导变量的影响具有一定的持续性，且难以确定，导致软测量模型的预测准确性降低。

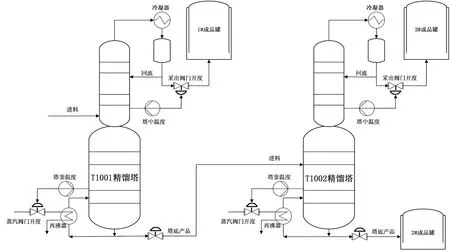
图1 双塔精馏过程原理图Fig.1 The working principle of a twin-column DP

2 软测量模型辅助变量的选择

针对图1所示粗糠醇精馏过程，根据现场实际调研，选择糠醇纯度作为软测量模型的主导变量，其常用软测量辅助变量见表1。

由表1可知，粗糠醇精馏过程一般有7个辅助变量，由于高维变量容易导致软测量模型出现病态，所以本文采用基于余弦相似度值的相关性分析方法对表1中的7个辅助变量与主导变量糠醇纯度进行相关性分析，找出影响程度最大的3个辅助变量，建立软测量模型。

表1 粗糠醇精馏过程辅助变量
Tab.1 Auxiliary variables in crude furfuryl alcohol distillation process

参数含义稳态值T1/℃T1001塔釜温度135T2/℃T1001塔中温度100L1/%T1001塔釜液位20～80F1/m3·h-1T1001塔中进料≤4T3/℃T1002塔釜温度125T4/℃T1002塔中温度120L2/%T1002塔釜液位20～80

余弦相似度计算公式为[9]

(1)

各辅助变量与主导变量的余弦相似度相关性数值见表2。

表2 辅助变量余弦相似度数值
Tab.2 Cosine similarity values of auxiliary variables

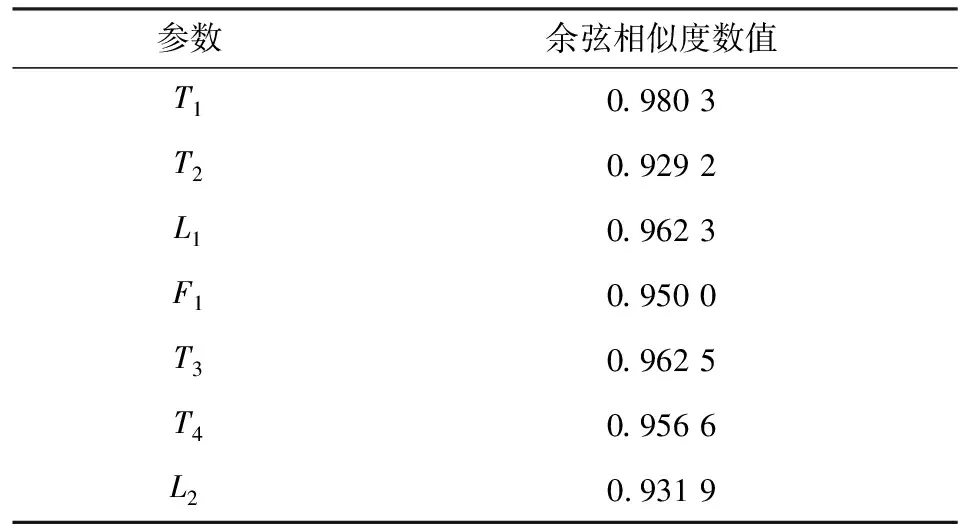
参数余弦相似度数值T10.980 3T20.929 2L10.962 3F10.950 0T30.962 5T40.956 6L20.931 9

通过分析表2中各辅助变量余弦相似度数值，选择T1001塔釜温度T1、T1001塔釜液位L1、T1002塔釜温度T3作为粗糠醇精馏过程软测量模型的建模辅助变量。

3 基于ARMA模型的粗糠醇精馏过程软测量建模方法

3.1 基于ARMA模型的软测量建模数据处理

粗糠醇精馏过程属于时序流水线式生产，辅助变量数值对主导变量数值的影响具有一定的持续性，虽然影响程度随着时间跨度的增大而减小，但是影响程度数值难以确定。针对上述问题，本文提出一种基于ARMA模型的粗糠醇精馏过程软测量建模方法。

常规ARMA(p,q)模型如下[10]：

(2)

式中：p,q为该模型的阶数；φ为AR的阶数p的运算符；θ为MA的阶数q的运算符。

本文采用的多点输入ARMA模型如图2所示[11]。

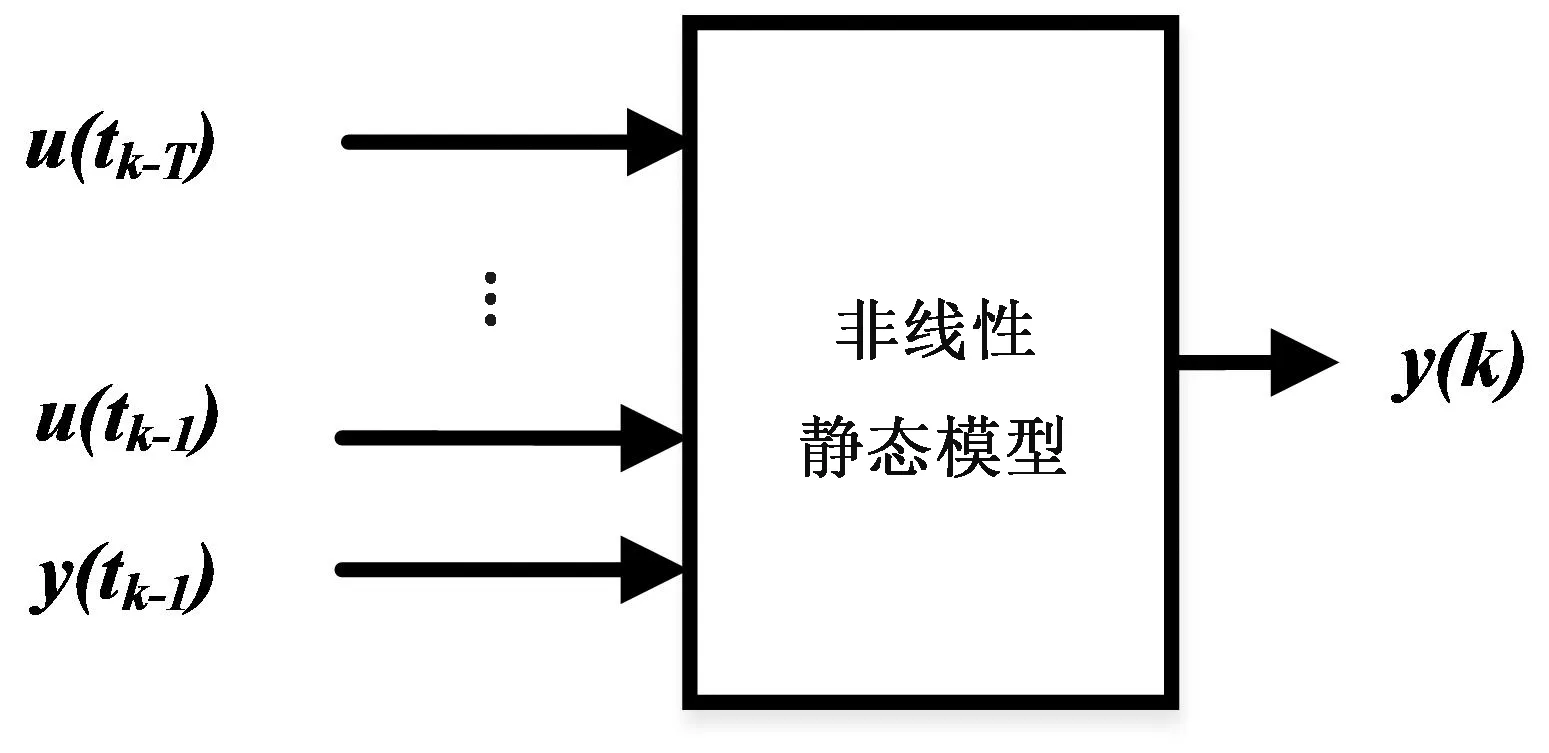
图2 多点输入ARMA模型结构图Fig.2 ARMA model structure with multipoint input

其广义函数表达式为

y(k)=f(X(k),θ)

(3)

X(k)=[u(tk-1),…,u(tk-T),y(tk-1)]

(4)

得到软测量建模样本数据集为

(5)

将上批次的输出作为有效输入加入建模辅助变量样本数据集，可以融入时间跨度较大的辅助变量数值对当前批次主导变量数值的影响，有效提高软测量模型的预测准确性。

3.2 基于LSSVM的软测量建模

最小二乘支持向量回归机是由Suykens等[12]提出解决函数估计问题的机器学习方法，具有更好的收敛精度，更适用于粗糠醇精馏过程小样本数据软测量建模。

LSSVM模型为[13]

y(x)=ωTφ(x)+b

(6)

目标函数为

(7)

约束条件为

yi=ωTφ(xi)+b+ξi(i=1,2,…,l)

(8)

通过KKT条件，得到用于函数估计的LSSVM模型，即

(9)

本文选择径向基核函数

(10)

则通过建模数据样本集S建立了粗糠醇精馏过程的软测量模型。

4 粗糠醇精馏过程仿真实验及结果分析

4.1 粗糠醇精馏过程仿真实验

本文的粗糠醇精馏过程数据来自工业现场，按时间顺序排列，共包含152组可用数据，选择前100组数据作为模型训练数据，后52组数据作为模型测试数据。所有样本数据均进行归一化处理。

基于ARMA模型的软测量建模采用如下模型结构：

(11)

由于平均绝对误差(MAE)、均方根误差(RMSE)在评价软测量模型的拟合程度及数据预测准确性的普适性，本文选用MAE及RMSE作为模型的拟合程度及数据预测的准确性的评价指标。

(12)

(13)

LSSVM参数为：C=80、σ2=3。

LSSVM方法与ARMA-LSSVM的模型数据训练曲线图如图3所示。模型训练评价指标数值见表3。

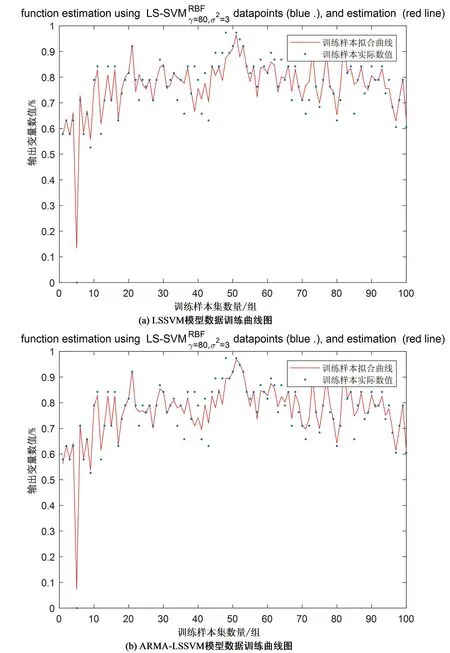
图3 模型训练曲线对比图Fig.3 Contrast chart of model training curve

表3 模型训练性能评价指标数值
Tab.3 Evaluation index value of model training performance

建模方法MAE/%RMSE/%LSSVM0.064 90.093 0ARMA-LSSVM0.051 60.073 7

LSSVM方法与ARMA-LSSVM的模型数据预测曲线图如图4所示。模型预测评价指标数值见表4。

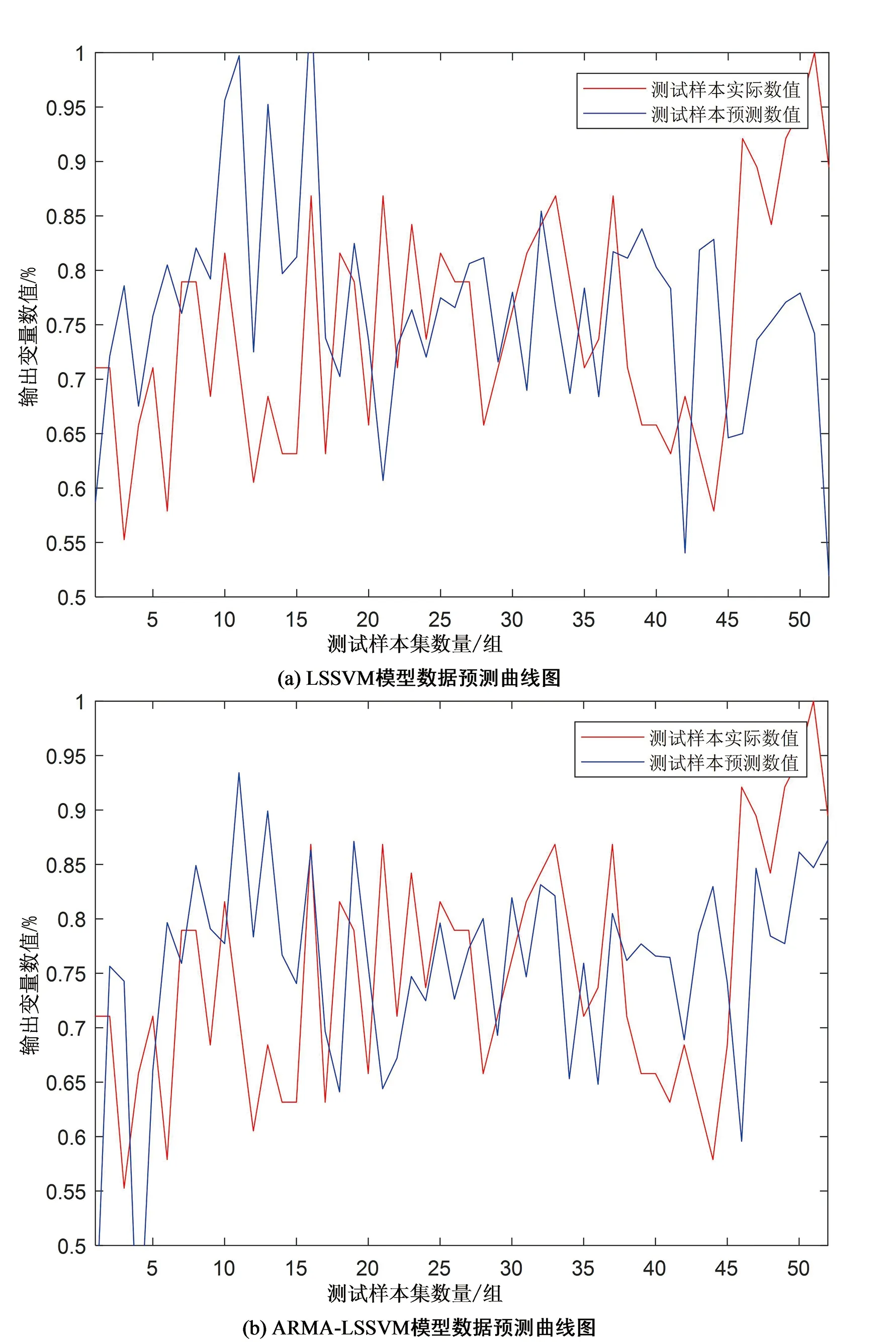
图4 模型预测曲线对比图Fig.4 Contrast chart of model prediction curve

表4 模型预测性能评价指标数值
Tab.4 Evaluation index value of model prediction performance

建模方法MAE/%RMSE/%LSSVM0.124 00.152 8ARMA-LSSVM0.111 10.139 4

4.2 结果分析

本文基于粗糠醇精馏过程的实际数据对所提出的LSSVM方法与ARMA-LSSVM方法进行仿真建模对比分析。

由于本文的仿真实验均基于工业过程实际数据，存在较大的噪声，所以导致训练及预测曲线均出现较大的偏移。

对比图3(a)与图3(b)中LSSVM方法与ARMA-LSSVM方法的训练曲线发现，基于ARMA-LSSVM方法的软测量模型训练曲线更能贴近实际数值，结合表3中MAE、RMSE评价指标数值可知，ARMA-LSSVM方法的模型训练拟合程度与LSSVM方法相比，MAE值提升了20.49%，RMSE值提升了20.75%，证明基于ARMA-LSSVM方法训练出的软测量模型在拟合性能上是优于LSSVM方法的。

对比图4(a)与图4(b)中LSSVM方法与ARMA-LSSVM方法的预测曲线发现，基于ARMA-LSSVM方法的软测量模型预测曲线偏移量较少，结合表4中MAE、RMSE评价指标数值可知，ARMA-LSSVM方法的模型训练准确性与LSSVM方法相比，MAE值提升了10.4%，RMSE值提升了8.77%，证明基于ARMA-LSSVM方法训练出的软测量模型在预测性能上是优于LSSVM方法的。

5 结束语

本文以粗糠醇精馏过程为研究背景，通过对粗糠醇精馏过程实际数据的仿真建模研究表明，本文提出的基于ARMA模型的粗糠醇精馏过程软测量建模方法，可以有效提高软测量模型的拟合程度和数据预测准确性。虽然在拟合效果及预测准确性上具有一定的提升，但是效果依然不好，究其原因是由于工业现场实际数据噪声较多，而且LSSVM方法参数也对拟合性能及预测准确性产生了一定的影响。