尺规作图教学用力点在哪儿
——由尺规作图的作业批阅说起
2019-11-13江苏省苏州市胥江实验中学校
江苏省苏州市胥江实验中学校 蒋 凯
一、由尺规作图的作业批阅说起
八年级上学期初学全等三角形、轴对称、线段垂直平分线之后,学生都会使用尺规作图进行一些基本作图,如角的平分线、线段的垂直平分线等.但是阶段检测时,往往都会考查以下一个经典的尺规作图问题(见图1),根据教学经验,总有一些学生不能得到这个题目的满分.很大比例的学生只是画对角平分线,但线段垂直平分线的作图不正确(见图1).

图1
线段的垂直平分线是基本作图之一,教师上课时都会组织学生学习并教授作图方法.然而,从批阅反馈情况来看,恐怕关于尺规作图的作图教学是“低效”的.
二、尺规作图的教学用力点在哪儿
1.教师要先安排学生分析作图条件
作图之前需要先安排学生认真分析题意,想清问题的条件与作图的目标与方向,然后画出示意图进一步分析作图的可能性,以及作图之后图形具有哪些特征,需要运用哪些几何性质.在此基础上,再构思作图的步骤与先后次序,然后初步规划作图方案,并利用限定的作图工具开展作图.如果教师缺少上述让学生充分审题的教学环节,则学生往往就是被动模仿操作步骤,对问题的本质不甚清楚,难以达到深刻理解的程度,也缺少了审题教学这个前置环节.
2.教师要重视示范并教授作图步骤
在审题之后,学生基本想清了草图示意,规划了作图流程,这时教师要重视亲自示范并教授作图步骤,而不能以播放PPT来代替操作示范.当前,教育信息化、现代化装备不断更新升级,有些教室黑板的功能几乎都被电子屏取代,有些教师甚至一节课都不进行板书,只是在PPT或电子屏上进行一些演算、标注,然后一屏接一屏往下翻,学生难以形成整节课板书的整体结构之感,重要的板书内容、作图痕迹、作法依据,应该一直保留在黑板的显著位置,让学生能长时间关注,形成较强的视觉印象,促进他们深刻理解.
3.作图之后需要引导学生进行证明
作图之后,不能急于开展同类练习,以大量练习来训练学生作法的熟练程度,而应该通过“拉长”对经典问题的理解时间来实现深刻理解这类问题.比如,尺规作图之后,要引导学生进行证明,证明时需要调动已有知识、经验进行推理论证,可以想清辨明作法背后的依据,体会几何作图的操作可能与步步有据.而且在证明之后,还可以促进学生对相关几何定理的关联理解,使学生知道数学知识的前后一致与逻辑严谨.也可以这样说,单独一道尺规作图题仅是一道习题,但如果要求学生把作图问题作为一个项目来研究,包括审题、作图、证明、下结论,这样就经历了一个完整的项目化研究.
想起一道经典的选择题,如图2,是作角平分线的尺规作图及痕迹,画图依据主要体现了全等三角形的哪一个判断依据?
根据教学经验,很多学生都会错选为“SAS”.
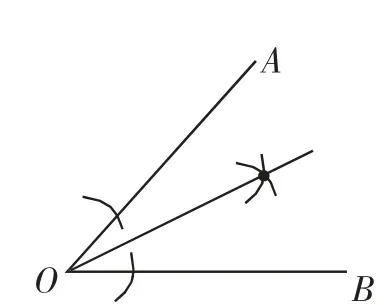
图2
三、对“掐头去尾,只烧中段”尺规作图教学的进一步反思
尺规作图是经典平面几何问题,历史悠久、博大精深.初中阶段只是涉及一些基本作图及初步运用,并不提倡探究一些较难的尺规作图问题.下面略做一些梳理,并针对“掐头去尾,只烧中段”式的作图教学提出一些反思和建议.
案例1:作线段的“和、差、倍”
这种作图题常常给一条线段或两条线段,然后求作一条新的线段,新线段与已知线段是和、差或倍数关系.教学时如果直接示范教授作法,让学生模仿作图步骤,而不说清道理,就是典型的“烧中段”教法.完整的教学,可以先引导学生分析待作的线段与已知线段有什么关系,再安排学生画出草图分析,然后拟定可行的画图步骤,想清顺序,再下手作图,作图之后要结合图形标注恰当字母,进行简单的示意与推理说明.
案例2:已知底边及底边上高的长求作等腰三角形
给定底边及底边上的高的长(也就是两条线段的长),要求作出符合要求的等腰三角形,这是一个经典尺规作图问题.如果直接给出(复制)一条线段(假设为底边),然后作出它的垂直平分线,进一步,在垂直平分线上截取出高的长,最后写出三角形为所求,这是典型的“烧中段”教法.完整的教学,先引导学生分析问题的条件(即题设),然后画草图分析:需要满足什么条件?如何实现?作图的顺序怎样确定?哪些步骤涉及了基本的尺规作图?这些都应该在动手作图之前有清楚的思考,然后就“了然于胸”,有条不紊,渐次作图.作图之后,写出结语,继续给出证明,由作图出发利用线段垂直平分线的性质,证明所作三角形有两边相等,从而确认所作三角形是符合要求的等腰三角形.如果班级学生整体水平较高,还可进行变式拓展,引导学生思考和挑战:
变式拓展题:已知两条线段的长(长度不等),求作等腰三角形,使腰长为较长线段,一腰上的高为较短线段的长.
教学组织:安排学生先经历画草图分析,构思作法,实施作法,这里初步涉及了所谓“奠基三角形”的思路,并且可以与全等三角形判定方法(“斜边、直角”即HL法)进行关联理解.当然,这道拓展作图题,最大的问题在于漏解,因为满足条件的三角形并不唯一,对于培养学生思维的严谨性也有很好的训练价值.在此基础上,还可跟进一道学生以前做过的易错题.
同类练习:已知等腰三角形一腰上的高与腰的夹角为50°,求该等腰三角形顶角的度数.
案例3:作三角形的外接圆与内切圆
九年级学习圆的内容之后,三角形的外接圆、内切圆的概念就陆续出来了.这时尺规作图作出一个三角形的外接圆、内切圆就是学生应该掌握的.实际教学进程中,不少学生往往停留在简单模仿层面,能画出一个三角形的外接圆,但并不知道或不深究其中的“简化”作图的道理.比如,作出一个三角形的外接圆,只需要作出三角形任意两条边的垂直平分线,以它们的交点为圆心,该圆心到三角形任意一个顶点的距离作为半径画圆即可,三角形的外接圆作好之后,还需要进行证明,为什么此时三角形三个顶点恰在同一个圆上?也就是尺规作图的第三个教学环节,作图之后的证明环节必不可少.而这种证明又可以与八年级学生初学全等三角形后,所学习的角平分线的性质与判定定理进行有效关联,体会数学内容的前后一致、逻辑严谨.类似的,三角形内切圆的作图教学也有这样的特点,只要作出两条内角平分线的交点(即三角形内心),再过内心向边作垂线段,该垂线段的长即为内切圆的半径,从而可实现成功作圆.接着安排学生进行证明,关联理解八年级时所学过的命题“求证三角形三条内角平分线交于一点”.
四、写在后面
教学即研究,一线教师在繁重的日常教学工作中如何摆脱“西西弗斯推巨石上山”的繁杂无趣呢?也许把日常教学工作中的“手头小事”都当成教学研究的素材来思考、研究,就是一种防范职业倦怠的有效方法.事实上,面对一些经典问题,学生掌握的效果不好,更多的情况应该是反思我们的教学方式与教学方法,而不是埋怨学情,因为很有可能是教师非常熟悉经典问题的处理流程,却忽略了学生的最近发展区,想当然地认为学生也应该很熟悉这些经典问题.想来,这也就是章建跃先生倡导的“理解学生”的重要涵义吧.
