关注解题训练，培养思维品质

甘肃省天水市麦积区龙园中学 吴金凤

作为数学教学中最基础的一项学习活动，解题是学生初步形成数学思维的重要一步，是磨砺思维品质的重要组成部分.在传统教育观念中，解题也就是解答习题，如模仿性习题、实际问题和开发题等多种问题.当然，学生探究数学问题的过程也是发展优良思维品质的过程.所谓优良思维品质，主要包括思维的发散性、敏捷性、创造性、严谨性.思维品质不是教师“教”的，也不是学生“学”的，而是通过不断的解题训练自然形成的.

一、重视观察训练，培养观察能力

观察是引领学生获取感性认知的途径，也是学生实现思维加工的基础.无论是把握数据之间的关联还是识别图形的特征，又或是发现隐藏的基础规律，都离不开细致入微的观察.培养学生的观察能力更是提升学习品质和提高教学效率的有效途径.

例1请观察以下式子，…（ab≠0），其中第7个式子为______.

分析：首先，整体观察题目，得出这些式子的分母中都含有a，分子中都含有b，不同之处在于每个式子的符号、分母和分子的指数；接着，深入观察这些式子的不同之处，可以看出每个式子的符号呈现负、正交替的形态，可以用（-1）n（n为正整数）来表示，分母的指数呈现1、2、3、…的规律，可以用an表示，分子的指数呈现2、5、8、11、…（每个指数间隔3）的规律，可以用b3n-1表示.最后，第7个式子，即分母的指数为7，即n=7时，式子为

二、强化联想训练，培养创造性思维

联想，是一个人生来便具有的天赋.但是，作为一种创新能力，还需要后天加以训练和发展，联想的能力越强，就越能将意义不同的事物相关联，找寻其中蕴含的规律性的东西，架起沟通的桥梁，有意识地用联系的眼光看待两部分的内容，丰富自身解决问题的策略，提高解决问题的能力，最终提升数学学科素养.因此，在解题中需要不断强化联想训练，培养创造性思维.

例2如图1所示，OA=OB=OC，且∠ACB=30°，那么∠AOB=（ ）.

A.70° B.60° C.50° D.40°

分析：从OA=OB=OC这一条件展开联想，可以想象到“圆为到定点距离等于定长的点的集合”，现以点O为圆心，边OA为半径作圆（如图2），⊙O经过A、B、C三点，运用“相同弧所对的圆心角等于所对圆周角的两倍”便可求出∠AOB的度数.

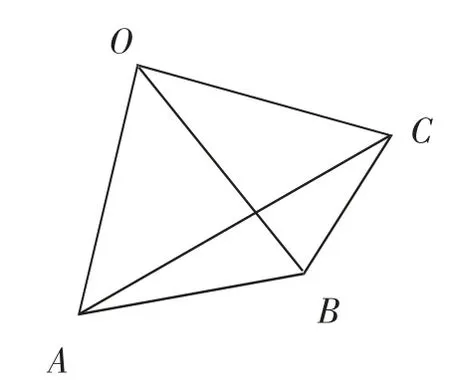
图1

图2

例3如图3所示，点P位于等边△ABC内，现有PC=5，PA=3，PB=4，请求出∠APB的度数.

分析：这道题的难度比较大，我们可以由其中的一个条件出发联想出构造性问题，则可以将难度降低.现在观察三边的长度，并展开完整的联想，在线段与勾股数之间建构桥梁，联系到直角三角形.然后，通过变换图形将PA、PB、PC三条线段集中到一个三角形中，问题就可以迎刃而解了.

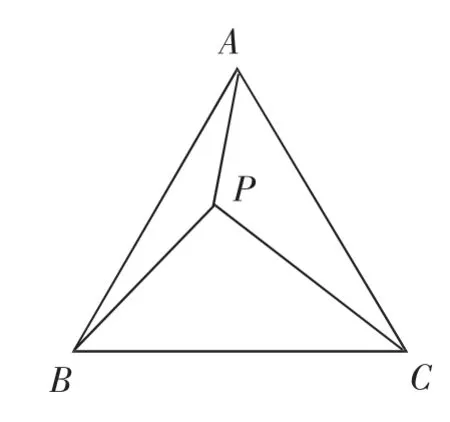
图3

图4

解：如图4，将△BAP绕点B沿顺时针方向旋转，当旋转至60°时，BA、BC重合，点P旋转至点Q，连接PQ.

∠PBQ=60°，BP=BQ，则△BPQ为等边三角形，则PQ=PB=4.又PC=5，CQ=4，则在△PQC中，PQ2+QC2=PC2，则△PQC为直角三角形，则∠BQC=60°+90°=150°，则∠APB=150°.

三、关注特值法，培养思维的捷性

用特值法解题具有从特殊到一般的认识规律，可以培养新时代学生快速反应的基本素质，提高思维的敏捷性.作为数学教师，训练学生用特值法解题，既可以帮助学生快速解决一些选择题和填空题，还可以培养学生的数学感觉，提高他们的探究、猜想、发现等整体素质.

例4如果实数x、y、z不全相等，a=x2-yz，b=y2-xz，c=z2-xy，则以下结论正确的是（ ）.

A.a、b、c都不大于0

B.a、b、c都不小于0

C.a、b、c中至少有一个大于0

D.a、b、c中至少有一个小于0

分析：根据条件可得x、y、z为不全相等的实数，那么可以分为以下两种情况：①x、y、z各不相等，②x、y、z中有两个是相等的.若x、y、z各不相等，我们可以假设x=1，y=0，z=-1，即可得出a、b、c都等于1，这样一来A和D选项就可以排除掉了；若x、y、z中有两个相等，我们可以假设x=0，y=1，z=1，即可得出a=-1，b=1，c=1，同样排除掉B选项.综上所述，此题选C.若此题运用一般解法解决，过程复杂，不少学生下手有困难，若分析条件和结论，并为字母赋予特殊值，则很容易快速获取准确答案，有利于学生快速反应能力的提升.

例5如果函数y=的自变量x的值是实数，则k的取值范围为（ ）.

A.k≥1 B.k＜0或k＞1 C.0＜k≤1 D.0≤k≤1

分析：根据条件可得k=0满足题意，而观察选项，只有D中包含0，因此此题选D.此题运用一般解法过程烦琐，不免费时费力，特殊值法是除繁就简的思维方法之一，可以起到事半功倍的奇效.

四、着眼解题过程的逻辑化，培养严谨性思维

现今的数学教学中，由于大量的例题讲解和习题训练，不少教师在讲解时只注重解题思路的叙述，忽略了解题过程的严谨性，它带来了重结论轻过程的负面影响.学生在解答时，把复杂的解题过程浓缩为几个简单的字母、数或字，出现了过程上的漏洞百出.长此以往，导致学生不重视解题过程的严谨规范，出现了解题过程书写凌乱、逻辑性紊乱的现象.因此，在数学教学中，需重视训练学生解题过程的逻辑性，从而培养学生思维的严谨性.

例如，在运用“一元二次方程的根的判别式”解决问题时，如果二次项系数包含字母，则教师必须重申“二次项系数不可为0”这一前提条件，杜绝学生在完成选择或填空题时由于这一前提遗漏而产生各种错误.

五、多题一解，培养综合归纳的思维方式

所谓多题一解，就是学生通过相同的知识点进行多个练习，经过梳理、归纳和提炼揭开各种习题的表层，探索其知识的本质，实现数学知识应用的发展性，培养学生一种综合归纳的思维方式.

例6如图5所示，在△ABC中，有AB=6，AC=8，点D为边BC的中点，求AD的取值范围.

分析：此例题中只需要将边AD延长至点E，使DE=AD，可得，再加上三角形的三边关系，可得1＜AD＜7.

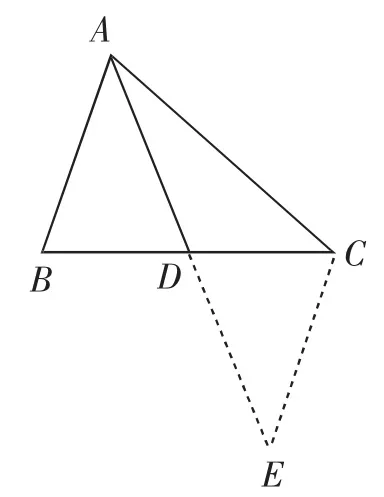
图5

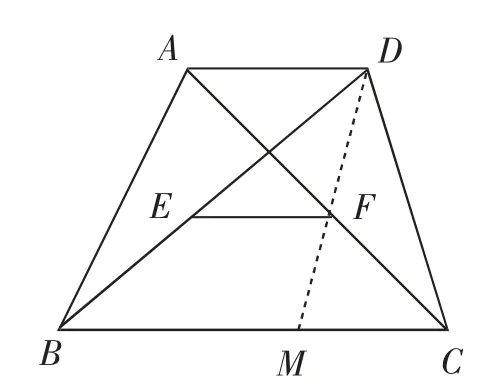
图6

例7如图6所示，已知梯形ABCD，有AD∥BC，AD＜BC，点E为对角线BD的中点，点F为对角线AC的中点.求证：EF=

分析：此例题中，连接DF，并延长与边BC相交于点M，可得再加上三角形的中位线性质即可求证.

由此可见，此类问题的解决尽管表现形式不同，但问题本质意义相同，在解完一题后让学生进行总结归纳，适时地将解题经验实现发散性迁移，从而获取熟练的解题技巧.

六、一题多变，培养学生思维的发散性

一题多变是通过纵横发散，使知识串联、综合、沟通，培养学生的发散思维，对培养创新人才具有重大意义.

例8已知一次函数y=（2m+4）x+（3-n），当____时，此函数为正比例函数.

变式1：已知一次函数y=（2m+4）x+（3-n），当____时，此函数的图像经过第一、二、三象限.

变式2：已知一次函数y=（2m+4）x+（3-n），当_____时，此函数的图像不经过第四象限.

变式3：已知一次函数y=（2m+4）x+（3-n），当_____时，此函数的图像与y轴的交点位于x轴下方.

变式4：已知一次函数y=（2m+4）x+（3-n），若此函数的图像是由直线y=2x-4向上平移5个单位所得的，那么m=____，n=____.

变式5：已知一次函数y=（2m+4）x+（3-n），当____时，该图像与直线y=2x-4关于x轴对称.

变式6：已知一次函数y=（2m+4）x+（3-n），若该函数的图像与函数y=的图像相交于点（1，2）、（-2，-1），那么不等式的解集为________.

一个简单的一次函数问题，通过结构不停变换来巩固学生对知识的掌握并让学生灵活运用，以培养学生的创新精神和思维的发散性.

总之，在初中数学解题教学中，教师应善于利用各种方法培养学生的思维品质.这不仅可以让学生的思维品质得到快速成长，还可以从根本上激发学生的数学兴趣，培养学生自主学习的能力，提高学生的数学水平，提升教师的教学质量.