数学课堂中几个常见“遗憾”的剖析和反思

浙江省宁波市第七中学 姚力娇

动态生成的课堂是真实的，体现的是新课程的理念，但随之出现的是教师无法预料的情况，难免会带着或多或少的遗憾.不过，作为新课改背景下的教师，我们无需苛求完美无缺的课堂，但需学会关注、捕捉和反思每一节课中的遗憾，并努力找寻方法弥补和改进，让数学课堂更灵动、更优化.那么，我们如何不断反思和改进教学中的缺失现象呢？本文中，笔者选取具有典型意义和探究价值的教学片段或一些实施环节进行案例分析，反思课堂中常见的教学遗憾.

一、教师过度让位的“遗憾”

新课改风向标下，师生的角色也发生了重大改革，学生的主体地位越发凸显，“以生为本”已成为教学的一种习惯.这样一来，不少教师便会片面地认为，无论是什么教学内容，不管是什么教学目标，放权给学生，让学生亲历知识的形成便是对学生主体地位的一种肯定.学生的主体地位放大化，教师转变成教学过程中的一个旁观者，这种过度让位的现象实际上是对学生主体的一种放任自流，教学效果也是可想而知的.

案例1：以“直线和圆的位置关系”（第2课时）的教学片段为例.

首先，教师以“任务串”的形式快速导入课堂：翻开教材并仔细阅读第38至39页除练习以外的内容，并独立完成活动单，然后小组合作交流，最后分组展示，比一比哪个小组的学习更有效.学生快速投入到自主学习中，仔细研读教材，不少学生能准确圈出概念中的关键字词；一个个都能认真思考活动单上的问题并一一解决，最终一个解决问题让大部分学生“卡壳”了.

例题：如图1所示，OM为∠AOB的角平分线，点P是OM上一点，现以点P为圆心作⊙P，⊙P和OA相切，且切点为D.求证：⊙P与OB也相切.

事实上，教师很快便发现了学生的“卡壳”现象，但他并没有施以援手或引导学生小组合作讨论，大概是不想过早介入，不想给予学生过多的牵制.

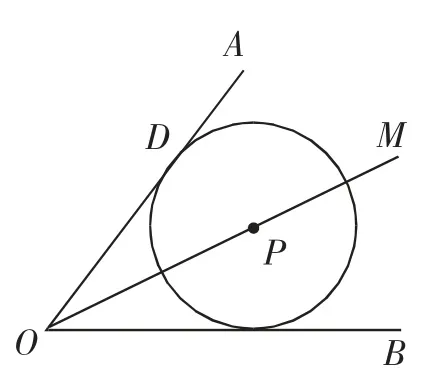
图1

随着时间的流逝，学生再也按捺不住，展开了一番讨论……教师仅仅是这组听听，那组看看，整个过程保持沉默，似乎仅仅是实施课堂教学的“监控”.展示环节有条不紊地开始了，终于轮到了这道让大多数学生困惑不已的题了.此时距离下课仅剩6分钟.

生1：我认为点P作为∠AOB的角平分线上一点，可以过点P作OA和OB的垂线……

生2：你这样是错的，应该连接点P和点D，不然的话过点P作OA的垂线不和点D重合吗？

师：还有其他不同意见吗？

此时，教师显然有些着急了.他这里想呈现的结论是：若题设中呈现了直线与圆的公共点，则“连接半径，证明垂直”即可；若题设中未呈现直线与圆的公共点，那么就需“作垂直，并证半径”.

不过，此刻学生面面相觑、满脸疑惑，无法作答.

反思：此案例中学生自主学习、合作交流的过程一览无遗，充分体现了学生的主体地位.但是，学生对于切线三种判定方法掌握了几分？会添加辅助线吗？此处的数学本质仅凭学生阅读教材是无法领悟的，这些必须由教师以“问题链”进行引导，由学生展开辩论方可实现.

可以在原有教学过程的基础上改一改，牢牢把握学生“迫切生成”的时机，由以下一系列“问题链”为指引，引导学生在分析和辩论中突破教材中的难点，并落实重点：

（1）如图2所示，直线l是否为⊙O的切线？

让学生清楚不能依靠直观判断，判定方法之一是定义法，需明示直线与圆有唯一的公共点.

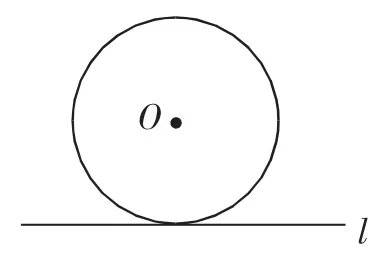
图2

（2）若⊙O的直径是10cm，点O到直线l的距离是5cm，那么直线l是否为⊙O的切线？

让学生清楚判定方法之二“d=r法”，可以通过计算来判定.

（3）如图3所示，已知⊙O上有一点A，过点A的直线l和半径OA在满足什么条件时，可证明直线l为⊙O的切线？这种判定法与“d=r法”有何区别？

对判定法进一步巩固，让学生清楚这里所用的定理就是从推理角度判定的“d=r法”.

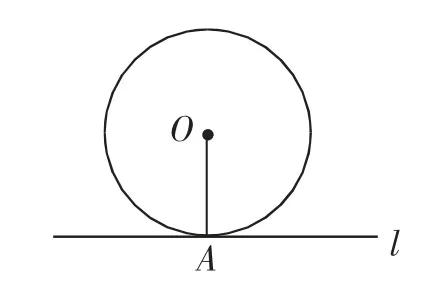
图3

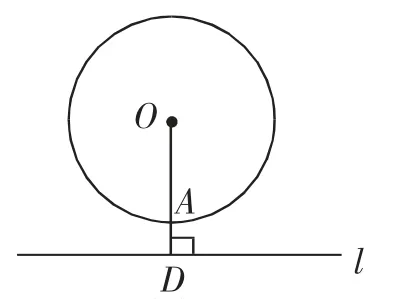
图4

（4）如图4所示，过圆心的直线OD与⊙O相交于点A，且直线OD垂直于直线l，现将直线l向上平移，当平移到哪个位置时，直线OD和⊙O第一次相切？

让学生清楚此题的本质也是判定法“d=r法”.

（5）分析用切线判定定理证明某直线为圆的切线存在几种情况，并思考与之对应的证明策略是什么.

总结归纳出案例中教师尝试呈现的结论.

教材是引领学生认知发展和建构知识的“中介”，也就是说，教材是实施教学的范例，是师生之间交往互动的平台.这就要求教师主动设计和开发教材，从“教”教材转变为“用”教材，将教材中的知识本质提炼出来，生成自身的数学思考，促进学生的发展.同时，在教学过程中，教师应当智慧地开展教学，关注学情，以学定教，及时给予学生点拨和诱导，创造性地开展教学，让课堂成为自主学习的课堂，而非放任自流的课堂.

二、浅显数学理解的“遗憾”

专家与一线教师一致认为，新课程改革的三大基石为理解数学、理解学生、理解教学.然而现实教学中，相当一部分教师在第一基石方面存在着一定的遗憾，自身对数学理解浅显，导致教学浅显，教学效果自然是低效的.

案例2：以“待定系数法求一次函数解析式”的教学片段为例.

教师用“直入式”揭题后引导学生阅读教材，并回到以下问题：

（1）什么是待定系数法？

（2）运用待定系数法求一次函数的解析式有哪些步骤？

（3）分析例题，尝试解决以下问题.

（4）在问题解决的过程中，需注意哪些问题？

本章节的知识与方法都呈现单一化的特点，再加以例题的辅助，更适宜通过学生自学来完成教学过程，并可以较为高效地完成教学任务.

反思：思考并反思教学过程，在案例的教学过程中，似乎存在着一些遗憾.比如，观察表1并写出y与x之间的函数关系式：

表1

学生可以正确填写这个表格吗？答案是不确定.此案例中，学生的学习过程仅仅是学习的第一阶段“模仿”，对“用待定系数法求一次函数解析式”的认识不够深刻.笔者认为，需从以下三个方面进行渗透：

第一，需让学生明确函数的类别.教师需将例题中出示的“一次”略去，采用引导学生合作讨论的方式，使学生对这里的函数解析式有一个清楚的认识.

第二，需让学生明确函数的一般表达式.即使前一个课时中已然借助生活实例充分概括，但此课中仍需进行不断强化和巩固.

第三，需让学生明白待定系数的个数与序数对的个数应当一致.笔者认为，本课的教学重点之一为“变式中活用待定系数法求一次函数解析式”.我们可以借助文字型、图像型、表格型的题目，去设置开放题，让学生在富有“数学味”的课堂中厘清重、难点，充分开发学生的潜能，创设高效数学课堂.

总之，在教学中，伴随着教学的深入，学生会生成各种想法和质疑.教师则需依据学生的具体情况厘清思想脉络，观察学生的思维走向，并随时随地地调整教学策略，让学生成为课堂的主人.教师还需充分理解数学，引导学生去实践、思考、探究、交流等，获得数学的基础知识、基本技能、基本思想、基本活动经验，促进学生积极主动、富有个性地学习.当然，带有遗憾的课堂才是真正灵动的课堂，但我们需厘清遗憾所在，并不断找寻策略调整和弥补，让遗憾不断成熟我们的课堂，让师生共同在遗憾中成长.