“基本模型”引领下的教学设计与思考——以初中几何相似中A字、Z字模型为例

陈思宇

南京师范大学附属中学新城初级中学，江苏 南京 210019

初中数学；基本模型；教学设计；思考

教学过程

一、教学目标

理解A字、Z字型模型和反A字、Z字模型的基本概念，并能在与相似有关的图形中识别此基本模型。

能利用此基本模型对相似有关问题进行证明或求解。

能在复杂图形中抽象出此基本模型，并在此基础上对复杂的问题进行证明和应用。

二、教学重难点

重点：理解A字、Z字型模型和反A字、Z字模型的基本概念，并能识别基本模型及证明三角形的相似。

难点：能在复杂图形中抽象出此基本模型，并对复杂的问题进行证明和应用。

三、教学流程

（一）认识模型

1.追根溯源

如图1，在相似三角形的证明过程中，常常出现由平行线所产生的A字、Z字型的基本模型。苏科版九上教材P54通过证明亦得到如下结论：平行于三角形一边的直线与其他两边相交，所截得的三角形与原三角形相似。

2.探索变式

问题1：如何证明图1中A字、Z字型模型的△ABC∽△ADE？

问题2：将图1进行怎样变换也会得到∠1＝∠2？此时会出现相似三角形吗？请证明。

设计意图：教材是中考的源头，也是初三复习必须回归的起点，此基本模型由书本上的平行线所得到的A字型基本模型出发，引申出Z字型及反A字、Z字型模型，完全从课本出发，体现了“源于教材，高于教材”的用心，并积极地“溯源登高”。同时，设计问题1和问题2，回归教学的本质，以学生为主体，教师为引导，以探究为主线，研究此基本模型在相似中的证明和应用。

（二）典型例题

例1.如图3，△ABC中，∠A＝70°，AB＝4，AC＝6，

将△ABC沿图中的虚线剪开，则剪下的三角形与原三角形不相似的是（ ）。

图3

例2.如图4，AB、CD相交于点O，OC＝2，OD＝3，AC∥BD，EF是△ODB的中位线，且EF＝2，求AC的长。

设计意图：例1瞄准教学目标，具有一定的基础性，充分体现了这几种模型，目的在于让学生清楚地识别，认清几种基本模型的特点。例2选自一道中考题，从平行线出发，融合了A字、Z字型两种模型，稍加综合，符合学生的认知规律，既体现了这一模型的重要性，它是中考常考的重点之一，又能进一步理解和认识这一模型，并用此模型为解题提供一定的方法和思路。

（三）巩固练习

1.如图5，若∠B＝∠C，则__________∽__________，理由是__________，且__________∽__________，理由是__________。

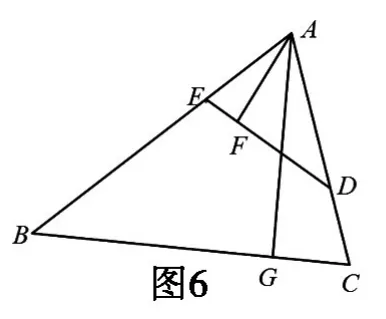
2.如图6，在锐角三角形ABC中，点D、E分别在边AC、AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF＝∠GAC．求证：△ADE∽△ABC。

3.如图7，在△ABC中，AC＝8cm，BC＝16cm，点P从点A出发，沿着AC边向点C以1cm/s的速度运动，点Q从点C出发，沿着CB边向点B以2cm/s的速度运动，如果P与Q同时出发，用t（秒）表示移动的时间（0≤t≤8），那么，当t为何值时，△PQC与△ABC相似？

设计意图：三道练习题选题精准，突出重难点和教学目标，主要从三角形的角度出发，研究了A字、Z字型、反A字型等模型，多选自中考题，既涉及到基本定理的阐述、相似的证明，又有动点问题引起的分类讨论，题型较典型，覆盖面广，符合学生的实际情况，从同学们的反馈情况来看，绝大多数同学都能根据基本模型迅速解题，具有练习的意义和价值。

（四）拓展提升

如图8，已知AD是△ABC的角平分线，☉O经过A、B、D三点。过点B作BE∥AD，交☉O于点E，连接ED。

（1）求证：ED∥AC；

（2）若BD＝2CD，设△EBD的面积为S1，△ADC的面积为S2，且S12－16S2＋4＝0，求△ABC的面积。

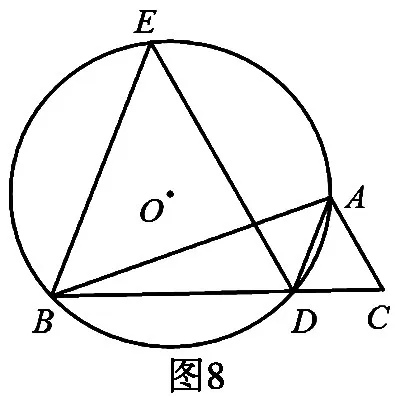
设计意图：此题涉及到圆的相关知识，具有一定的难度，综合性较强，主要为攻克难点准备，表面上看不出使用相似，但如果引导学生看到图中Z字型的基本相似模型，就会在计算面积的时候合理利用好相似，从而使问题得以解决，可以供学有余力的学生尝试一下。

（五）作业与小结

四、教学反思

（一）选材既要紧扣模型，又要注重真、小、实

以“基本模型”为专题的复习课，所选题型必须紧扣此模型，这样才能让学生找到其共同特点和解决办法，同时又要根据学生的实际学习情况选择切口小、问题真、针对性强的题型，不求面面俱到，而是要结合复习的目标要求，针对学生的薄弱环节，力求解决学生的真问题。本节课选择的是几何中常见的A字、Z字型基本模型，切口比较小，覆盖面也基本在圆和相似这两章的内容。其次，此模型是相似中的常见模型，针对性非常强，学生若能掌握好这种基本几何模型，对于他们学习相似，乃至学习其他几何问题，提高解题和思维能力都大有裨益。最后，从学生的真实情况出发，A字、Z字型模型在相似中的应用是中考的常考问题之一，部分学生在学习时还不能举一反三、融会贯通，因此，非常有必要选择这一模型开设中考专题复习课。

（二）例题突出典型问题，充分体现模型本质

“基本模型”复习课的例题选择不用全面宽泛，而是应当具有一定的针对性和代表性，充分体现模型的本质，立足解决学生认知结构的真问题。例1题目比较基础，考察的点也很单一，并不复杂全面，但非常具有代表性，充分体现了此模型的本质，学生若能辨析好例1，对于后面认识和利用此模型解决较复杂的问题就非常得心应手。例2选自一道中考题，题目并不复杂，但很典型，学生在解决这一问题时，既利用此模型举一反三、触类旁通，又能注意到这是中考常考的重点之一，准确把握好中考的方向，提高复习效率。

（三）习题设计串起一类，利用模型融会贯通

“基本模型”的习题设计，可以从一些考察单一知识点的问题入手，不用处处设计综合性较强的问题，而要力求找到一条主线，串起一些零散的问题，并能够揭示这些问题之间的内在逻辑关联，使所复习的知识整体化和系统化。以巩固练习中的3道练习题为例，题目并不复杂，而且每一题所考察的知识点都比较单一，但是它们中都存在A字、Z字型、反A字型等模型，这些基本模型将这些问题串联起来，帮助学生找到解决这一类问题的基本方法，使得学生在以后的学习中可以解决同类型的问题，从而达到举一反三的目的。从课后作业的完成情况来看，同学们基本上都顺利地完成了基本题型，可见对于此模型掌握已达到基本要求，后面还设计了几个难度较大的题目，目的在于让学有余力的学生进行探究，同时也是对这一模型的进一步挖掘。

（四）还课堂于学生，让精彩不断生成

课堂教学是预设和生成的有机融合，预设是为了更好的生成，“基本模型”复习课的教学中，更要给学生足够的思考时间，让学生回顾和梳理问题解答的过程，体会它们之间的本质联系。本节课从开始提出模型就给出了学生探究的时间，接着例题由学生寻找模型，并总结经验和方法，还有学生提出他自己的技巧，巩固练习也多由学生自行解决，这样，学生在心里串起了一条主线，也渐渐发现这类问题的特点，于是就润物细无声般生成了解决此类问题的一般思想方法，而不是在单个题目的具体解法上，“基本模型”的目标就此达成。

以上是笔者对“基本模型”在初三复习课教学中的一些实践和思考，“基本模型”教学条理清楚不零散，结构简洁有深度，如何进一步利用“基本模型”来提高课堂效率和学习效率，笔者还将在今后的实践中不断地探讨与改进。