一道关于抛物线的高考试题的多向探究*

(宁德市高级中学,福建 宁德 352000)

例1已知抛物线C：x2=-2py经过点(2,-1).

1)求抛物线C的方程及其准线方程；

2)设O为原点，过抛物线C的焦点作斜率不为0的直线l交抛物线C于点M,N,直线y=-1分别交直线OM,ON于点A,B,求证：以AB为直径的圆经过y轴上的两个定点.

(2019年北京市数学高考理科试题第18题)

本题的答案是：1)抛物线C的方程为x2=-4y,准线方程为y=1；2)以AB为直径的圆经过y轴上的两个定点(0,1)和(0,-3).其中第2)小题的内涵丰富，意境深邃，笔者引导学生进行了一系列的探究.

1 探究一般性

问题1由第2)小题的结论你能猜想出一般性的结论吗？

显然，在第2)小题中，直线y=-1为抛物线C通径所在的直线，定点(0,1)恰为抛物线C的准线与对称轴的交点，不妨称之为“准点”，而定点(0,-3)恰为“准点”关于焦点的对称点，由此不难猜想一般的情形：

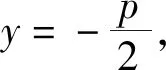
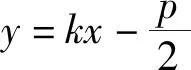
整理得

x2+2pkx-p2=0.

x1+x2=-2pk,x1x2=-p2,

易求得直线OM,ON的方程分别为

即

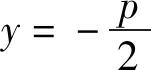
线段AB中点的横坐标为

进而可得以AB为直径的圆的方程为

令x=0,得

即

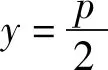
可见猜想1成立,即：

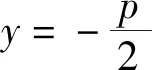
2 探究综合性

问题2以上结论揭示了抛物线C：x2=-2py(其中p>0)的特有性质，那么对于抛物线x2=2py(其中p>0),y2=-2px(其中p>0)和y2=2px(其中p>0)，有什么类似的结论？

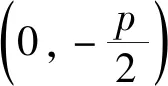
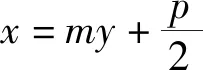
整理得

y2-2pmy-p2=0.

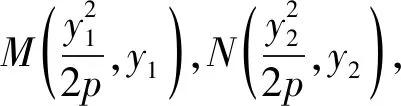
y1+y2=2pm,y1y2=-p2，

易求得直线OM,ON的方程分别为

即

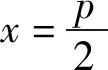
线段AB中点的纵坐标为

进而可得以AB为直径的圆的方程为

令y=0,得

即

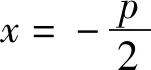
分别仿照探究1和探究2可证得抛物线C：x2=2py(其中p>0)及y2=-2px(其中p>0)的情形,猜想2成立,由此可把探究1的结论及猜想2的结论综合为:

性质1设过抛物线C的焦点作不与对称轴平行或垂直的直线l交抛物线C于点M,N,点O为抛物线C的顶点，通径所在的直线分别交直线OM,ON于点A，B，则以AB为直径的圆经过该抛物线C的“准点”及其关于焦点的对称点.

3 探究变式

问题3以上性质揭示了抛物线顶点、焦点弦(不垂直于对称轴)与通径所在直线之间的内在联系，如果把通径所在的直线换为抛物线的准线，那么它们之间会有什么样的内在联系？

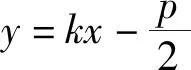
x1+x2=-2pk,x1x2=-p2,

直线OM,ON的方程分别为

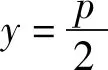
线段AB中点的横坐标为

进而可得以AB为直径的圆的方程为

令x=0,得

即

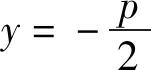
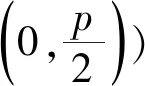
性质2设过抛物线C的焦点作不与对称轴平行或垂直的直线l交抛物线C于点M,N,点O为抛物线C的顶点，准线分别交直线OM,ON于点A，B，则以AB为直径的圆经过该抛物线的焦点及其关于“准点”的对称点.

4 探究推广

问题4性质1和性质2分别揭示了抛物线顶点、焦点弦(不垂直于对称轴)分别与通径所在的直线、准线之间的内在联系，如果把顶点O推广为抛物线上的任意一点P，那么以AB为直径的圆能否经过某两个定点？

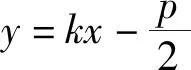
x1+x2=-2pk,x1x2=-p2,

又直线PM的斜率为

进而得到直线PM的方程为

同理可得直线PN的方程为

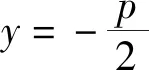
又以AB为直径的圆的方程为

即

为求该圆与y轴的交点坐标，可令x=0，得

显然，仅当xAxB为负常数时，此方程才有两个实数解，即该圆与y轴交于两个定点.而

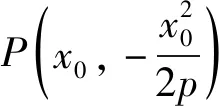
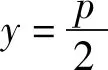
可见，无法把性质1中的顶点O推广为抛物线上的任意一点P，性质1的推广失败.

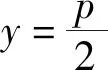
这时以AB为直径的圆的方程为

即

当x=0时，上述方程为

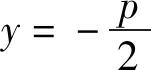
显然，这两个定点恰为抛物线C的焦点及其关于“准点”的对称点，即把顶点O推广为抛物线上的任意一点P，性质2的结论不变.类似地，对于其他类型的抛物线，也有相同的结论.

性质3设过抛物线C的焦点作不与对称轴平行或垂直的直线l交抛物线C于点M,N,点P为抛物线C上的任意一点，准线分别交直线PM,PN于点A,B，则以AB为直径的圆经过该抛物线的焦点及其关于“准点”的对称点.

特别地，当抛物线C的方程为y2=4x,点P为H(1,2)时，以AB为直径的圆经过抛物线C的焦点F(1,0)及关于“准点”(-1,0)的对称点(-3,0).这就是:

例2已知点F(1,0),直线l：x=-1，直线l*⊥l于点P，线段PF的垂直平分线交l*于点Q.

1)求点Q的轨迹C的方程；

2)已知点H(1,2),过点F且与x轴不垂直的直线交C于点M,N，直线MH,NH分别交l于点A,B，求证:以AB为直径的圆必过定点.

(2017年福建省普通高中毕业班单科质量检查文科数学试题第20题)

本题或许是上述高考试题的源头吧！根据性质3，上述试题中的点“H(1,2)”可以放宽为“轨迹C(即抛物线y2=4x)上的一点H”，因为这并不改变原来的答案.

以上关于抛物线的性质能否推广到椭圆、双曲线的情形，可以引导学生继续探究.限于篇幅，本文从略.

以上通过对一道高考试题的多向探究，得到了抛物线的顶点、焦点弦与通径所在直线的关联性质及其变式和推广，揭示了问题的本质和规律，使学生经历了在教师指导下的“问题—猜想—探究—结论”的“再创造”过程，亲身体验和品尝探究的曲折和成功的喜悦.这无疑有助于学生对圆锥曲线问题的深度学习，更重要的是有助于培养和提升学生的探究能力和数学学科核心素养.这正如《普通高中数学课程标准(2017年版)》所指出：在教学活动中，应结合教学任务及其蕴含的数学学科核心素养设计合适的情境和问题，引导学生用数学的眼光观察现象、发现问题，使用恰当的数学语言描述问题，用数学的思想、方法解决问题.在问题解决的过程中，理解数学内容的本质，促进学生数学学科核心素养的形成和发展.