一种同时满足攻击角度和时间的航迹规划方法*

姚冬冬，王晓芳，田 震

(北京理工大学宇航学院， 北京 100081)

0 引言

随着战争向信息化发展，单枚导弹作战模式已很难满足当前复杂的作战任务需求，多导弹协同作战成为导弹作战的新趋势[1]。如果多枚导弹能够在同一时刻从不同方向攻击目标，则能大大提高导弹的突防能力和对目标的打击能力[2]。航迹规划是实现这一复杂协同作战任务的核心，因此，研究同时具有攻击时间和攻击角度约束的协同航迹规划方法具有重要的意义[3]。

针对具有攻击角度约束的航迹规划问题，文献[4-5]提出了一种由目标出发并反向搜索获得控制点的方法，实现了攻击角度的约束。对于多飞行器飞行时间协同的问题，文献[6-7]基于期望航迹长度改进了代价函数，获得了与期望距离相差较小的航迹。文献[8]同时考虑了攻击时间和攻击角度约束，设计了多导弹协同航迹。但仍存在计算方式复杂、人为因素较多、搜索效率较低等不足。

对于多飞行器之间避免碰撞问题，文献[9]通过设置节点之间安全距离的方式，保证了航迹规划中的飞行安全。但这种方式约束性过强，会使协同航迹搜索区域变小，并给攻击角度的实现带来困难。文献[10]则提出了一种基于Voronoi图的可交叉航迹规划。

稀疏A*算法(SAS)作为一种高效的启发式算法，因为其解具有全局最优性，被广泛应用在航迹规划领域和矿井搜索、灾区救援等场合[11-13]。

文中同时考虑多导弹攻击时间和攻击角度的约束，基于SAS算法设计了能够躲避环境威胁、避免弹间碰撞且从指定方向同时攻击目标的航迹，并对航迹进行了平滑处理。通过仿真验证了算法的有效性。

1 满足攻击角度约束的单弹航迹规划

1.1 A*算法和SAS算法基本原理

A*算法是一种经典的启发式搜索算法。从起点开始进行节点扩展，将每个可行节点进行代价赋值，选取全局代价最小的一点继续搜索直至目标点，其代价函数为

f(n)=g(n)+h(n)

(1)

式中：n表示当前节点，g(n)表示在状态空间中从起始节点到当前节点的实际代价值，h(n)表示从当前节点到目标节点的估计代价值，称为启发函数。

SAS算法是在A*算法的基础上的一种改进算法。保持代价函数形式不变，将飞行器的机动约束和任务约束加入到搜索算法中，对搜索空间进行了精简，提高了搜索效率。一般的，算法有两点变化。

1)搜索方式。增加了如飞行最短航迹段、最小转弯角等约束，将节点扩展方式从“九宫格”搜索变为扇面搜索，如图1所示。

图1 搜索方式变化

2)航迹的收敛。在A*搜索下，地图被栅格化，目标被设置在某一栅格内。而当前节点与每一个扩展节点都相邻，因此航迹一定会收敛到目标点。而在稀疏A*搜索下，搜索空间经过修剪，目标位置不一定能够恰好与扩展节点重合，因此要设定相应的搜索结束条件。对于导弹攻击目标的情况，则要求航迹最终到达目标点。

1.2 基于飞行约束和轨迹光滑的节点扩展

在节点扩展时考虑飞行器的约束是稀疏A*算法的一个基本步骤。根据几何关系和飞行约束有

(2)

式中:v为导弹运动速度，nmax为可用过载，g为重力加速度，dmin为最小航迹长度，表示导弹在改变姿态时必须直飞的距离，φmax为最大转弯角。

为了得到可飞航迹，需要对航迹段进行平滑处理。假设导弹在转弯处按照可用过载飞行，那么得到的平滑航迹将会是一段圆弧。为了实现连续的两段转弯，搜索的步长dmin至少为最小航迹长度的两倍，如图2所示。

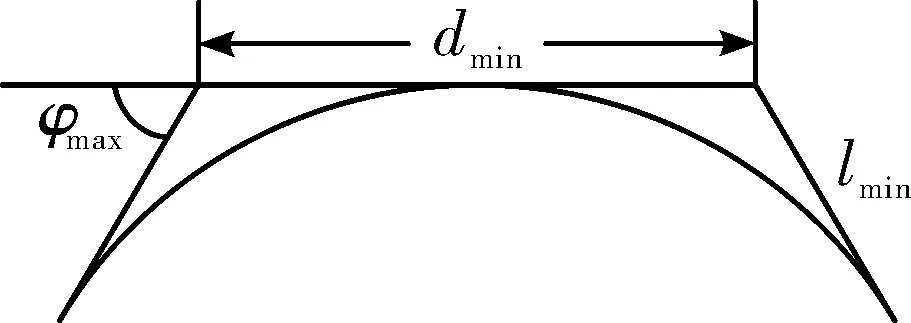
图2 步长选取示意

1.3 具有攻击角度约束的航迹规划方法

文中采用单控制点下改进代价函数的搜索方式，高效快速地满足了航迹的攻击角度约束。

导弹以指定角度攻击目标的示意图如图3。图中，T为目标点，θd为期望攻击角度，Δφ为进入目标方向角范围，当没有控制点时，Δφ是一个很小的范围。图3(a)表示单纯角度约束，这种方式程序上实现比较容易，但是效率很低、时间长。为解决此问题，加入了单控制点来实现攻击角度约束。

控制点选取方式如图3(b)所示，以目标T初始点，按照攻击角度反向延伸一个步长d的距离，得到控制点C。将得到的控制点作为新的目标点。这样，既扩大了收敛时角度约束，提高搜索效率，又满足了角度约束。根据文献[4]，过多控制点会降低搜索效率，文中只选取单控制点。

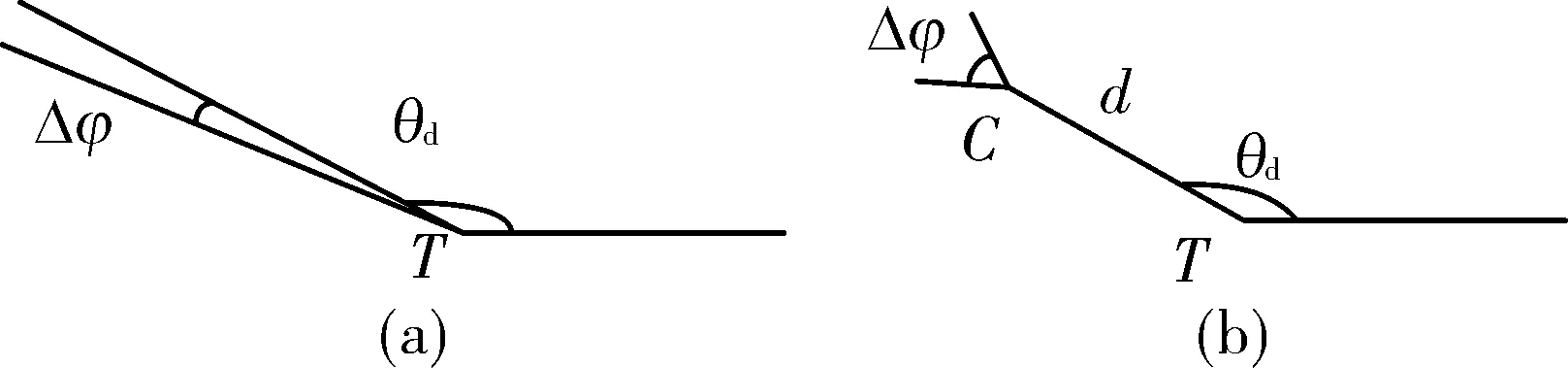
图3 角度约束方式

改进代价函数方式如下：代价函数f(n)中，实际代价值g(n)保持不变,而启发函数h(n)则同时考虑预估长度代价和预估角度代价，其表达式为：

(3)

式中:l为当前节点到目标点直线距离，θ表示当前航迹段航向角度，l*、θ*分别为归一化参考数值。

2 多弹协同航迹规划方法

多弹协同航迹是指：每个导弹在满足自身约束的单条航迹基础上，生成的满足协同约束的多条航迹。文中的协同约束包括攻击时间、攻击角度和弹间避碰。通过上一节，可以得到具有攻击角度约束的单条航迹，本节则实现了同时满足攻击时间、攻击角度和避碰约束的航迹协同。

2.1 时间协同方式

假设各枚导弹运动速度相同且保持不变，那么时间协同的问题可以对应为航迹长度协同的问题。先通过前文提出的航迹规划方式获得每一条导弹的路径；考虑最短航迹无法再进行缩短，选取其中最长的一条作为参考航迹并获得期望长度ld；然后对其它航迹重新进行顺序规划，最终得到同时满足角度和时间约束的协同航迹。

通过改进代价函数来实现长度协同。为了同时满足角度和长度要求，将代价函数f(n)分为角度代价和航程代价两个部分，其表达式为:

(4)

2.2 节点扩展过程中的碰撞检测与避碰

在协同航迹扩展过程中，必须考虑弹间的避撞。令航迹不交叉是一种常见的处理方式[9]，这种方式实现容易且具有较好的避撞效果。但在实际情况中，航迹不交叉的约束性较强，会减小搜索空间。事实上，即使航迹交叉，两枚导弹不同时到达交叉点，也不会发生碰撞。基于这种情况，同时考虑时空因素，对碰撞进行检测。

文中的避撞方案为：在进行节点扩展时，若当前航迹段与已有航迹相交，两条航迹到达交点的时间间隔应大于设定的安全时间间隔，即Δt≤|t1-t2|；若时间间隔小于Δt，则舍弃该段航迹。这样就实现了航迹之间时空上的避撞。由于导弹速度不变，安全时间间隔可以等效为安全距离Δl。

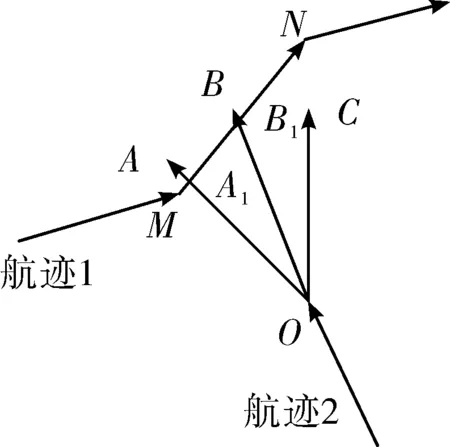
图4 航迹碰撞检测

2.3 算法流程

整个算法流程如下：

1)初始化算法参数；

2)求出每条航迹的攻击角度控制点，根据式(3)修改代价函数；

3)搜索得到具有攻击角度约束的多条航迹；

4)选取其中最长一条得到其他航迹参考长度；

5)根据式(4)修改代价函数，并在节点扩展中加入碰撞检测与躲避措施；

6)依次搜索得到同时满足攻击角度和攻击时间的多条协同航迹。

3 仿真分析

仿真在MATLAB环境下进行。4枚导弹协同攻击固定目标，目标的位置为(0 km,15 km)，4枚导弹的初始位置、发射角以及设定的理想攻击角度如表1所示。导弹速度均为300 m/s，可用过载为5。

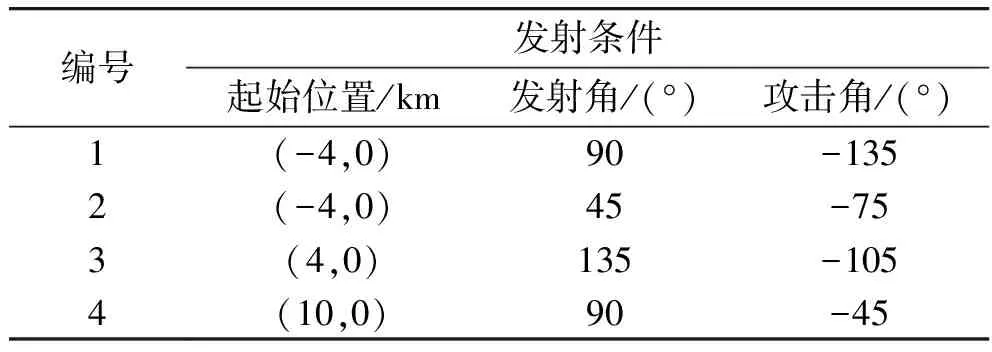
表1 导弹发射条件

根据节点扩展规律，取步长为0.6 km，转弯角为18°，每步扩展3个节点。设安全距离为0.3 km，对应安全时间间隔为1 s。

假设战场中有5个威胁，并将其等效为圆模型，威胁布局如表2。

表2 威胁位置

采用具有攻击角度约束的航迹规划方法，得到4枚导弹的航迹如图5所示。

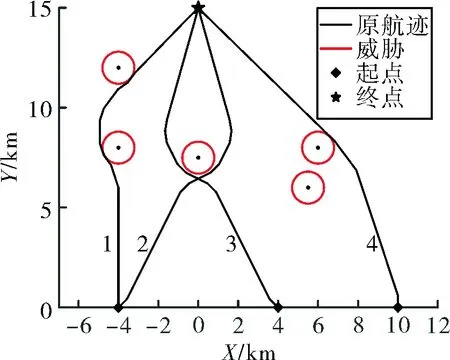
图5 具有攻击角度约束的4枚导弹航迹

由仿真结果可知，每枚弹都能够按照要求的攻击角度击中目标，达到了角度上的协同。每一条航迹都是在满足角度约束下，能够完成躲避威胁的最短航迹。这4枚导弹对应的航迹长度分别为17.142 km、17.184 km、17.184 km和18.575 km。最长和最短航迹相差了1.43 km，对应时间约为4.8 s，显然无法达到时间协同的效果。与此同时，第2、3条航迹交于(0,6.44 km)这一点，且到达时间都是在出发后的第21.7 s，明显这两条航迹是不安全的。

根据文中使用的时间协同方式，选取最长的一条(第4条)航迹作为参考航迹，采用修改后的代价函数和节点时空避撞扩展方法再次进行航迹规划，得到结果如图6。

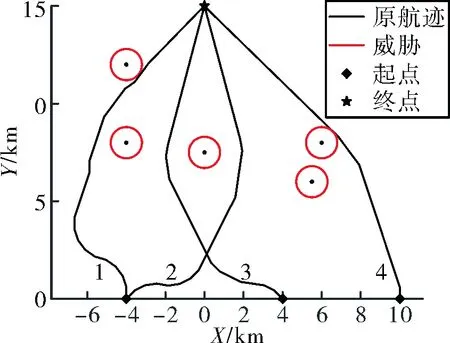
图6 时间和角度协同航迹

对比图5和图6可以看出，为了达到长度上的协同，前3枚弹会在航迹规划的初期适当地绕行以扩展航迹长度。最终这4条航迹的长度分别为，18.495 km、18.465 km、18.465 km、18.575 km，最长和最短航迹相差0.11 km，对应时间约为0.367 s。在一定误差范围内可以认为实现了时间上的协同。再关注航迹交叉点，第2、3条航迹交于点(0.33 km,1.43 km)，导弹2从起始点到交叉点的距离为4.89 km，导弹3从起始点到交叉点的距离为4.16 km，空间上相差了0.73 km，时间上相差了2 s，满足飞行安全要求，实现了航迹之间的避撞效果。

最后对航迹段进行平滑处理，得到可飞行航迹如图7。在航迹转弯处，用圆弧代替折线段使轨迹平滑。轨迹平滑对航迹长度改变很小，可以忽略其对整个长度的影响。同时，安全时间间隔的设置也避免了其对碰撞时间产生的影响。仿真结果表明该算法能够有效地获得满足角度和时间约束航迹。

图7 平滑轨迹

4 结论

文中基于稀疏A*算法提出一种多导弹在飞行过程中能够满足躲避威胁区、避免弹间碰撞、攻击末端角度和攻击时间要求的协同航迹规划方法。首先通过增加单控制点和改进代价函数相结合的方法获得了满足攻击角度约束的航迹。然后，假设导弹速度相同，将攻击时间等效为航迹长度，选取多枚导弹满足角度约束航迹中最长的航迹作为参考航迹，重新设置其他导弹的代价函数并进行搜索，在搜索过程中进行多弹航迹的时空安全性判断与重置处理，最终得到同时满足攻击时间和攻击角度约束且能避免弹间碰撞的多导弹协同航迹。最后，将得到的折线航迹进行平滑处理，进一步得到了多导弹可飞航迹。该方法为多导弹的协同飞行提供了较强的技术支撑。