旋转弹二维弹道修正组件修正能力影响因素仿真分析*

柯知非，高 敏，王 毅，惠江海

(陆军工程大学， 石家庄 050003)

0 引言

对于旋转稳定的炮弹而言，其转速可至万转每分钟，在此转速下无法进行弹道的修正。针对该情况，若要实现弹丸在射程与侧偏上的二维修正，可采用弹道修正组件代替传统引信。修正组件通过引入隔旋机构，使前体组件与后体弹体形成二体差旋运动，组件相对地面减至较低速的旋转，再利用控制舵的偏转来改变全弹所受气动力，进而调整弹体姿态以实现弹道的二维修正。

弹道修正是为了降低弹丸的散布，提高弹丸的命中精度，因而对其修正能力也有着较高的要求。由于修正组件是利用舵的升力来修正弹丸弹道，所以在减小弹道散布的同时也不可避免的带来了射程的损耗。为使修正弹在满足稳定性要求的同时，获得更大的修正能力，国内外的相关学者主要就旋转稳定弹丸的气动特性进行了研究。

S. Je等采用CFD仿真计算的方法获得了0.6～2.5Ma、固定舵舵偏-10°～10°弹丸的气动参数，目的在于验证风洞实验的实验数据[1]。经对比发现，计算的气动参数具有10%的误差。郝永平团队、汪亚利研究不同固定舵结构参数对弹丸气动特性的影响，并得到以下结论：若舵片形状和舵偏角相同，舵片面积越大，所提供的升力和阻力越大；若舵片形状和面积相同，舵偏角越大，弹丸的升力越大，而阻力的增加并不明显；面积和舵偏角相同的舵片，展弦比越大升力越大[2-5]。纪秀玲等利用TVD格式求解N-S方程，采用双时间推进方法对带可旋转固定鸭舵的旋转弹丸的流场进行数值模拟，分析其俯仰特性随鸭舵方位角的变化规律，并指出同一马赫数下全弹的法向力系数和俯仰力矩系数随俯仰角呈可用三角函数拟合的周期性变化[6]。吴萍研究了舵片旋转与不旋转条件下气动参数的变化，指出：超音速条件下，旋转弹丸阻力系数在2Ma时相比不旋弹丸较小，但随马赫数的增大两者差距逐渐减小；而升力系数和俯仰力矩系数基本不变；马格努斯力系数和马格努斯力矩系数在相同攻角的条件下随马赫数的变化曲线相同[7]。

通过以上分析可知，国内外对不同结构参数时弹丸的气动参数有了较为充分的计算分析，也得出了一些共性的规律。但以上的研究仅为体现影响修正能力的内因，未体现修正控制策略与外界条件的影响。赵万江等研究了海拔高度对一维修正弹修正能力的影响，得出的结论是，在4 500 m海拔条件下的弹丸射程修正量明显小于在0 m海拔下的修正量，一维弹道修正弹最小可修正射程很大程度取决于卫星定位接收机首次定位时间[8]。陈浩等研究了舵偏角与启控时间对修正能力的影响，得到启控时间越早，修正能力越强的结论[9]。但文章仅研究了弹丸在弹道降弧段的修正能力，未对升弧段与影响原因进行深入分析。

总体来说，针对旋转弹二维修正能力影响因素的研究还不够全面和深入，文中对在不同的翼面外形、发射点海拔高度、弹丸出炮口速度与炮口射角几个方面的影响进行了仿真分析。

1 舵修正力分析

1.1 不单独考虑舵片受力

弹丸气动参数通过气动力计算软件获得，且所得气动参数均在弹体系中表示。由于弹丸气动外形不对称，所求解的气动力和气动力矩只能表示在弹体系中。可依据是否与弹丸滚转角速度相关，将力和力矩分成两类：第一类与滚转状态相关，包括马格努斯力、马格努斯力矩、导转力矩和滚转阻尼力矩；第二类与滚转状态不相关。

修正组件和弹体所受的第一类力和力矩的幅值与方向和各自的滚转状态相关，故两者所受的同一种力不能作为合力综合作用在弹丸上，如修正组件和弹体所受的马格努斯力。因而，对于第一种力，只能在分别计算两刚体上所受的力和力矩后计算合力。

第二类力和力矩与弹丸质心速度和轴线的角速度相关，因修正组件和弹体的轴线重合，故可认为该类力是可综合作用在弹丸上，则有

(1)

式(1)中的力和力矩计算方法如下：

轴向力：Fx1=qsca，ca为轴向力系数，q为动压，s为参考面积；

法向力：Fy1=qscy,cy为法向力系数；

侧向力：Fz1=qscz,cz为侧向力系数；

法向力矩：My1=qslmy,l为弹丸特征长度，my为法向力矩系数；

侧向力矩：Mz1=qslmz,mz为侧向力矩系数；

1.2 单独考虑舵片受力

若单独考虑舵片升力，则将弹丸视为舵片、无舵修正组件和弹体三部分。无舵修正组件和弹体为旋成体，其气动力和气动力矩的描述相对较为简便。

定义操纵舵舵偏角为δz，弹体系下，舵片产生的气动力和气动力矩分别为：

(2)

式中：C′nδ为舵片的升力系数导数，lc为舵片压心到弹丸质心的距离。

无舵弹丸的与滚转状态无关的气动力和气动力矩直接在准弹体系表示如下：

(3)

与滚转状态相关的力和力矩的计算与上面相同。

2 影响因素仿真分析

弹丸在特定时间点起控后，将其修正舵稳定在某一特定角度，得到弹丸的仿真落点。固定弹丸的起控点，将修正舵稳定在不同的控制角度，得到一组弹丸的仿真落点；将仿真落点连接起来可得一条闭合曲线，该曲线即为该起控点起控后弹丸在控制下的落点极限边界。无控状态下的弹丸落点与极限边界的差即为弹丸的修正能力。文中将修正能力分为绝对修正能力与相对修正能力两部分，绝对修正能力是指弹丸进行修正后的实际修正距离，相对修正能力是指射程或侧偏上的实际修正距离与射程或侧偏的比值。

2.1 舵结构参数对弹丸修正能力的影响

图1～图4为安装不同结构参数舵的弹丸在不同时间点起控时的修正能力。通过图中数据，可将不同结构参数的舵的弹丸的修正能力进行统计，如表1所示。

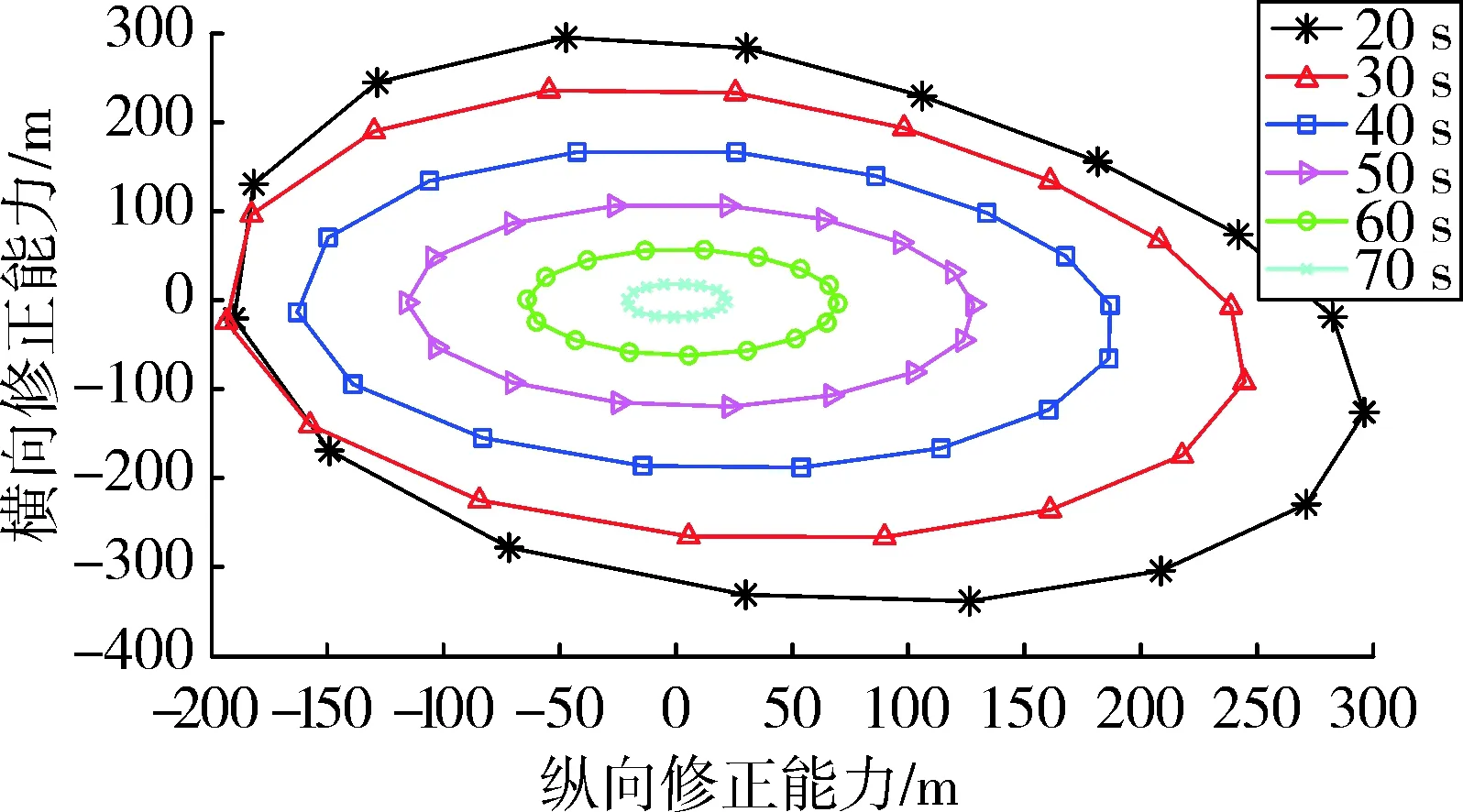
图1 不同起控时间时4°小舵片弹丸的修正能力

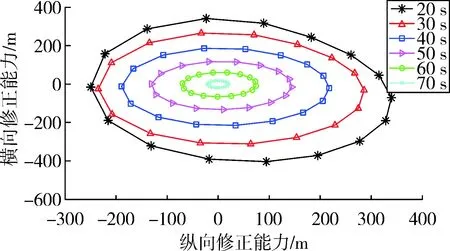
图2 不同起控时间时4°大舵片弹丸的修正能力

图3 不同起控时间时6°小舵片弹丸的修正能力

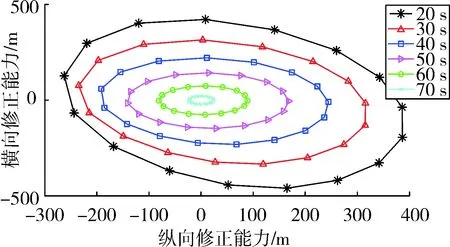
图4 不同起控时间时6°大舵片弹丸的修正能力

m

从表1中数据可知，无论哪种舵结构参数其修正能力均存在这样的现象：纵向远修修正能力小于纵向近修的修正能力，横向左修修正能力小于横向右修修正能力。该现象可解释如下：

弹丸在上升段起控并向远处修正，在修正控制作用下，弹道会高于无控状态下的弹道。存在某一时间点，将此时间点作为起控点可得最大的纵向远修修正能力。若起控时间晚于该时间点，有控弹道将低于该弹道，造成落点偏近；若起控时间早于该时间点，有控弹道的弹道顶点将前移，导致弹道提早进入下降段，造成弹丸落点偏近。图5为起控点分别为20 s和30 s的有控弹道的对比。图中，20 s起控的弹道在弹道顶点附近高于30 s起控的弹道，但随着弹丸的飞行，出现了20 s起控的弹道低于30 s起控的弹道的现象，造成了20 s起控的弹道落点偏近。

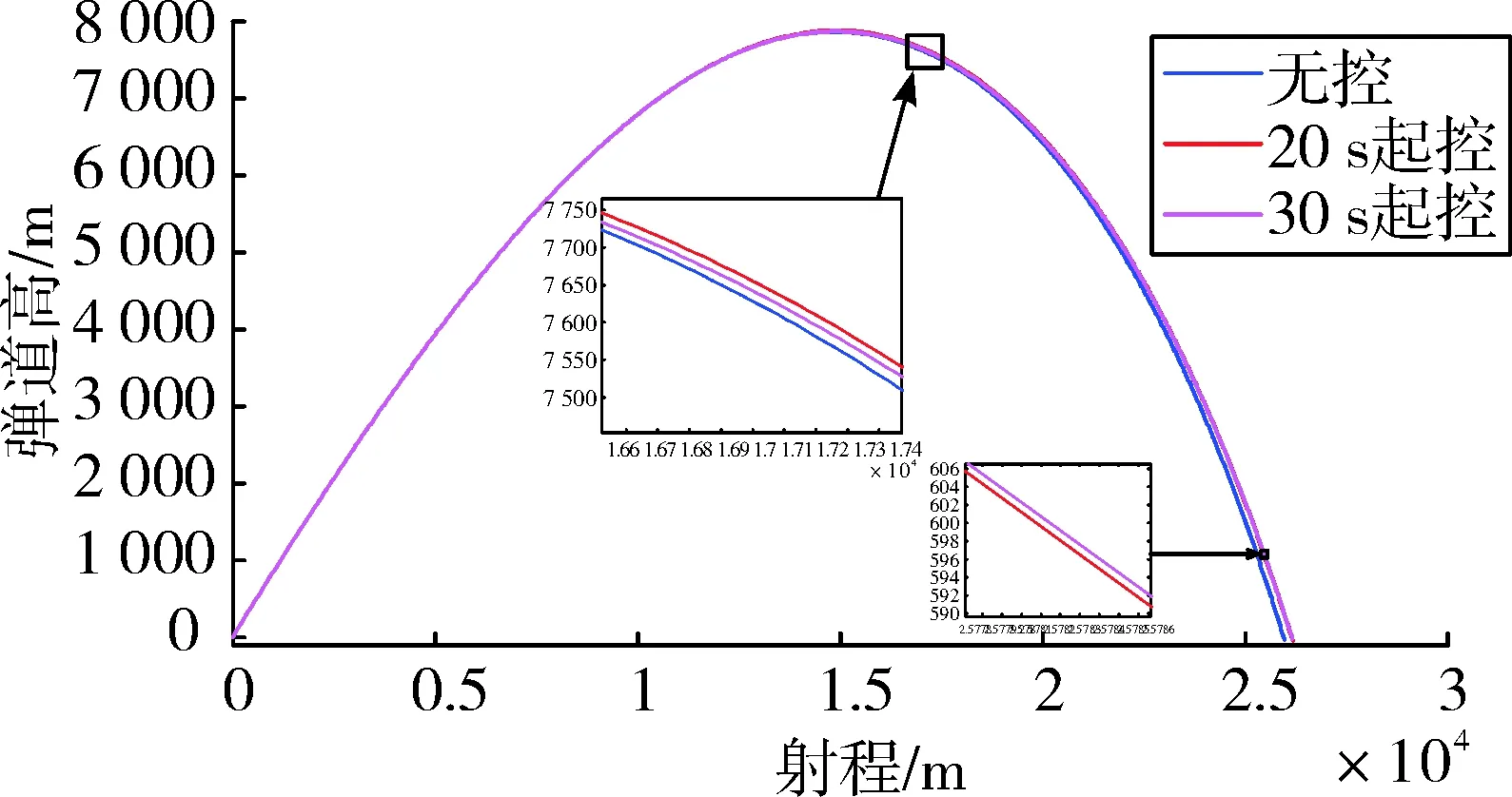
图5 不同起控点的弹道的对比

安装二维弹道修正引信的火箭弹、迫击炮弹、榴弹等弹箭在上升段进行纵向的向远处修正时，若起控点过早均会出现弹道变高、落点偏近的现象，造成弹丸修正不能达到预期目的。因而，在上升段均采用优先横向修正的策略。

右旋榴弹在飞行过程中，产生方向向右的动力平衡角以使弹轴追随弹丸的合速度方向。当弹丸左修时，通过调整舵相对于地面的滚转角使弹丸向右的动力平衡角减小；右修时，弹丸向右的动力平衡角增大。由于升力系数非线性的存在，增大的动力平衡角将使所产生的升力值大于减小的等值的动力平衡角的产生升力值，使弹丸的质心速度变化的绝对值不等，导致了横向右修的修正能力更大。

2.2 弹丸初速对修正能力的影响

在射角为40°，海拔为0 m，标准气象条件下，对不同发射初速弹丸进行分析。下文仅列出初速在800 m/s与900 m/s时不同时间点起控时的修正能力，如图6、图7所示。

图6 不同起控时间时800 m/s初速的弹丸修正能力

图7 不同起控时间时900 m/s初速的修正能力

通过仿真，将不同发射初速的弹丸的纵向远修、纵向近修、横向左修、横向右修所占射程与侧偏的百分比的相对修正能力进行统计，如表2所示。再将初速与相对修正能力绘制曲线，如图8所示。

表2 不同发射初速的弹丸20 s起控时的相对修正能力

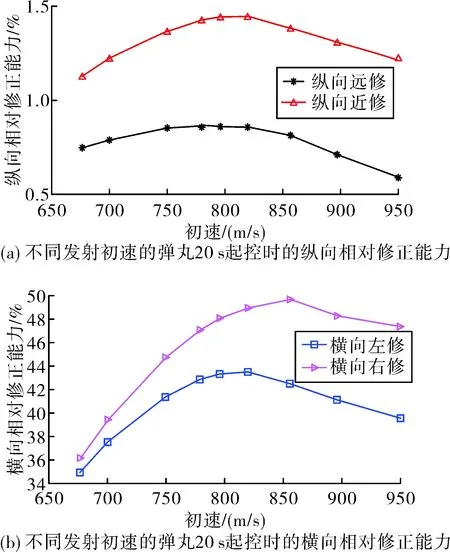
图8 不同发射初速的弹丸20 s起控时的相对修正能力

通过本小节图表的数据可知，弹丸的绝对修正能力随着初速的增大而逐渐增加，但在800～850 m/s之间时，弹丸的相对修正能力在纵向与横向近乎达到最大值。由图8可知，当初速在800 m/s时候，20 s进行修正的时候也出现提前进入下降段的状态，其解释与2.1相同。当初速继续增加的时候，该现象越明显，故在仅考虑该弹丸在20 s起控时的修正能力时，可得出初速在820 m/s附近时该弹丸的相对修正能力最大。

2.3 发射点海拔高度对弹丸修正能力的影响

在射角为40°，发射初速为900 m/s，标准气象条件下，对在不同海拔高度时发射的弹丸进行分析。仅列出海拔在2 000 m与3 000 m时不同时间点起控时的修正能力，如图9、图10所示。

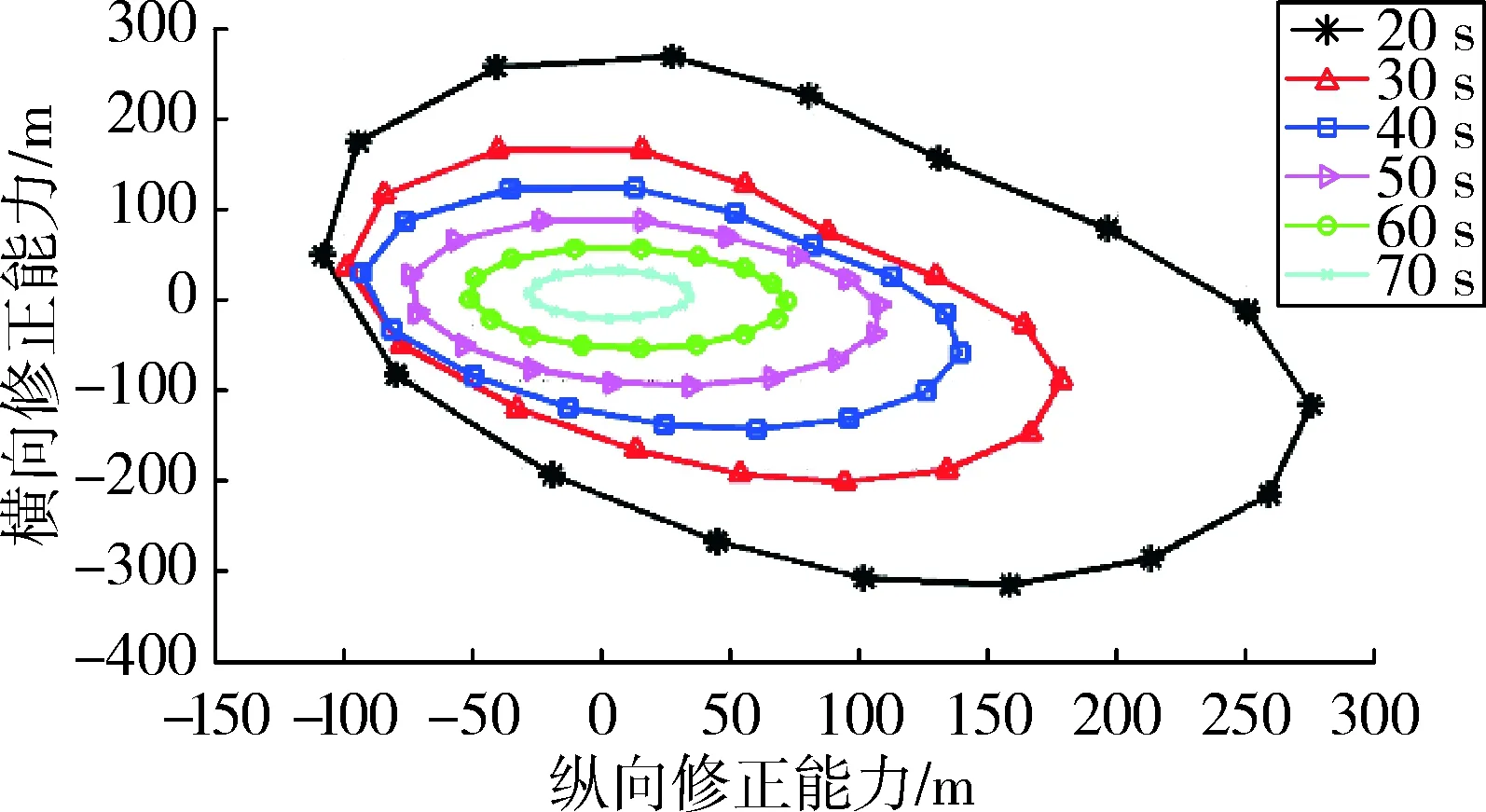
图9 不同起控时间时2 000 m海拔的弹丸修正能力

图10 不同起控时间时3 000 m海拔的弹丸修正能力

通过仿真，将海拔不同发射点的弹丸的纵向远修、纵向近修、横向左修、横向右修所占射程与侧偏的百分比的相对修正能力进行统计，如表3所示。再将海拔高度与相对修正能力绘制曲线，如图11所示。

表3 不同海拔的弹丸20 s起控时的修正能力

图11 不同海拔的弹丸20 s起控时的修正能力

通过图9～图11、表3，可以明显看到各项修正能力随着海拔高度的增加呈现出一个下降的趋势。根据压高公式：

空气的压强与密度在对流层中随着高度的增加而减小，使得弹丸在外弹道飞行的过程中其各项阻力系数减小，而射程与侧偏会相应增大，使得其修正能力下降。

2.4 炮口发射角对修正能力的影响

在海拔为0 m，发射初速为900 m/s，标准气象条件下，对在不同射角发射的弹丸进行分析。仅列出射角为30°与46°时不同时间点起控时的修正能力，如图12、图13所示。

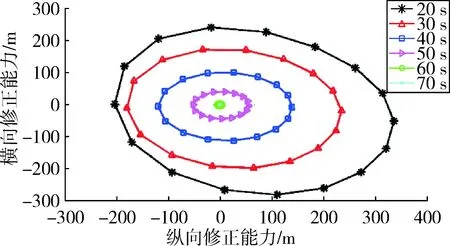
图12 不同起控时间时30°射角的弹丸修正能力

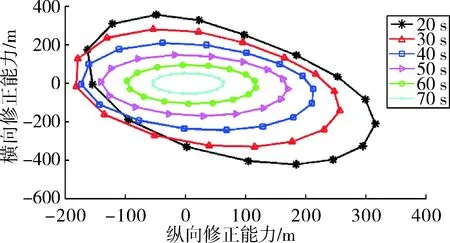
图13 不同起控时间时46°射角的弹丸修正能力

通过仿真，将不同出炮口射角的弹丸的纵向远修、纵向近修、横向左修、横向右修所占射程与侧偏的百分比的相对修正能力进行统计，如表4所示。再将海拔高度与相对修正能力绘制曲线，如图14所示。

表4 不同射角的弹丸20 s起控时的修正能力

通过分析图12～图14、表4，可以得出弹丸在近似以30°的射角发射时有最大的相对修正能力。观察图14可知，在30 s起控修正能力强于20 s起控的情况仅影响着纵向远修，而整体的相对修正能力呈现出在30°射角附近先增大后减小的趋势。相对于其它几种影响因素而言，射角的变化在纵向绝对修正能力上的变化并不大，而在横向绝对修正能力上的改变较大。由于修正能力是由舵的升力导致，所以在同一射角、不同控制角进行修正时，其射程与侧偏上的修正能力成正相关，在30°射角附近时，弹丸射程上的绝对修正能力达到最大，而无控弹丸侧偏的改变量明显大于射程的改变量，因而也使得弹丸的横向相对修正能力减小。

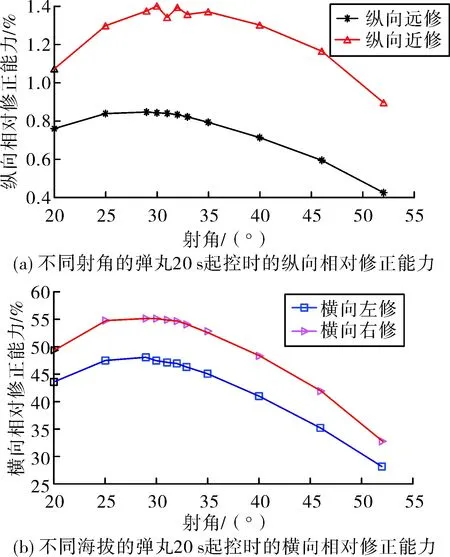
图14 不同射角的弹丸20 s起控时的修正能力

3 结论

文中以某型二维弹道修正旋转弹为例，对是否考虑舵片受力的弹丸所受力与力矩进行了建模分析，重点分析和研究了舵结构参数、发射点海拔高度、弹丸出炮口初速、火炮发射角度四个因素对弹丸修正能力的影响。结果表明弹丸纵向远修修正能力小于纵向近修的修正能力，横向左修修正能力小于横向右修修正能力；在研究初速对修正能力的影响时发现，弹丸的绝对修正能力随着初速的增大而增大，但其相对修正能力在820 m/s附近效果最好；在研究海拔对修正能力的影响时发现，随着海拔的增高，弹丸在射程与偏航上的绝对修正能力与相对修正能力都减小；在研究射角对修正能力的影响时发现，修正弹在30°射角附近有最佳的相对修正能力，其纵向射程上的绝对修正能力随射角的改变而变化的不大，横向偏航上的绝对修正能力随着射角的改变而变化较为明显。