基于DEPSORVM的B787电池剩余寿命预测

刘贵行 穆东旭

摘  要： 锂离子电池已经被应用于B787客机，为进一步提高B787锂离子电池的可靠性，针对传统基于相关向量机的电池剩余使用寿命预测方法的不足，提出一种把相关向量机、差分进化算法和粒子群优化算法融合的的方法。通过差分进化算法和粒子群优化算法对相关向量机的参数进行优化，增强其对电池历史监测数据退化趋势的预测能力。应用卡尔曼滤波器对融合算法实施优化，将优化后的预测结果作为在线样本添加到训练集中，对提出的模型重新训练，以此来动态调整系数矩阵和相关向量以执行下一次迭代预测。基于B787锂离子电池测量数据，对所提方法的有效性和鲁棒性进行了验证。

关键词： 剩余寿命预测; 相关向量机; B787锂离子电池; 差分进化算法; 粒子群优化算法; 卡尔曼滤波

中图分类号： TN36?34                               文献标识码： A                      文章编号： 1004?373X（2019）20?0094?05

Remaining useful life prediction for B787 plane battery based on DEPSO?RVM

LIU Guihang1， MU Dongxu2

（1. Engineering Technology Training Center， Civil Aviation University of China， Tianjin 300300， China;

2. School of Electronic Information and Automation， Civil Aviation University of China， Tianjin 300300， China）

Abstract： In allusion to the shortcomings of the traditional battery residual useful life prediction method based on correlation vector machine， a new method integrating RVM （relevance vector machine）， DE （differential evolution） algorithm and PSO （particle swam optimization） algorithm is proposed. The parameters of the RVM are optimized by the mean of DE algorithm and PSO algorithm to enhance its ability to predict the degradation trend of battery historical monitoring data. The Kalman filter is applied to optimize the fusion algorithm. The optimized prediction results is added to the training set as an online sample， and the proposed model is retrained to dynamically adjust the coefficient matrix and the correlation vector to execute the next iteration prediction. On the basis of the measured data of lithium?ion batteryused in B787 plane， the effectiveness and robustness of the proposed method are verified.

Keywords： RUL prediction; RVM; lithium?ion battery; DE; PSO; Kalman filter

0 引  言

在飛机电源系统中，航空蓄电池是一种核心备用电源，是飞机不可或缺的电力装置。航空蓄电池主要用于辅助航空发动机和辅助动力装置（Auxiliary Power Unit，APU）的起动、切换大功率负载时稳定飞机电源网络电压和作为应急电源向重要的应急设备供电[1]。

B787 锂离子电源均由锂离子电池组、电极、绝缘材料、排气孔和监视装置等构成，航空锂离子电源是典型的动态、非线性电化学系统，因此，航空锂离子电源的安全性和可靠性一直都是航空运输业十分关注的问题，一旦航空锂离子电源发生故障将导致极其严重的后果[2]。

锂离子电源故障预测问题已引起了国内外专家及研究机构的关注，大体上可分为基于模型的故障预测方法和基于数据驱动的故障预测方法[3]。基于模型的故障预测方法从锂离子电池电化学机理的角度出发，分析了电池在运作过程中的性能变化情况，构建了锂离子电池性能退化经验模型。基于模型的故障预测方法能够提供电池退化过程的物理分析和化学分析，但表征锂离子电池老化过程的模型复杂程度较高，且参数众多，因此在实际应用中，基于模型的故障预测方法难度较大，动态准确度较差。而基于数据驱动的故障预测方法不需要精确地构建描述电池内部运作机制的解析模型，因此避免了基于模型方法的缺点。通常情况下，人工神经网络（Artificial Neural Network，ANN）支持向量机（Support Vector Machine，SVM），相关向量机（Relevance vector Machine，RVM）算法是常见的数据驱动的方法。其中RVM是基于贝叶斯理论框架下的机器学习方法，与SVM算法相比，RVM方法有效地减少了计算负担，降低了时间的消耗，已被成功地用于锂离子电池的剩余寿命预测（Remaining Useful Life，RUL）[4]。文献[5]提出基于RVM的锂离子电池故障预测框架，实现了锂离子电池充放电时间的估计和预测。文献[6]提出一种基于RVM的锂离子电池可靠性计算模型，利用充电电压和电流作为提取的特征数据，能够准确估计电池容量，确保锂离子电池的可靠运行。基于数据驱动的方法仅需要状态监测数据的支持，是一种更为实用的预测方法。

B787客机锂离子电池（State of Health，SOH）监测数据在测量的过程中，由于受到随机负载、温度因素、电磁干扰和电池本身内部不可预知因素的影响，会包含各种类型的噪声。RVM算法中含有待调整参数，MacKay迭代估计法、EM（Expectation Maximization）迭代算法是常用的参数优化方法，但是此类方法是预测精度与计算负担之间的折衷[7]。为此，考虑到实际工业生产过程中的可实现性和可靠性，本文围绕航空锂离子电源故障预测这一主题，提出了基于差分进化算法（Differential Evolution，DE）、粒子群优化算法（Particle Swam Optimization，PSO）和RVM算法融合的DEPSO?RVM框架，为航空公司实现视情维修（Condition?based Maintenance，CBM）提供技术保障。

该方法把DE和PSO算法进行融合，利用融合后的DEPSO方法优化RVM算法中的参数;然后，应用卡尔曼滤波对DEPSO?RVM模型的预测结果进行降噪，以此削弱噪声等不确定因素对预测精度的影响，预测结果的不确定性表达以概率密度分布的方式给出;最后，基于B787锂离子电池的实测数据，验证了本文方法的有效性和鲁棒性。

1 RVM，DE和PSO的融合方法

1.1 相关向量机

RVM算法基于贝叶斯框架实施训练，在先验参数下删除无关向量点，其结构形式为权重和核函数的乘积。

1.2 差分进化算法

DE是Storn和Price提出的一种全局连续优化算法，给出一个D维空间向量[Xki=xki，1，xki，2，…，xki，D]，并且初始种群尽可能地覆盖整个空间。种群中的每个个体借助于式（5）进行变异操作。

差分进化算法具有较强的鲁棒性和适用性，可以很好地与其他算法融合，进而演化成性能更优的算法。

1.3 粒子群优化算法

PSO是由Eberhart和Kennedy开发的一种新的用于随机优化的进化计算技术。

算法被初始化为具有速度和位置的一组随机粒子（随机解），随后通过迭代计算更新粒子，找到每个粒子的局部最优解Pbest和全局最优解Gbest。假设粒子i的速度为[Vk+1i]，位置为[Xk+1i]，那么用于粒子速度和位置更新的公式可以表示为：

式中：[w]是惯性权重，用来调整搜索空间的大小;Pbest和Gbest分别表示单个粒子的局部最优解和全局最优解;[c1，c2]为加速系数，用于衡量粒子的历史最优解对其演化过程的影响程度;[r1，r2]是[0，1]内的随机数。当得到预先设定的结果后算法结束。

1.4  DEPSO?RVM模型的建立

针对DE和PSO算法分别在求解全局最优解的过程中由于过早收敛现象的发生导致陷入局部最优解的问题，提出了把DE和PSO融合的DEPSO方法。首先使用DE算法生成测试向量，如果测试向量的适应度高于目标向量，那么将其包括在种群中;否则激活PSO算法，使用局部搜索和全局搜索来生成另一个候选解。RVM具有处理小样本数据的能力，而训练算法是RVM的核心部分。通过似然函数和先验知识实现算法训练，其中似然函数描述训练样本的潜在特征，先验知识描述模型的复杂性，以此来增强对测试样本的泛化能力。

RVM超参数的选择直接影响电池容量的预测结果，例如权重参数[w]和核参数[σ]的取值决定了模型的稀疏性和泛化能力，为了准确预测B787客机锂离子电池的RUL，提出了DEPSO?RVM模型，并且提出了DEPSO方法来优化RVM中的超参数。文中的DEPSO?RVM模型的具体实施过程描述如下：

1） 设定[F，CR，Np，K]的值，并初始化式（5）中的向量[Xki]，设置[k=1]。

2） 在[0，1]之间随机选择[r1，r2]的值，并且根据式（5）建立突变载体向量[Vki]。

3） 执行式（6），通过交叉生成试验向量[uki]，如果生成的任一测试向量位于搜索空间之外，则在可行域内重新调整测试向量。

4） 将生成的测试向量与目标向量进行比较，如果测试向量的适应度值大于目标向量，则返回步骤2）并继续下一次迭代更新;否则，激活PSO算法。

5） 执行PSO算法，根据式（8）和式（9）更新向量[Xki，Vki，w]。

6） 如果[i≤Np]，返回步骤2）;否则执行步骤9）。

7） 把获得的新参数用作RVM模型的候选解，并且根据新的适应度更新Gbest的值。

8） 如果[k≤K]，返回步骤1）;否则执行步骤9）。

9） 把更新后的Gbest值用作RVM的被优化后的参数。至此，DEPSO?RVM建模完成。

文中的DEPSO优化算法与传统的MacKay迭代估计法、EM迭代算法相比能够提高计算效率，是一种能够均衡计算效率和计算稳定性的算法。

2 基于DEPSO?RVM的B787锂离子电池RUL预测

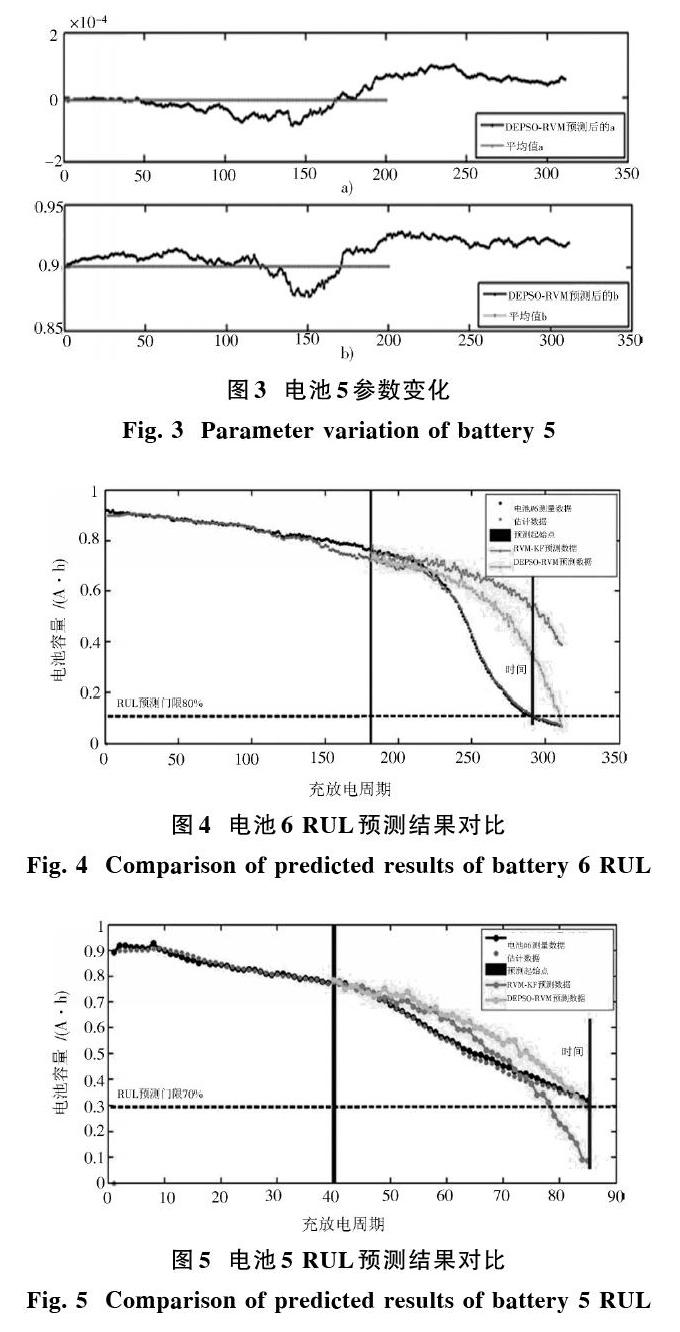
在本节中，从数据驱动的角度，根据所建立的DEPSO?RVM模型来预测电池容量和RUL。在实际工程应用中，由于测量噪声和其他潜在的不确定性因素的存在，会导致电池容量预测精度的降低。在这种情况下，使用KF算法来降低不确定性并获得更准确的结果，更具有普遍性。 此外，设备状态轨迹通常情况下是已知的，使用所提出的DEPSO?RVM方法不需要事先建立状态转换方程，可以对这个轨迹直接进行回归（核函数的加权和）。在每个时间步长内，设备状态的回归值遵循高斯分布：

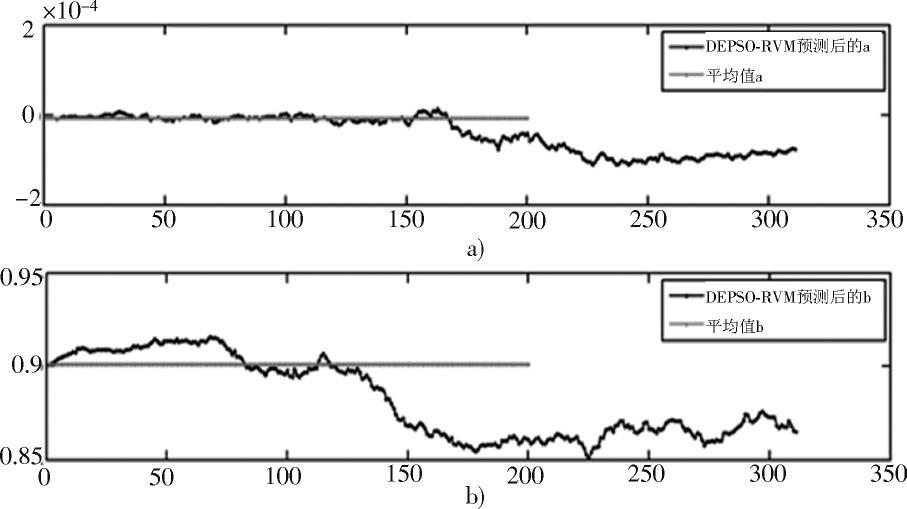
式中：[Ck]表示[k]时刻的放电容量;[ηC，k]定义为放电容量与同循环过程中充电容量的比值;[Δtk]表示时间间隔;[β1，k]和[β2，k]是容量再生项中需要确定的参数。根据传感器采到的监测数据，按照上述方法，通过建立的DEPSO?RVM模型直接回归训练数据，从而获取锂离子电池的退化趋势，并用其代替经验退化模型，此方法更适用于电池状态预测的动态应用。在此之后，使用KF对预测结果进行优化，降低噪声等不确定性因素带来的影响。至此就完成了PSO，DE，RVM等方法的融合过程，下面将给出具体的融合步骤。

4 结  语

本文提出一种预测B787客机锂离子电池RUL的迭代更新DEPSO?RVM算法。文章的主要贡献在于：

1） 针对单一的RVM算法在长周期预测过程中性能差的问题，提出一种用于B787客机锂离子电池RUL预测的迭代更新框架;

2） 把DE和PSO算法进行深度融合，利用融合后的DEPSO方法调整RVM算法中的未知参数;

3） 通过KF方法对最终的输出结果进行优化，削弱噪声污染，使RUL预测结果更为准确。实验结果表明，与传统的RVM方法相比，所提出的DEPSO?RVM方法拥有更高的预测精度和更好的可实施性。此外，所提出的DEPSO?RVM模型亦可以应用于其他领域的预测工作中。

参考文献

[1] 任仁良，万强，毕翔.航空锂电池的控制与保护[J].电源技术，2015，39（5）：902?904.

REN R L， WAN Q， BI X. Control and protection for aviation Li?ion battery [J]. Power technology， 2015， 39（5）： 902?904.

[2] 赵炜，孙晓，豆金昌.锂离子电池健康评估及剩余使用寿命预测方法研究[D].南京：南京航空航天大学，2013.

ZHAO Wei， SUN Xiao， DOU Jinchang. Health assessment and remaining useful life prediction of Li?ion battery [D]. Nanjing： Nanjing University of Aeronautics and Astronautics， 2013.

[3] 刘大同，周建宝，郭力萌，等.锂离子电池健康评估和寿命预测综述[J].仪器仪表学报，2015，36（1）：1?16.

LIU Datong， ZHOU Jianbao， GUO Limeng， et al. Survey on lithium?ion battery health assessment and circle life estimation [J]. Journal of scientific instrument， 2015， 36（1）： 1?16.

[4] PRASAD G K， RAHN C D. Model based identification of aging parameters in lithium ion batteries [J]. Journal of power sources， 2013， 232： 79?85.

[5] SONG Y， LIU D， HOU Y， et al. Satellite lithium?ion battery remaining useful life estimation with an iterative updated RVM fused with the KF algorithm [J]. Chinese journal of aeronautics， 2018， 31（1）： 31?40.

[6] ZHANG C， HE Y， YUAN L， et al. A novel approach for analog circuit fault prognostics based on improved RVM [J]. Journal of electronic testing， 2014， 30（3）： 343?356.

[7] YU H， WU Z， CHEN D， et al. Probabilistic prediction of bus headway using relevance vector machine regression [J]. IEEE transactions on intelligent transportation systems， 2017， 18（7）： 1772?1781.

[8] TIPPING M E. Sparse Bayesian learning and the relevance vector machine [J]. Journal of machine learning research， 2001， 1（3）： 211?244.

[9] LUO W， L? C， WANG L， et al. An approximate solution for electrolyte concentration distribution in physics?based lithium?ion cell models [J]. Microelectronics reliability， 2013， 53（6）： 797?804.

[10] POLA D A， NAVARRETE H F， ORCHARD M E， et al. Particle?filtering?based discharge time prognosis for lithium?ion batteries with a statistical characterization of use profiles [J]. IEEE transactions on reliability， 2015， 64（2）： 1?11.

[11] HU C， JAIN G， SCHMIDT C， et al. Online estimation of lithium?ion battery capacity using sparse Bayesian learning [J]. Journal of power sources， 2015， 289： 105?113.

[12] YIN S， DING S， ZHOU D H. Diagnosis and prognosis for Complicated industrial systems?part I [J]. IEEE transactions on industrial electronics， 2016， 63（4）： 2501?2505.

[13] LIU Y， WANG F， CHANG Y， et al. Multiple hypotheses testing?based operating optimality assessment and nonoptimal cause identification for multiphase uneven?length batch processes [J]. Industrial & engineering chemistry research， 2016， 55（21）： 6133?6144.