注重培养数学建模能力 提升数学核心素养
2019-11-12李永声
李永声

[摘 要]数学建模是应用数学解决实际问题的基本手段,培养学生的数学建模能力,对于发展其数学应用能力,提升数学核心素养具有十分重要的意义.
[关键词]思维能力;数学建模能力;核心素养;变量关系
[中图分类号] G633.6 [文献标识码] A [文章编号] 1674-6058(2019)26-0030-02
数学建模指的是对现实问题进行抽象,用数学语言表达问题,用数学知识与方法构建模型解决问题.在核心素养的导向下如何发展学生的数学建模能力是广大教师应当深入探讨与实践的重要课题.下面笔者根据自身的教学实践经验,围绕四个维度展开简单的论述.
一、分析变量关系,厘清数据
模型的假设和变量关系之间的确定对于数学建模来说是最为关键、最为重要的一步.如果变量关系理解错误,那么后续数学建模的过程都会变得没有意义.因而笔者认为,教师应当注重加强对学生分析变量关系的训练,引导他们厘清数据,然后根据变量关系建立数学模型,提高他们的数学建模能力.
比如,我在教学《一元一次不等式》时,组织学生对不等式模型进行探究与学习,引导他们通过训练感受数量间的不等关系.在课堂上,我向学生提出问题:某体育用品商城采购员要到厂家批发购买篮球和排球,共100个,要求付款额不得超过11815元,已知篮球的批发价为130元,商场零售价为160元,排球的批发价为100元,商场零售价为120元.(1)请问该采购员最多可以采购多少个篮球?(2)若该商城能够把100个球全部卖出,且所获得的利润不低于2580元,那么请问采购员要采购多少个篮球,可以盈利多少?随后学生开始分析题目中的数量关系,并构建不等式模型.例如,对于第(1)问,可以设篮球个数为x,那么130x+100(100-x)≤11815,解得x≤60.5.因为x要取正整数,所以最多可以采购60个篮球.
通过训练,学生能够对数据进行分析,将实际问题转化成相应的不等式问题,建立不等式模型,然后利用不等式的性质加以解决.
二、绘制图像表格,直观解读
数形结合是一种重要的数学思想,通过利用这一思想,学生可以“以形助数”、于“形”中觅“数”.根据图形去寻求几何关系,寻找解决问题的途径.我认为,教师要善于引导学生用图像、表格等去阐述数学问题中的数据关系,从而厘清思路、激活思维,对数量关系进行解读与剖析,提高数学建模的效率.
比如,教学《反比例函数》时,我引导学生学习几种常见的反比例函数的几何模型,然后提出问题:在直角坐标系中,一次函数y=k1x+b的图像与反比例函数y=k2/x的图像交于A(1,4)、B(4,1)两点,则△AOB的面积是 .为了解决这一问题,学生利用数形结合思想,绘制了如图1所示的图像,用待定系数法确定一次函数与反比例函数的解析式,再利用图像中的几何关系求解出△AOB的面积.紧接着,我对该问题进行变式.变式一:在直角坐标系中,一次函数y=k1x+b的图像与反比例函数y=k2/x的图像交于A(1,4)、B(3,m)两点,则△AOB的面积是.变式二:已知直线y=1/2x与双曲线y=k/x(k>0)交于A、B两点,且A的横坐标为4,求k的值.学生抽象出求解这类反比例函数问题的几何模型,如图2所示,若反比例函数y=k/x(k≠0,x>0)上任意两点P、C,过P作PA垂直与x轴于点A,过C作CD垂直x轴于点D,则证明△OPC的面积=梯形PADC的面积.
数学家华罗庚说过:“数缺形时少直观,形缺数时难入微.”我通过引导学生利用图形去探求数学问题中的数量关系,有效提高了他们的数学建模能力和数学核心素养.
三、寻找隐性规律,多元整合
很多数学问题,学生可以根据题目直接梳理出相应的数量关系,进而建立数学模型.然而有些时候,题目中的变量关系可能并不明确,这时候就需要学生去寻找题目中蕴含的隐性规律,并进行多元整合.因此,教师在对学生进行数学建模的训练过程中,应当增加问题的难度,使他们学会根据已经掌握的数据与线索来深度探究其中的隐性规律,然后进行整合建模.
比如,教学《一次函数》时,为了提高学生应用一次函数模型解决问题的能力,我提出问题:张老师从家里提着一个篮子打算去菜市场买10斤鸡蛋,已知篮子的重量为0.5斤,当菜市场的摊主将放好了10斤鸡蛋的篮子递给张老师时,他发现这次比以往买10斤鸡蛋的个数少很多,他再次让摊主称重,共称得10.55斤,但张老师却说这只有9斤的鸡蛋,要求摊主返还他1斤鸡蛋的钱.大家知道张老师是怎么知道摊主少称了大约1斤的鸡蛋呢?随后我开始引导学生探索题目中的隐含规律.设鸡蛋的实际重量为x,秤显示的重量设为y.若摊主没有作弊,则y=x;若摊主作弊,无非是想让y的值大于x.假设摊主为了让y>x,在秤盘底下加了吸铁石,此时的数量关系应为y=x+a.例如a为5两,那么称出来5斤的东西实际上是4斤5两,但是摊主事先并不知道顾客会买多少重量的东西.如果只买1斤的话,缺斤少两很容易被发现,因此可以推测摊主调整了他的秤,使得y与x的数量关系为y=kx(k>1).由此可以建立一次函数模型:k(x+0.5)=10.55.又因为10=kx,两式联立可以得到k=1.1,x=9.09,也就是说摊主少了张老师大约1斤的鸡蛋.
我通过设计题目,引导学生去探究其中的隐含规律,进一步帮助他们强化课堂所学知识,提高了他们思维的灵活度,取得了很好的教学效果.
四、结合现实生活,学以致用
数学来源于生活,又应用于生活.新课标明确提出了“教学生活化”的要求.由此可見,广大教师要注重结合现实生活设计题目,引导学生进行数学建模的训练,使他们在学习过程中,能够在实际的生活情境中发现和提出问题,针对问题建立数学模型并求解,提升他们的数学应用能力,使他们做到学以致用.
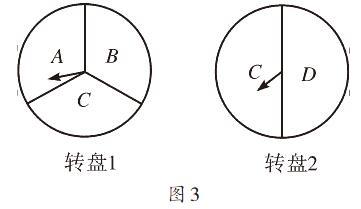
比如,教学《等可能条件下的概率》时,我引导学生体会并学习描述不确定现象的数学模型,学生知道了等可能条件下概率的计算方法:P(A)=m/n.其中m代表事件A发生可能出现的结果数,n表示一次试验所有可能出现的结果数.为了提高学生应用这一数学模型求解实际问题的能力,我联系现实生活,设计了如下练习题:为举办毕业联欢会,小利设计了一个游戏,游戏者分别转动如图3所示的两个可以自由转动的转盘一次,当两次转盘的指针所指的字母相同时,他就获得了一次指定一位到会者为大家表演节目的机会,那么这种机会获得的可能性到底有多大呢?请大家尝试利用所学概率知识计算参与一次游戏获得这种指定机会的概率.学生首先用列表的方法表示出了所有可能出现的结果,然后根据上述数学模型,求解得到了概率为1/6.
我结合实际生活,设计有关数学建模的练习题目,使学生认识到生活中的概率问题,体会到概率模型在生活中的应用与价值,拉近了数学与学生的距离,有效激发了他们学习数学的兴趣.
总而言之,培养学生的数学建模能力,有助于使他们在数学核心素养的形成过程中,积累用数学知识解决实际问题的经验,使之学习“有用的数学”,实现新课标的教育主张,提高课堂教学的效果与质量.广大教师在教学过程中应当重视和培养学生在数学建模方面的能力,善于设计多元的数学建模活动与探究活动,不断发展其数学核心素养.
(责任编辑 黄桂坚)