几何画板在数学教学中的应用探索
2019-11-12李如咬
李如咬


[摘 要]结合具体教学案例,分析几何画板在数学教学的应用,突显几何画板辅助数学教学的特有优势:体现数学源于实践,源于生活;体现“以学生发展为本”;体现“数学是数学活动的教学”;体现数学的实质内涵.
[关键词]几何画板;数学教学;应用
[中图分类号] G633.6 [文献标识码] A [文章编号] 1674-6058(2019)26-0009-03
在初中阶段,图形的特征认识及其相关的证明以及函数图像这些图形类的内容是学习的重点,也是学习的难点,更是困扰很多学生的“结”点.学生对图形缺少实际的认识,对规律的认识只停留在概念的层面,难以进行串联性记忆和综合运用.如何让数学课“活”过来,让学生最大限度地释放数学思维的火花,很值得我们思考.
几何画板让几何“活”了,数学“动”了.几何画板的最大特点就是“动态性”,并具有简明、朴素、短小的特点,拥有强大的图形、图像和动画功能,具有入门容易、操作简单、节省资源等优点.几何画板为学生提供了一个进行几何实验的环境,为教师和学生提供了一个探索几何图形内在关系的平台.因此,研究几何画板在数学教学中的应用有着重要的意义.
一、利用几何画板调动学生的学习积极性
在数学教学中,教师发现能真正领悟数学之美的学生很少.其原因大多是教师受传统教学模式的影響,课堂上讲的内容太多,留给学生独立思考、讨论练习的时间太少,学生觉得数学学习枯燥无味,容易出现倦怠、厌烦等不稳定情绪,慢慢地,也就失去了学习数学的兴趣.几何画板集图、声、色、文于一体,能让学生清楚地看到图形变化的全过程,化静为动、化繁为简、化虚为实,使枯燥的数学知识趣味化,提高学生主动探究的积极性,激活学生的创新思维.
二、利用几何画板设计生动的问题情境
一个好的问题情境的设计能激发学生的学习兴趣和探究欲望,能使教师教得轻松,学生学得愉快.而利用几何画板可设计生动的问题情境.
例如,九年级数学上册《图形的旋转》的教学中,教师首先给学生展示了几个美丽的动画,当动画结束时,出现了一个个美丽的图案(如图1).学生被这些美丽的图案迷住了,立即产生了浓厚的学习兴趣.这样的开始就预示着课堂教学已成功了一半.在好奇心的驱使下,学生就会结合具体情境,运用已有知识,借助类比、联想、猜测等方法,与教师共同探索,进行知识迁移,掌握“旋转”的概念、性质,学会如何进行旋转作图.随着对图形旋转概念的深入理解,学生会迫不及待地亲自动手设计图案,教师可适时给予帮助和指正,让学生感受到学习成功的喜悦.
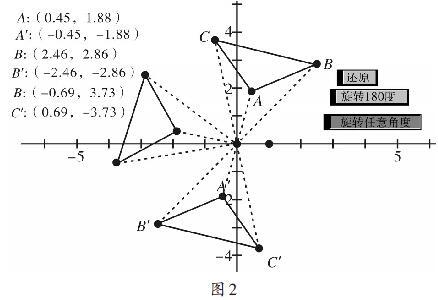
同一章节中的中心对称的知识,也可借助几何画板加深学生对其变换过程中坐标变化的认识.如图2中,任意拖动点A、点B、点C、点A′、点B′、点C′中的任一点,改变其线段的长度或方向,图中的坐标都会随后展现准确的数值,能让学生直观地观察到各对应点的横、纵坐标都变为原对应点的横、纵坐标的相反数.
三、利用几何画板指引探究型问题的思考方向
美国实用主义教育学家杜威认为,教学过程是学生直接经验的不断改造和增大意义的过程,即“从做中学”的过程.学生应该在做事中学习,做事的过程也就是从做中学的过程.
例如,讲授《直线与圆的位置关系》新课之前,我让学生收集了大量相关的实际素材,同时设计了一些适合学生探究的问题,并尝试使用几何画板制作如下课件以加强视觉感.其中,对直线与圆相切的理解是学生的思维难点,也是本节教学的重点.
课件的基本操作如下:
(1)如图3,画出一个半径为r的圆O以及任意一条直线[l],过点O作直线[l]的垂线,垂足是E.
(2)拖动直线[l]上任意一点A、点B或整条直线[l],改变直线与圆的位置关系,让学生从不同的动态效果多角度地观察与思考:直线[l]与圆有几个交点?同时跟踪线段OE的长度(即圆心O到直线[l]的距离)变化,比较它与半径r的大小关系.
实验操作后,学生可以总结变化过程中各种位置关系的特征:当直线[l]与圆有两个交点时,直线与圆相交,且OE
又如,《切线长定理》一节中,也可以设置活动的图形探寻过圆外一点切线长的形成和切线长定理的有关内容.
为了便于学生理解和操作,如图4,假设圆外一点P,在圆上取一点B,拖动B点在圆上搜寻并跟踪观察何时[∠PBO]等于[90°],结合此时[∠PBO]的角度和切线长定理易知:PB[⊥]OB,另外不难发现[∠PAO]等于[90°],PA[⊥]OA,即PA、PB都是圆O经过P点的切线.
学生还可以自主地发现线段PA、PB的长度关系,OP分[∠APB]为相等的两个角,即OP是[∠APB]的角平分线.在此猜测的基础上,结合相关的条件和定理不难证明这些结论的正确性.
创设探究型问题,让学生动手操作、实验、总结,这种带着问题的探索是一种模拟数学家探寻结论的类似情境.启发学生像前人那样,主动地观察,独立地研究,感受数学知识的形成和发展的奇妙过程.实践出真知,让学生在实践操作中学习数学,感受数学的美,增强学生学习数学的兴趣,让学生轻松掌握数学知识.
四、利用几何画板培养学生的创造力
几何画板除了帮助学生理解概念,使一些抽象、难懂的定理变得易于掌握外,还能弥补传统解题中的直观性、立体感和动态感等方面的缺陷.
例如,求证等腰三角形底边上任一点到两腰的距离之和等于一腰上的高.
如图5,等腰三角形ABC中,AB=AC,BC上任意一点D,DE⊥AB于E,DF⊥AC于F,BH⊥AC于H.求证: DE+DF=BH.该题是八年级比较典型的一道开放性证明题,难度不大,但很经典,证明方法很多.
在几何画板中,能生动地看到每种变化有可能带来的突变.
变化一:当D点在BC的延长线或反向延长线上时,结论就会发生变化,即[DE-DF=BH].
变化二:当D点运动到等腰三角形的内部设为点O时(如图6),视等腰三角形的形状而定.(1)当三角形是顶角小于[60°]的等腰三角形时,三段高的和大于腰上的高;(2)当三角形是顶角大于[60°]的等腰三角形时,三段高的和小于腰上的高;(3)当三角形是有一个角为[60°]的等腰三角形,即正三角形时,就有“正三角形内任意一点到三边的距离的和等于等边三角形的一条高”的结论.
变化三:当点运动到等边三角形的外面时,结论形式虽有所不同,但研究道理是相似的.
如图7,设点P是等边三角形外一点,P到三角形ABC三边AB、AC、BC(或其延长线)的距离分别为[h1,h2,h3],三角形ABC的高为h.通过数据跟踪观察结合计算结果,学生很容易接受和理解得出的結论:[h1+h2-h3=h].几何画板让比较难懂的知识变得易于理解,同时逐步培养了学生的抽象概括能力.在经历了自身的动手操作后,将无形的知识通过有形的操作来掌握,将无趣的数学学习变为有趣的数学学习,使学生对知识的形成感到亲切、自然,进而轻松愉快地掌握了知识.
五、利用几何画板架设数形结合的桥梁
著名数学家华罗庚说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休.”数形结合是一种非常重要的数学思想,在数学发展过程中,数与形结合在一起,内容上互相联系,方法上互相渗透,并在一定的条件下可以互相转化.运用数形结合思想,可以使数与形各展其长,使逻辑思维与形象思维完美地统一起来.而几何画板为我们提供了这样的平台.
静态的图形、图像使原本相互联系的知识割裂开来,失去了知识之间的内部联系,会使学生只注意事物的局部而忽视整体.几何画板能动态地展示问题的特点,可以克服静态图形的缺陷.
例如,九年级下册《相似》一章中,研究三角形内接矩形的面积变化规律的“数学实验”.如图8,在△ABO中,C是OA边上的任意一点,以C为顶点作△ABO的内接矩形CDEF,使矩形的一边CD在OA上,点C在OA上运动,矩形CDEF的面积随之变化.设OC为x,建立x与矩形面积S间的函数关系.让学生探究,当x变化时,矩形面积的变化特点及是否有最大值.
通过制图,设立关于x与面积S=FC [×] FE的参数函数,然后几何画板自动显示当C点运动时,对应的动点I(x,S)(S为矩形面积)的运动轨迹(其轨迹为开口向下的一段抛物线).不断改变△ABC的形状,研究△ABC的底边OA或OA边上的高变化时,对抛物线形状有什么影响.当已知OA与OA上高的值时,我们就可以算出x等于多少时,矩形CDEF的面积最大.
对于较复杂、抽象、需有一定想象能力的问题,教师光用嘴和笔常常说不清楚,借助于几何画板强大的图形、图像功能,把“数”与“形”紧紧结合在一起,将数学实验引入课堂教学中,可以活跃课堂气氛,减轻教学负担,大大激发了学生的学习兴趣和促进了学生认知主体作用的有效发挥.
以上便是我利用“几何画板”在数学教学中的一些尝试与探索,几何画板作为现代信息技术与教学整合的一项杰出创作,应用几何画板可以提高数学教学的直观性和准确性,弥补了传统教学方式在直观感、立体感和动态感等方面的不足,让学生更深刻地体会到数学“动”的一面,从而达到改进部分章节教学方法和手段的目的,更好地提高课堂教学的有效性.真正体现课堂教学中学生的主体地位和教师的主导地位,对提高学生的数学素质和教师的教学能力有着重要的作用,同时也对我国的素质教育起着重要的推进作用.
[ 参 考 文 献 ]
[1] 王伍增.新编多媒体课件制作培训教程:计算机职业培训丛书[M].北京:化学工业出版社,2008.
[2] 中华人民共和国教育部.普通高中数学课程标准(实验)[S].北京:人民教育出版社,2003.
[3] 缪亮.几何画板辅助数学教学[M].北京:清华大学出版社,2006.
(责任编辑 黄桂坚)