永磁同步电动机超螺旋非奇异快速终端滑模转速控制
2019-11-12吉洪智赵朝会胡怡婷建照阳
吉洪智, 赵朝会, 胡怡婷, 丁 帆, 建照阳
(上海电机学院 电气学院, 上海 201306)
永磁同步电动机(Permanent Magnet Synch-ronous Motor, PMSM)的直接转矩控制(Direct Torque Control, DTC)技术首先由德国的Depen-brock和日本的Takahashi提出。1997年,Zhong等[1]将这种技术应用于PMSM的控制。DTC结构简单、鲁棒性强,但是同时也存在转矩脉动大、开关频率不恒定等问题[2-3]。为了解决该问题,国内外学者提出了许多改进技术[4-8]。文献[4]详细介绍了应用空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM),DTC的转矩脉动大大减少,控制性能提高。文献[7]介绍了采用预期电压矢量计算单元来代替传统DTC中的磁链以及转矩滞环比较器,可以有效地减小转矩脉动并对其进行优化。文献[8]提出了一种结合DTC与空间矢量调制的方法,从而使得开关频率保持恒定并且降低了转矩脉动,但这种方法仍无法高精度地控制系统的稳态特性以及鲁棒性。
滑模变结构具有较高的稳态精度和较小的超调量,因此,这种方案具有很强的鲁棒性。结合智能控制理论,学者们提出模糊滑模控制器、非奇异终端滑模控制以及高阶滑模的控制思想等,都不同程度地改善了系统鲁棒性、低速性能以及削弱抖振,但不同方法也有局限性[9-11]。文献[12-14]介绍了滑模控制技术逐渐应用于电机控制及航空航天等领域。文献[15]研究了一种全局非奇异快速终端滑模结构,提高了系统的稳定运行能力。文献[16]分析了将两个PI控制器替换成超螺旋(Super-twisting)滑模变结构控制器,减少了抖振且超调量较小。文献[17]介绍了基于非奇异终端滑模的模型预测转矩控制的研究,改善了转矩脉动和转速的动态响应。
本文将Super-twisting非奇异快速终端滑模控制器用于控制系统的转速环,并对采用Super-twisting非奇异快速终端滑模控制器和采用传统PI控制器进行仿真对比,期望该滑模能够解决超调频繁的问题,提高转速响应速度,减小转矩脉动以及超调量。
1 基于SVPWM的PMSM DTC
DTC中,PMSM在d-q坐标系下的电磁转矩方程为
|ψs|(Lq-Ld)sin 2δ]
(1)
式中:Ld,Lq分别为d轴和q轴定子电感;p为极对数;Te为电磁转矩;ψs和ψf分别为定子磁链和转子永磁体磁链;δ为转矩角。
对式(1)求导,可得
(2)
由此可见,转矩的变化与转矩角的变化是非线性关系,即
2|ψs|(Lq-Ld)cos 2δ]Δδ
(3)
式中:ΔTe为转矩增量;Δδ为转矩角增量。
从式(3)可以看出,由于PMSM的转子磁链为定值,当控制定子磁链ψs为一固定值时,且不考虑ψs变化对转矩的影响,ΔTe就取决于Δδ。其坐标系如图1所示。

图1 转矩角增量坐标系
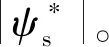
根据图1,可以将PMSM在α-β坐标系中的电压方程改为
(4)
式中:uαref,uβref分别为α,β轴期望电压分量值;ΔT为控制周期。
期望电压矢量的幅值和相位角可以通过式(4)得出
(5)
由式(5)可确定期望电压所在区间及大小,从而由电压空间矢量调制单元产生SVPWM脉冲信号,控制逆变器驱动永磁同步电动机运行。
2 控制原理
2.1 滑模面选取
定义系统的二阶非奇异快速终端滑模变量,可以有效避免滑模面的奇异现象,即
(6)
式中:e为系统状态误差;0<α<1;β∈R+;p,q∈N且为奇数;λ>p/q且1
当系统的状态远离平衡点时,转速误差e会较大,由上述滑模面可以看出,转速误差e的高次项起到了决定性作用,所以其收敛速度会比非奇异终端滑模的收敛速度更快。
2.2 Super-twisting控制律设计
电动机机械运动方程为
(7)
式中:J为转动惯量;Te为电磁转矩;TL为负载转矩;B为阻尼系数;ωm为电动机机械角速度。
式(7)可改写为
(8)

(9)
将式(8)代入式(9)得
(10)

(11)

(12)
(13)
式(13)可以改写为
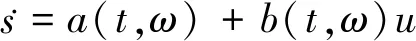
(14)
式中:ω为状态变量;u为控制输入量;a(t,ω)和b(t,ω)均为不确定函数,且满足
(15)
式中:A,Bmin,Bmax∈R+。
采用Super-twisting算法可使系统的相轨迹在一定时间内绕原点作螺旋式的旋转,算法如下:
(16)
Super-twisting算法在滑模面上收敛和稳定的充分必要条件为
(17)
控制器稳定性证明如下:
(18)
将式(12)和式(14)代入式(18)得
(19)
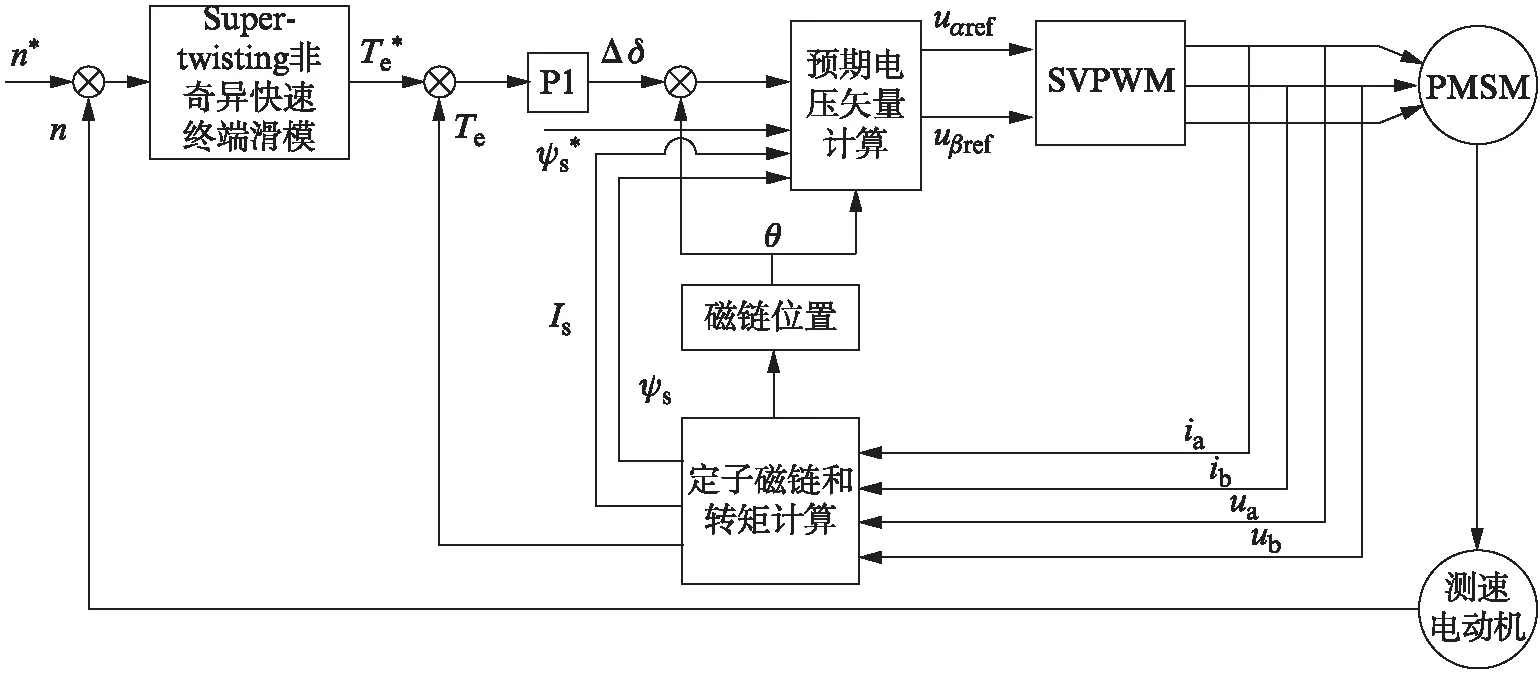
由式(15)可得|a|≤A,0 (20) (21) 因此,式(21)满足Lyapunov稳定性定理,说明系统稳定。 根据式(6)和式(16),可以得到图2所示的控制器框图。 系统整体控制框图如图3所示。 图2 基于Super-twisting非奇异快速终端滑模速度控制器框图 图3 基于Super-twisting非奇异快速终端滑模的PMSM直接转矩控制框图 本文采用Matlab/Simulink仿真软件,建立了基于Super-twisting非奇异快速终端滑模的永磁同步电动机直接转矩控制仿真模型。转速控制器分别采用传统PI控制器以及Super-twisting非奇异快速终端滑模控制器,其余电动机参数与仿真参数均不变,将两者进行对比分析。 电动机的参数如下:定子电阻为为0.958 5 Ω,定子电感为5.25 mH,转子磁链为0.182 7 Wb,转动惯量J为6.329×10-5kg·m2,极对数为4。额定转速设为1 000 r/min,定子磁链给定值为0.2 Wb,控制系统采样周期为1 μs。电动机的运行过程如下:在t=0 s时启动电动机,给定启动速度为1 000 r/min;在t=0.05 s时,负载转矩由0 N·m突变到5 N·m。所得的仿真结果如图4~6所示。 图5 转矩波形对比 图6 转矩放大波形对比 图4~图6中实线为采用传统PI控制器波形,虚线为采用Super-twisting非奇异快速终端滑模控制器波形。从图4中可以看出,采用传统PI控制器时,转速波形需要12 ms时才能达到额定值1 000 r/min,并且启动过程中存在超调频繁的问题;而采用了Super-twisting非奇异快速终端滑模控制器,可以在3 ms时达到额定转速,其动态响应速度快。从图5可以看出,在启动和突加负载时,采用Super-twisting非奇异快速终端滑模控制器时转矩波形都能够很快达到额定转矩,而使用PI控制器都存在一定的超调。图6中采用PI控制器的波动范围为4.75~5.25 N·m,转矩脉动为0.5 N·m;而采用Super-twisting非奇异快速终端滑模控制器的波动范围为4.91~5.06 N·m,转矩脉动为0.15 N·m,对比可以看出使用super-twisting非奇异快速终端滑模控制器时,转矩脉动更小。 本文研究了在永磁同步电动机空间矢量DTC中采用Super-twisting非奇异快速终端滑模控制器时的转速和转矩波形。系统的转速环用Super-twisting非奇异快速终端滑模控制器代替传统PI滑模控制器。仿真结果表明,在空间矢量DTC中采用Super-twisting非奇异快速终端滑模控制器有以下优点:① 转速的响应速度提高了9 ms;② 转矩脉动减小了0.35 N·m;③ 解决了频繁超调的问题。3 转速控制

4 仿真与分析


5 结 语
