一种新的轴承故障诊断方法

张荣涛， 焦 斌， 李彬彬

(上海电机学院 电气学院， 上海 201306)

在设备状态监测和故障诊断中旋转机械是最易出故障的部分，而在旋转机械的故障中滚动轴承的故障占据了较大一部分，据不完全统计，滚动轴承作为旋转机械中容易损坏的部件之一，其引起的故障在旋转机械的故障中约占30%[1]，因此，对于轴承运行状态的监测和故障诊断一直是科学工作者的一个重要的研究课题。一般而言，轴承主要由保持架、滚珠、内圈和外圈组成，最广泛的检测与诊断方式是通过振动传感器采集轴承的振动数据，针对振动数据进行特征提取[2]，提取的时域参数[3]往往能够轻易地分辨出故障类型，尤其是峭度[4]，在轴承正常运转状态时，峭度指标K≈3，由于在设备的复杂性和设备所处的环境多变性的多种因素的影响下，振动信号的概率密度分布接近于正态分布；随着故障的出现且慢慢变大，振动信号中幅值较大的振动点的概率密度值升高，正态曲线开始变形，此时的峭度值也随之变化，变形越严重，峭度值越大，相应的故障越严重，当K>8时，有很大可能出现了较严重的故障。但对于早期故障或者是保持架和滚珠的故障，由于其故障频率与转频相差不大并且振幅偏小，所以难以分辨出是否为正常轴承。

本文针对轴承时域参数中正常数据与故障数据区分困难的问题，将提取图像局部纹理特征的局部二值模式(Local Binary Pattern, LBP)算法引入到轴承的故障诊断中，首先应用改进的LBP算法将一段振动数据转变成LBP数据段，然后提取此数据段的样本熵作为特征元素，与人工提取的特征元素混合组成特征向量，最后通过XGBoost算法判断轴承的运行状态。XGBoost算法是对梯度增强决策树(Gradient Boosting Decision Tree, GBDT)算法的高效实现，GBDT的实现是比较慢的，而XGBoost的特点就是计算速度快，模型表现好。因此，本文提出了基于LBP样本熵XGBoost算法的轴承故障诊断方法。

1 LBP样本熵

1.1 样本熵

样本熵[5](SampEn)是基于近似熵(ApEn)的一种用于度量时间序列复杂性的改进方法，就是将一段非平稳时间序列分成有限个模态，将每一个模态与其他模态相对比，求出在一定阈值内与该模态相似的个数，然后通过计算求出新模态出现的概率，从而计算出该时间序列的复杂性，

设维数为m时，时间序列的自相似概率为B；维数为m+1时，时间序列的自相似概率为A，得出相邻维数时，时间序列的自相似概率比值CP=A/B。近似熵的计算是以-ln(CP)为模型，然后计算出所有模型的平均值。为了防止出现计算ln(0)的情况，近似熵在算法的第4步中受到了自身向量的影响，在计算上有偏差存在。但是与近似熵不同，样本熵是先求取自相似概率的和，然后取对数，这样不会受到自身向量的影响，所以其优势在于包含更大的A、B以及更加准确的CP估计。

样本熵与近似熵相比，有两大优越性：数据长度对样本熵的计算无影响；样本熵具有更好的一致性，即每个参数的变化对样本熵的影响程度是相同的。

1.2 LBP算法

LBP是在对图像的局部纹理特征提取时，描述纹理特征的一种算子，也称为局部二值模式[6]。其基本原理是在一个如图1所示的窗口内，将中心像素周围8个像素的灰度值分别与中心像素的灰度值进行比较，LBP算法计算原理如下：

(1)

图1 LBP变换

式中：(xc,yc)为中心像素的位置；ic为中心像素的灰度值；ip为中心像素的相邻像素的灰度值；s为一个符号函数。

若周围某点的像素值比中心的像素值大，则标记该像素点的位置为1，否则标记为0，代入式(1)可得中心向素的LBP值LBP(A)=000100112=1910.

1.3 LBP样本熵

因为LBP算法提取的是图像的局部纹理特征，所以将其应用于滚动轴承故障信号的检测，表征的是中心幅值在应属窗口中的重要性，针对轴承振动信号取1个1×k(k为奇数)窗口，同样将窗口中心元素作为阈值，将其他k-1个元素一一与其比较，一维LBP算法的计算公式如下：

(2)

式中：tc为中心元素的发生时间；xc为中心元素的振动幅值，xc-为左边相邻的振动幅值，xc+为右边相邻的振动幅值。

通过式(2)将一段振动数据转变成LBP数据段，然后提取此数据段的样本熵作为特征元素来判断轴承的运行状态。

2 XGBoost算法

2.1 算法原理

本文将在举办机器学习竞赛和代码分享的平台(kaggle)的很多比赛中将表现异常出众的XGBoost算法应用到滚动轴承的故障诊断中。XGBoost就是对GBDT的实现，一般来说，GBDT[7]的实现是比较慢的，而XGBoost[8-13]的特点就是计算速度快，模型表现好。XGBoost作为监督学习的非参数模型，其参数的选择取决于用于模型的训练数据，与GBDT最大的不同点在于损失函数，GBDT在计算目标函数时只用到了损失函数的一阶导数，而XGBoost对损失函数用二阶Taylor展开近似为

(3)

式中：f(x)为实际的输出结果；f(x+Δx)为预测的输出结果。

XGBoost中关于弱学习器树的定义也有所不同：把树拆分成结构部分q和叶子分数部分w。新定义的树的模型为

φ(x)=wq(x)，w∈RT，q∶Rd→{1,2,…,T}

(4)

式中：q为结构函数，能够把输入映射到叶子的索引号；w为每个索引号对应的叶子的分数；T为树中叶子结点的数目；D为特征维数；R为树的结构集合。

树的复杂度定义为

(5)

式中：γ为L1正则系数；λ为L2正则系数。由式(5)可知，γ与λ共同决定着弱学习器树的复杂程度。

2.2 参数调整

本文调用Python中的XGBoost模块对数据进行分析，主要参数如表1所示。

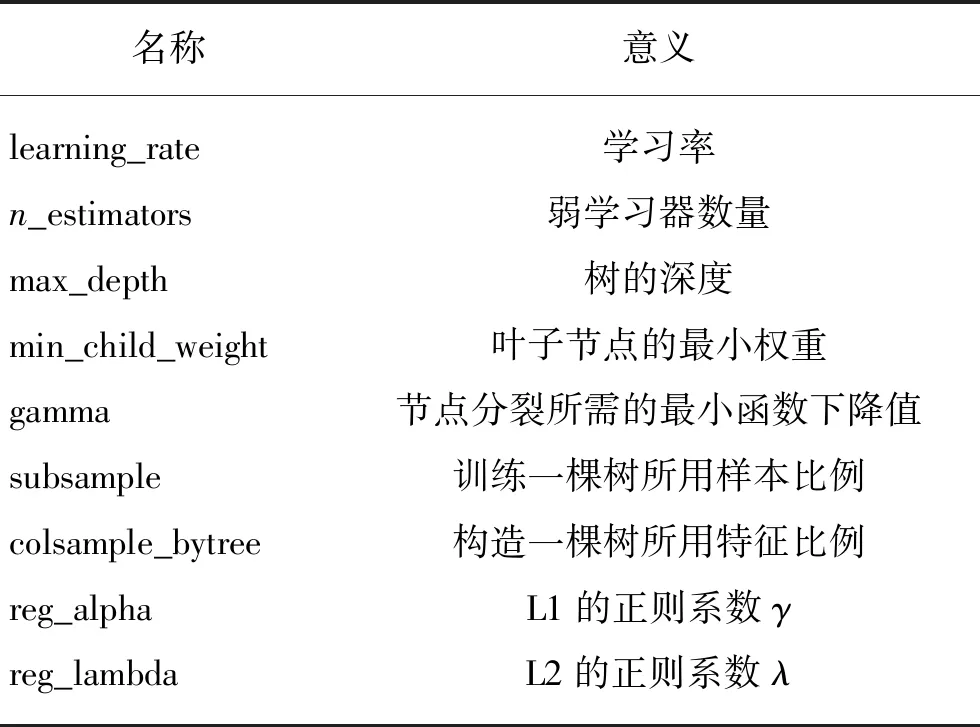
表1 主要参数

根据这些参数之间的相互关系，基于网格调参法的调参步骤见图2，首先设定学习率的值，其他参数默认，调整弱学习器数量，然后将得到的最优树的数量(n_estimators)和预设的学习率(learn_rate)固定，调整下面两个参数，以此类推，最后微调learn_rate后，得到一组优化参数。

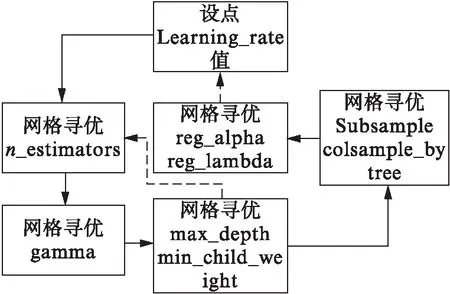
图2 参数优化

3 实验与分析

3.1 评价标准

3.1.1 混淆矩阵 混淆矩阵[14]是一个判断分类好坏程度的方法，能够轻易地辨别出每一个类别的分类状况，下面以一个二分类为例(见表2)。

表2 混淆矩阵

在表2中，真阳性(True Positive, TP)表示样本的真实类别为正例，且模型预测的结果也为正例；真阴性(True Negative, TN)表示样本的真实类别为负例，且模型将其预测成为负例；假阳性(False Positive, FP)表示样本的真实类别为负例，但模型将其预测成为正例；假阴性(False Negative, FN)表示样本的真实类别为正例，但模型将其预测成为负例。

3.1.2 Log loss函数

(6)

式中：N为样本数；M为类别数；yi,j为第i个样本是否属于第j类，是为1否为0；pi,j为第i个样本是否被预测为j，是为1，否为0。

3.2 特征提取

本文所选的振动数据全部来自于美国西储大学轴承实验数据，将采样频率为12 kHz时0.018 cm无负载的轴承数据进行小波去噪之后，将正常和各故障的原始数据分成60组，每组2 048个振动点，提取每组的时域参数：最大值、最小值、平均值、绝对平均值、标准差、峰值、方差、峭度、均方根、波形因子、峰值因子、峭度因子、脉冲因子、裕度和LBP样本熵。分别用f0，f1，…，f14对其进行标记，对应轴承的正常、滚珠故障、内圈故障、外圈故障分别标上标签L=[1,2,3]，1组数据作为1条样本，一共240条样本。

图3与图4分别为某一轴承振动数据的峭度-波形因子和峭度-脉冲因子特征参数散点图。由图可见，轴承正常状态与滚珠故障状态大部分相重合在一起，给轴承在时域的故障诊断带来了一定的困难。所以本文提出了一种基于LBP的样本熵提取方法，经实验验证该方法能有效地将轴承的正常状态与故障状态分割开来，在轴承关于时域参数的状态识别中有较好的分类效果。

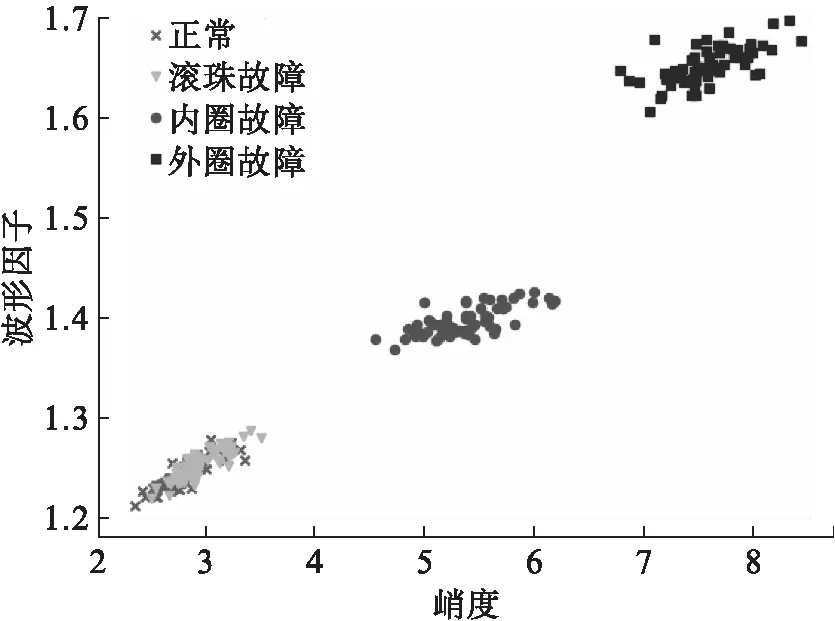
图3 峭度-波形因子散点图

图4 峭度-脉冲因子散点图

图5所示为LBP样本熵-峭度散点图。由图5可见，LBP样本熵能够轻易地将正常信号与故障信号区分开来，如果忽略横轴LBP样本熵的参与，滚珠故障和正常状态混合在一起。图6为样本熵-峭度的特征散点图，如果没有峭度的参与，内圈故障就跟正常和滚珠故障混合在一起，且滚珠故障与正常状态并没有明显的被区分出来，所以只是样本熵的参与并不会对故障的诊断起到很大的作用。

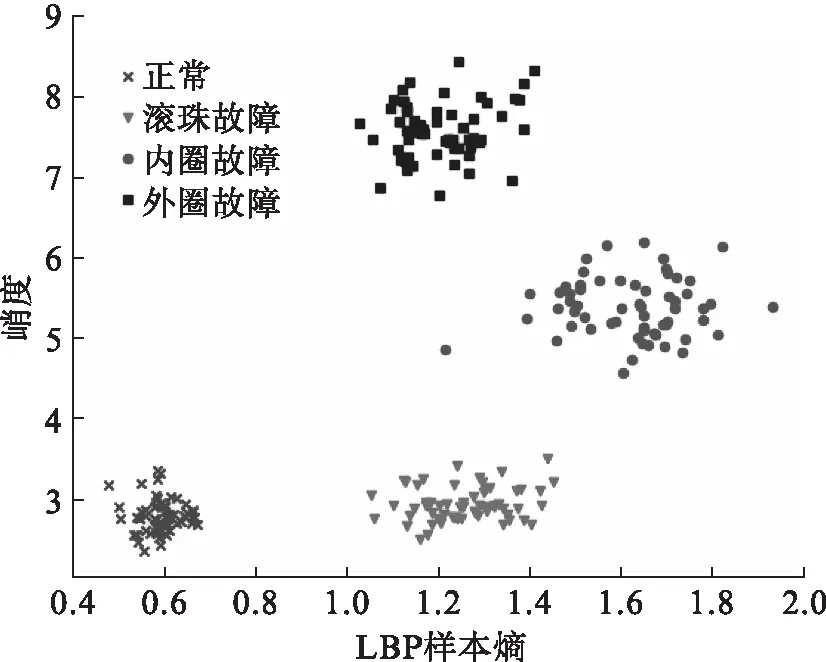
图5 LBP样本熵-峭度散点图

图6 样本熵-峭度散点图

3.3 模型对比

将所有240条样本作为XGBoost模型的输入数据，因为XGBoost为非参数模型，模型的最优参数随输入数据的不同而变化，所以本文采取网格调参[15]的方法对XGBoost模型参数寻优，获取最优参数。

为了显示LBP样本熵在时域故障诊断中的重要性，提取f0，f1，…，f13作为特征参数，按照以上的方式提取出240条样本数据，将所有样本按照5∶1的比例分成训练数据和测试数据，先用训练数据训练模型，调整参数，之后输入测试数据，得到如图7所示的预测状态与测试组实际状态相对比的混淆矩阵，横坐标为测试集上的预测，可见对于滚珠故障的预测出现偏差，一部分滚珠故障被认定为正常状态。图8所示为将f0，f1，…，f14作为特征参数时得到的混淆矩阵，与图7相比，对滚球故障的分类准确率有所提高，对其他故障的分类效果良好，可见本文所提方法相比于人工参数的分类效果良好。

图7 时域参数混淆矩阵

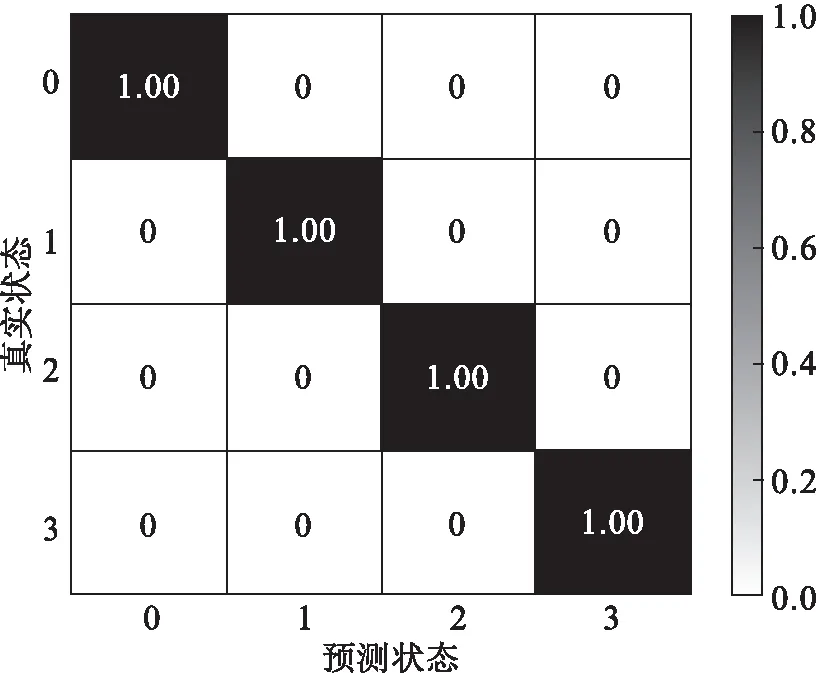
图8 LBP样本熵+时域参数混淆矩阵

为了证明本文所提方法的优越性，分别与随机森林(Random Forest, RF)、GBDT和人工神经网络(Artificial Neural Network, ANN)作对比分析，模型训练完成后，使用样本数量为160的特征矩阵测试模型效果，记录各模型的分类正确和分类错误的数量见表3，并且统计模型运行的log loss值和正确率。其中LBP训练的XGBoost模型与时域参数训练的XGBoost模型相比，分类正确数量有所提高，与其他模型相比，在正确率上有一定优势。

表3 模型对比

4 结 论

本文针对轴承各种运行状态中正常状态混杂的问题，将图像处理中的LBP算法引入到轴承的故障诊断中来，提出LBP样本熵的概念，经验证LBP样本熵能够正确地将正常状态和故障状态分离，通过XGBoost算法验证了LBP样本熵在时域故障识别中起到了一定的积极作用，将LBP样本熵与人工参数进行对比，证明LBP样本熵能够轻易地区分正常状态和故障状态。应用不同轴承不同负载的振动数据检验本文所提方法，结果证明LBP样本熵在时域故障识别中起到了一定的积极作用，与其他模型相比，LBP样本熵与XGBoost算法的结合在模型准确率上具有一定的优越性。