减小有用信号损失的BDS窄带干扰抑制技术研究
2019-11-12丁继成王奕方罗治斌
丁继成,王奕方,罗治斌
(哈尔滨工程大学 自动化学院,黑龙江 哈尔滨 150001)
0 引 言
北斗卫星导航系统(BDS)信号经过长距离的传输,到达地面接收机时的功率非常微弱,通常在-160 dBW左右,容易受到各类干扰的影响,使得接收机无法正常工作甚至直接失去解算能力.其中窄带干扰易于生成,成本低廉,干扰效果显著,因而被各类干扰设备广泛采用[1].而且随着无线电技术的发展,由无线电广播发射器产生的信号谐波等其他无意电磁干扰不断增多,其中最常见的就是窄带干扰.因此开展窄带干扰抑制技术的相关研究对我国的BDS的发展具有重要的现实意义.
基于接收机端的窄带干扰抑制技术,需要综合考虑算法的复杂度、实时性、干扰抑制能力和对真实导航信号的影响等因素.目前主要有时域抑制技术和变换域抑制技术等.文献[2]基于有线冲激响应(FIR)滤波器提出了一种变步长的窄带干扰抑制方法,引入双曲正割函数来调整步长与误差的关系,虽然收敛速度有一定提高,但是需要采用高阶滤波实现,计算量较大,当干扰数量增加或功率改变时,干扰抑制能力迅速下降;基于小波包变换的变换域算法[3]具有良好的干扰抑制效果和高精度,但算法复杂,占用资源较大,实时性不好,实际应用尚不成熟;文献[4]提出了一种基于N-sigma的频域最小均方算法(LMS)窄带干扰抑制算法,该方法有较好的抑制能力且实时性好,但是计算量大,对干扰类型敏感,而且快速傅里叶变换(FFT)与快速傅里叶逆变换(IFFT)过程中频谱泄露,栅栏效应等会对导航信号造成影响;文献[5]采用频域检测和时域陷波结合的方案对窄带干扰进行处理,利用二阶直接型陷波器对干扰进行处理,但其过渡带较宽,对干扰进行抑制的同时也去除了较多的导航信号.
针对窄带干扰信号,若干扰抑制算法对有用信号影响小,在去除干扰信号的同时保留更多的导航真实信号,则更有利于后续捕获跟踪等基带处理,可有效提高干扰抑制能力,考虑算法的综合性能,本文基于频域检测与时域无线冲激响应(IIR)陷波结合的窄带干扰抑制算法,在传统二阶直接型IIR陷波器的基础上,结合零极点配置,通过增加一对零极点改善陷波器的频率特性,复杂度低且实时性好,实现在有用信号失真较小的情况下完成窄带干扰的抑制.
1 窄带干扰抑制模型
采用将BDS接收机接收到的信号建模为
r(t)=s(t)+n(t)+j(t),
(1)
式中:s(t)为接收到的BDS信号;n(t)为高斯白噪声;j(t)为窄带干扰.BDS采用扩频通信技术,具有一定的抗干扰能力[6],当干扰超过容限时,接收机就无法正常地捕获跟踪,更无法实现精确定位、测速等功能,因此需要格外的干扰抑制模块对信号进行处理,以提高接收机的干扰抑制能力.
本文提出的时频域结合的窄带干扰抑制模型如图1所示,导航信号经量化处理后分成两路,一路进入频域干扰检测模块,选择合适的窗函数进行截断后进行FFT到频域,根据信号谱线的幅度确定干扰检测门限,从而估计出干扰信号的中心频率和干扰带宽,利用干扰参数配置IIR陷波器的系数;另一路进入时域处理模块,若检测模块判断不存在窄带干扰信号,则直接将中频信号传递到后续基带处理部分,若检测到存在窄带干扰信号,则利用配置好系数的IIR陷波器对信号进行滤波,最后得到滤除干扰后的信号进行后续的捕获、跟踪等.
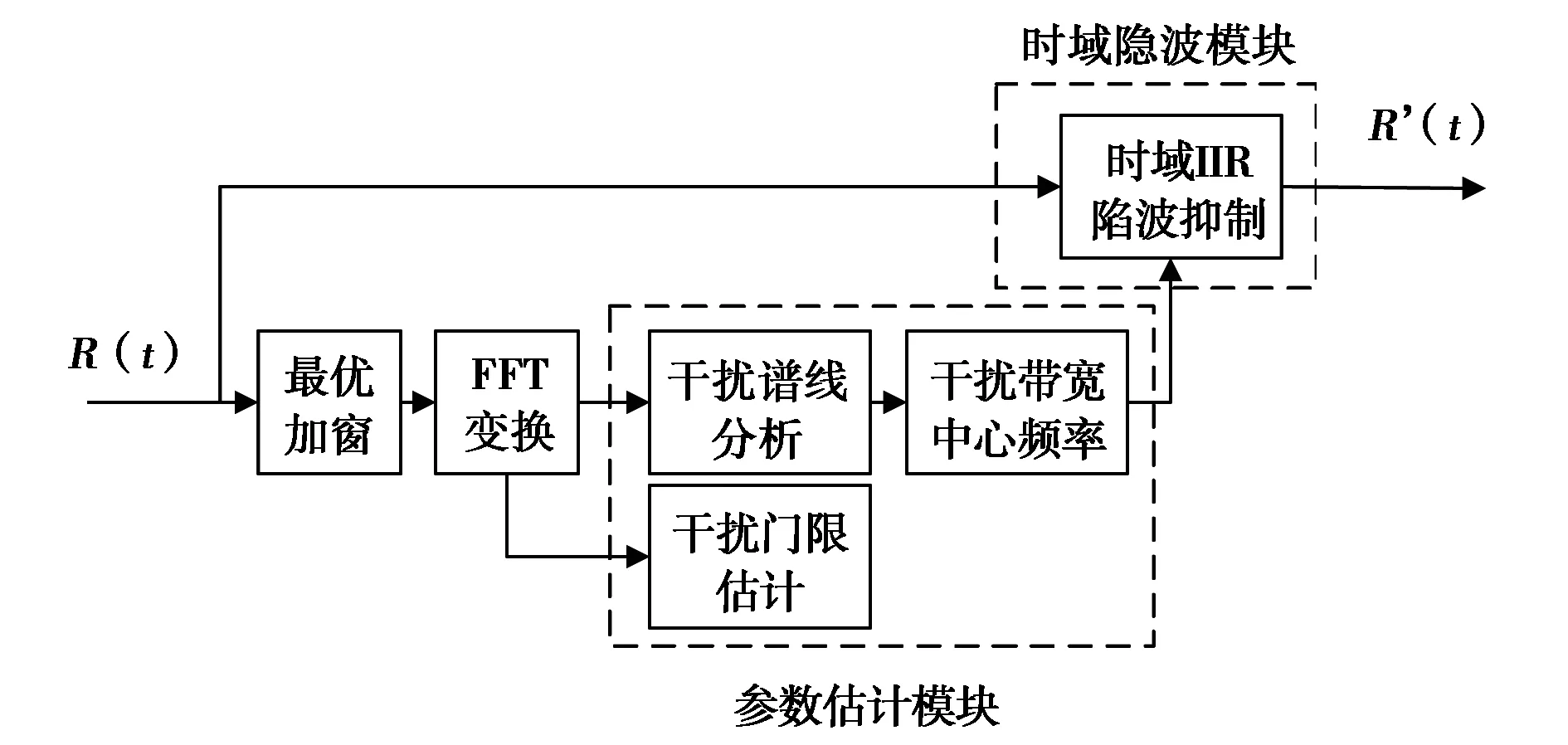
图1 时频域结合的窄带干扰抑制模型
在陷波处理过程中,时域陷波模块仅做IIR陷波,而较为复杂的陷波器参数估计过程由频域处理完成.尽管当前用于时域滤波的IIR陷波器系数是由前一时间单位接收到的数据块估计出来的,但在实际电磁环境中,干扰信号比较稳定[7],所以该方法对干扰抑制效果的影响极小.当干扰信号不稳定时,可将频域检测与时域陷波转成串行处理,即先对当前数据块进行干扰参数估计,再进行当前数据块的时域陷波.
2 窄带干扰频域检测
精确地检测窄带干扰参数是本文干扰抑制方法的重要前提.基于FFT的干扰检测算法是根据卫星导航信号功率小,频谱较为平坦,而窄带干扰在某几个频点或频带内的功率要远大于卫星导航信号,在频谱图中出现尖峰,导航信号和窄带干扰信号很容易从频域区分开.因为卫星导航信号是无限长连续信号,为了进行FFT,必须对信号进行截断,若直接截取有限个采样点会造成频谱泄露,因此需在时域选择合适的窗函数对信号进行处理[8].
不同的窗函数对信号频谱的影响不同,为了尽量减小频谱泄露的影响,一般希望具有较低的旁瓣幅度,尤其是第一旁瓣的幅度;旁瓣幅度的下降应迅速;主瓣宽度要窄,以获得较陡的过渡带,这样的窗函数处理后可以更接近信号的真实频谱.通常上述几点很难同时满足,实际选用的窗函数往往是几种条件的折中.海明窗是一种余弦窗函数,复杂度低,主瓣窄且高,能量集中在主瓣中,而旁瓣比较低,对信号的影响较小,综合性能最好,可有效减小频谱泄露,因此本文选择海明窗对信号进行加窗处理.
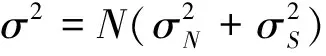
(2)
取TH=n/λ为门限值,n=1,2,3,4,5可得表1[10].

表1 谱线幅度平方分布表
如表1所示,当n=5时,即干扰检测门限TH=5/λ时,不含窄带干扰的接收信号变换到频域后,谱线的模平方大于该干扰检测门限的概率为0.006 7.在实际应用中,当FFT的点数N较大时,谱线的模平方的平均值可以作为1/λ的无偏估计.根据文献[11]中提出的λ干扰检测算法确定最终的干扰门限值,其基本步骤如下:
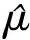
3)对N根谱线进行统计,计算|R(k)|2>TH的谱线根数,若存在|R(k)|2>TH的谱线,则将其置零,下次统计时忽略此类谱线;
4)返回第1)步,对处理之后的谱线再次进行检验,直到不存在|R(k)|2>TH的谱线为止,求得最终干扰检测门限;
5)用最终的干扰门限与所有频点的幅值作比较,高于门限值的谱线认为是干扰谱线,根据干扰谱线的分布估计干扰的中心频率和带宽.
3 二阶直接型IIR陷波器设计
在得到窄带干扰的中心频率和带宽等参数后,需要设计相应的时域陷波器对干扰进行处理.假设BDS接收机接收到的卫星导航信号中存在窄带干扰,且窄带干扰的中心频率为ω0,希望信号通过某一滤波器后能将该干扰去除掉,因此滤波器的传递函数应满足式(3),即在干扰频率处幅度响应为0,非干扰频率处幅度响应为1.

(3)
Z平面单位圆附近的零点在滤波器幅频响应的相应频率处出现凹陷,零点越靠近单位圆,凹陷越深;而Z平面单位圆附近的极点在相应频率处产生峰值,极点离单位圆越近,峰值越高[12].因此,传统的陷波滤波器设计方法是在单位圆上相应阻带位置的频率处设置零点,就可以该频率处的幅频响应为零,同时为了抵消零点引起的陷落对陷波器通带范围内幅频响应的影响,沿着极径方向放置相应的极点.为了保持陷波滤波器的稳定性,极点必须位于单位圆内,极点离单位圆越近则极点对零点的抵消作用越明显,得到的陷波器的阻带就越窄,过渡带就越陡峭.根据零极点配置方法设计的二阶直接型IIR陷波滤波器的传递函数为
(4)
式中:ZZ1、ZZ2为该陷波器的两个零点;ZP1、ZP2为该陷波器的两个极点.
令ZZ1,Z2=e±jω0,ZP1,P2=αe±jω0.
式(4)可写成
(5)
进一步简化可得
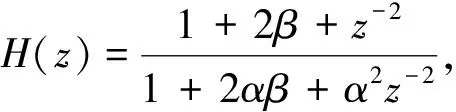
(6)
式中:α为极点结构因子;β=-cosω0,ω0为陷波器的陷波频率.
取ω0=0.2π,极点结构因子α分别为0.80与0.90,绘制对应二阶直接型IIR陷波器的频率响应如图2所示.

(a)α=0.80

(b)α=0.90
由图2可知极点结构因子α决定陷波带宽与陷波深度,即α越小,陷波带宽越宽,陷波深度越大,α越大,陷波带宽越窄,陷波深度越小.为了保持陷波滤波器的稳定性,要求极点结构因子α必须小于1.
4 陷波器的改进设计
理想的窄带干扰陷波器应该在干扰频点处的增益为0,其余频点处为1,为了尽量减少卫星导航信号的失真,陷波滤波器的陷波特性应尽量陡峭.而二阶直接型IIR陷波器的通带不对称且通带增益不确定,不满足理想窄带干扰陷波器的要求,利用这种陷波器对信号进行处理会造成有用信号失真较大,引起该缺陷的主要原因是极点在Z平面的位置不当,因此有必要选择合适的极点位置对陷波器进行改进.
Yimman等人通过修改极点位置来对陷波器进行改进,使极点对称分布在零点的两侧,用最小二乘法估计出陷波器的参数[13-14],该方法设计的陷波器可以控制通带增益,使其Nyquist频率增益与直流增益相等,确保通带及过渡带对称,其传递函数为
H(z)=b0H1(z)HADD(z),
(7)
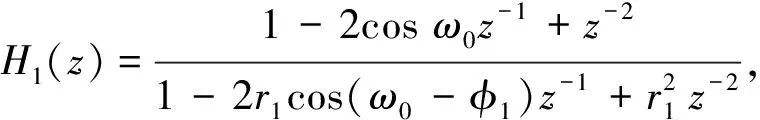
(8)
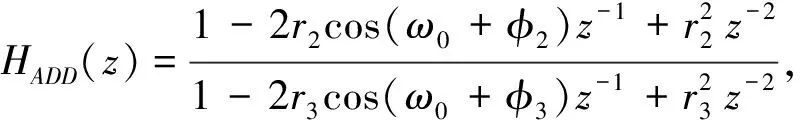
(9)
式中:φ2=0;r=r1=r2=r3;φ=φ1=φ3;
(10)
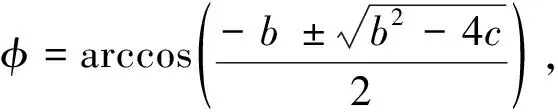
(11)

(12)
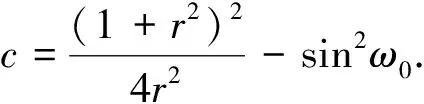
(13)
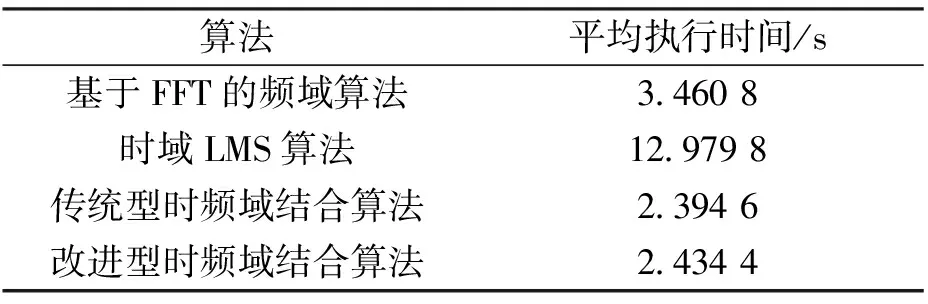
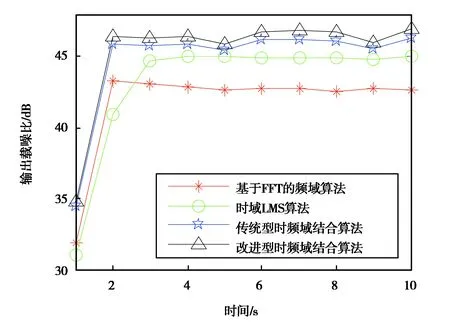
但是文献[14]只考虑了极点位置对于陷波器幅频响应的影响,下面讨论零点位置对于陷波带宽的影响.新增加的零点沿原零点极径方向放置,但二者极径不同,即φ2=0,r=r2≠1以改善幅频响应,使其对称;新增加的极点与原极点对称分布在零点的两侧,二者极径相同,即φ=φ1=φ3,r=r3,可保证两极点到零点的距离相同.由公式(5)可知,对于任意ω,其幅度响应|H(ejω)|为ejω到各零点的距离的乘积和到各极点距离的乘积之比,当r 取极点的极径r1=r3=0.80,陷波频率ω0=0.2π,分别取新增加零点极径r=0.80,r=0.77,r=0.74,并由公式(11)解得对应的φ值φ=0.186 4,φ=0.151 5,φ=0.096 5,绘制相应陷波器的幅频响应如图3.由图3可知,当r值越小,即φ值越小时,陷波带宽越窄,过渡带越陡峭.当φ=0时,求得r=0.721 6,对应的幅频如图3中实线所示,此时能得到更窄的过渡带,且通带增益可控,过渡带对称. 图3 不同零点极径对应的陷波器幅频响应 当φ=0时,基于式(11)~(13)可得 (14) 综上所述,在文献[14]的对称极点设计法基础上,选择合适的新增零点极径能得到更陡峭的过渡带,其传递函数为 H(z)=b0H1(z)HADD(z), (15) (16) (17) (18) 为验证该陷波器设计方法的有效性,基于MATLAB仿真平台,分别根据传统设计法、对称极点设计法与本文改进设计法设计陷波频率ω0=0.2π,r1=0.90的IIR陷波器,其幅频响应和相频响应如图4与图5所示. 图5 三种方法设计的陷波器相频响应 由图4可知,传统设计法的通带增益不可控,部分非陷波频率处的增益不等于1;对称极点设计法能控制通带增益且过渡带对称;采用改进设计法不仅具有上述优点,而且能取得更窄的过渡带,陷波特性更加陡峭,既可以有效地抑制窄带干扰,又能减小导航信号的失真. 但是IIR陷波器引入导航接收机的非线性相位特性可能会导致导航信号失真,抑制干扰后,接收机输出载噪比受陷波幅频特性及相位特性共同影响.由图5可以看出,改进设计法的陷波特性较陡峭时,相位特性的非线性程度大;传统设计法相频响应在阻带上非线性程度较小,但其陷波特性不如改进设计法陡峭,根据第5节的仿真实验分析不同设计法的幅频特性与相频特性对信号失真的影响. 为验证本文所提的时频域结合窄带干扰抑制算法的性能,在此进行仿真实验. 仿真条件如下:输入信号为含有高斯白噪声和窄带干扰的北斗B1I仿真中频信号,信号功率为-160 dBW,噪声功率谱密度为-205 dBW/Hz,信号带宽4.092 MHz,采样频率20 MHz,多普勒频率-1301.815 Hz,取干扰信号为双音干扰,干扰频率为3.548 MHz和4.648 MHz,干信比为30~80 dB,步进为5 dB. 基于接收机端的窄带干扰抑制技术,目前工程上常用时域LMS干扰抑制算法与基于FFT的频域干扰抑制算法,因此分别采用以下四种干扰抑制算法处理输入信号以进行性能对比,分别是:时域LMS干扰抑制算法[15],FIR滤波器阶数取30;基于FFT的频域干扰抑制算法,干扰门限的确定采用λ干扰检测算法,FFT变换的点数取1 024,干扰谱线处理采用直接置零法;基于传统二阶直接型陷波器的时频域结合法和本文提出的基于改进IIR陷波器的时频域结合法,均采用两个IIR陷波器串行级联,r1取0.95. 捕获峰噪比是捕获过程中最大相关峰值与噪声均值的比值.干扰会影响捕获过程中二维搜索空间的相关峰,甚至造成相关峰被噪声淹没,失去对相关峰的准确判定,导致捕获失败.对于相同的捕获策略,峰噪比越大意味着干扰抑制效果越好.载噪比是载波功率与噪声功率谱密度的比值(取对数),常用于表征输入信号的质量.干扰信号的存在会降低信号的载噪比,载噪比越高表示干扰抑制效果越好.因此,论文选取捕获峰噪比与跟踪输出载噪比分别从捕获和跟踪两个方面衡量算法的干扰抑制性能. 每一干信比下进行100次载噪比估计,可得到干信比与输出载噪比之间的关系如图6所示. 双音干扰的干信比为50 dB时,不同算法处理后的串行捕获和跟踪结果如表2所示. 图6 干信比与输出载噪比的关系 表2 串行捕获结果 用同一台计算机在MATLAB环境中对上述四种干扰抑制算法的执行时间进行测量,对长度为10 ms的输入信号进行处理,每种算法做100次测试,取平均值作为最终的执行时间,作为判断算法的实时性和复杂度的一项依据,如表3所示. 表3 不同算法的执行时间 由图6可知,上述四种算法均能有效地去除干扰信号,处理后的信号可以被正确捕获和跟踪.对于基于FFT的频域干扰抑制算法,输出载噪比最小,且随干信比的增大输出载噪比逐渐降低,说明该算法在去除干扰的同时对有用信号损伤较大,数据长度为10 ms时,平均执行时间为3.460 8 s,实时性和复杂度适中;对于时域LMS干扰抑制算法,输出载噪比损失较小,但由图7与表3可知,其收敛速度较慢,平均执行时间为12.979 8 s,实时性较差;时频域结合干扰抑制算法与前两种算法相比,输出载噪比和平均执行时间均有明显改善,其中改进型时频域结合算法的输出载噪比最高,当干扰信号的干信比为50 dB时,由表2与图8可知,该算法相比基于FFT的频域干扰抑制算法、时域LMS干扰抑制算法和传统型时频域结合算法,其捕获峰噪比分别提升约53.47 %、8.369 %和5.907 %,平均输出载噪比分别提升约5.147 2 dB、2.003 7 dB和0.508 6 dB,说明该算法在对窄带干扰进行有效抑制的同时减少了有用信号的损耗,虽然改进设计法的相位非线性程度略有增大,这种变化会导致信号失真,但由于其更为陡峭的陷波特性,干扰抑制效果更好,在二者的共同作用下,输出载噪比相较于传统的设计方案更高,信号失真更小.改进型时频域结合算法相对于传统型时频域结合算法平均执行时间略有增加,但增幅仅为1.662 %,仍远小于其他算法的执行时间,不影响算法的实用性和后续硬件实现. (a)未经干扰抑制处理 (b)经改进型时频域结合算法处理 图8 卫星导航信号输出载噪比(干信比=50 dB) 针对BDS接收机端的窄带干扰抑制的问题,本文提出一种基于频域检测与时域IIR陷波结合的干扰抑制方案,在传统二阶直接型IIR陷波器的基础上提出改进陷波器设计,得到了更为陡峭的带阻特性.仿真结果表明,该方案与其他干扰抑制算法相比,其干扰抑制效果好,对有用信号影响小,实时性好.仿真实验只对双音干扰的情况进行了讨论,当干扰信号为多个干扰或具有一定带宽的干扰时,采用单个陷波器无法对干扰实现有效抑制,也可通过调整极点极径r1的值和多个IIR陷波器级联的方式进行抑制,但陷波器的改进设计增加了IIR陷波器的阶数,比传统设计方法略复杂,但并不影响算法的实用性.另外,虽然IIR陷波器的相位非线性程度较小,但仍可能会使导航信号失真,因此将非线性相位的影响和补偿技术作为后续研究的重点.
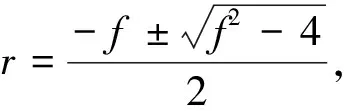
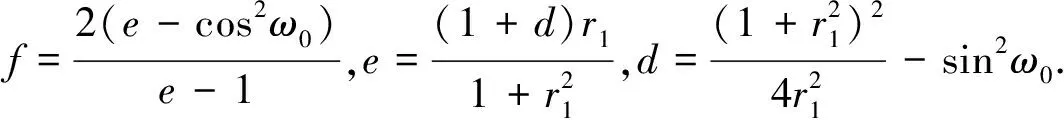
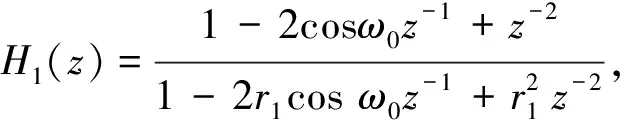
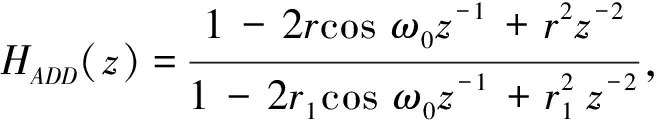

5 实验结果与分析


6 结束语
