BDS RTK/MEMS-INS组合数学模型研究与性能分析

刘崇锦,高周正,涂锐,4,张睿,韩军强,卢晓春,4

(1.中国科学院国家授时中心,陕西 西安 710600;2.中国科学院大学 电子电气与通信工程学院,北京 100049;3.中国地质大学(北京)土地科学技术学院,北京 100084;4.中国科学院精密导航定位与定时技术重点实验室,陕西 西安710600)

0 引 言

全球导航卫星导航系统(GNSS)利用卫星无线电信号进行导航、定位、授时,主要由美国GPS、俄罗斯GLONASS、中国北斗卫星导航系统(BDS)、欧盟Galileo四大全球系统和日本QZSS、印度IRNSS两大区域系统组成.BDS是中国自主研发、拥有完全知识产权、自主可控的卫星导航系统,相较于其他GNSS,采用了地球静止同步卫星(GEO),地球倾斜轨道同步卫星(IGSO)和中地轨卫星(MEO)的混合星座,并拥有短报文通信能力,其在国民经济和国防建设中扮演着重要角色.近年来,BDS发展迅速,并将于2020年前后实现全球服务[1].BDS定位精度高,精度均匀稳定,是当前主要的位置服务手段之一.实时动态载波相位差分定位(RTK)技术通过进行双差模式的基线解算,消除或减弱了钟差和大气误差的影响,可以极大提高BDS的定位精度.但BDS与其他卫星导航系统一样,有着动态性能差、数据频率低、导航信息少、抗干扰能力差的缺点.惯性导航系统(INS)技术不需要外部信息,抗干扰能力强,能提供高频、丰富、稳定的导航信息[2],但传统INS体积大,价格昂贵,难以大规模使用.自21世纪以来微机电系统(MEMS)高速发展,低成本INS的性能不断提升,使BDS+低成本INS的组合拥有了较高的实用性[3-4].两系统优劣互补,进行组合能在移动测绘、车辆导航、航空航天等领域发挥重要作用[5].因此,国内外对BDS RTK+低成本INS的组合进行了相关研究.其中,韩厚增[6]对惯导辅助下的BDS/GPS精密定位模型进行了研究;Li Wei[7]研究了车载条件下BDS RTK的模糊度固定及与INS紧组合算法;Li Tuan[4]研究分析了单频RTK与低成本INS进行紧组合的算法与性能.这些研究结果表明BDS RTK精度与GPS RTK接近,而低成本INS在BDS RTK不可用时能提供较可信的结果[6].但这些研究多集中在BDS不可用时组合导航系统的性能,而较少对BDS可用时细致的性能分析.此外,除了定位精度外,运载体的导航对速度和姿态精度也有着实际的需求[8].

因此,本文首先推导了BDS RTK与INS紧组合的量测模型与状态模型,在此基础上进行BDS+低成本INS实地跑车测试.通过对实测数据进行不同的组合模式解算,对不同组合方案的定位、测速、定姿精度进行了评价分析,并对比了各组合方案的性能.

1 BDS RTK/INS紧组合模型

BDS RTK/INS紧组合模型主要由BDS模块、INS模块、卡尔曼滤波器组成.该模型首先进行BDS、INS模块解算,再将两模块的结果输入卡尔曼滤波器进行组合,输出载体的姿态、速度、位置信息并进行反馈,完成闭环组合导航流程.其中INS模块根据惯性传感器输出的观测量δv、δθ进行INS机械编排,完成姿态、速度、位置的更新计算;BDS模块使用基站、流动站数据计算双差伪距和双差载波相位观测值,与INS推算的虚拟观测值求差,作为量测更新的新息;卡尔曼滤波模块对当前状态进行最优估计,输出改正后的姿态、速度、位置等导航参数并对惯性传感器进行反馈修正,完成闭环[9].其全过程如图1所示.

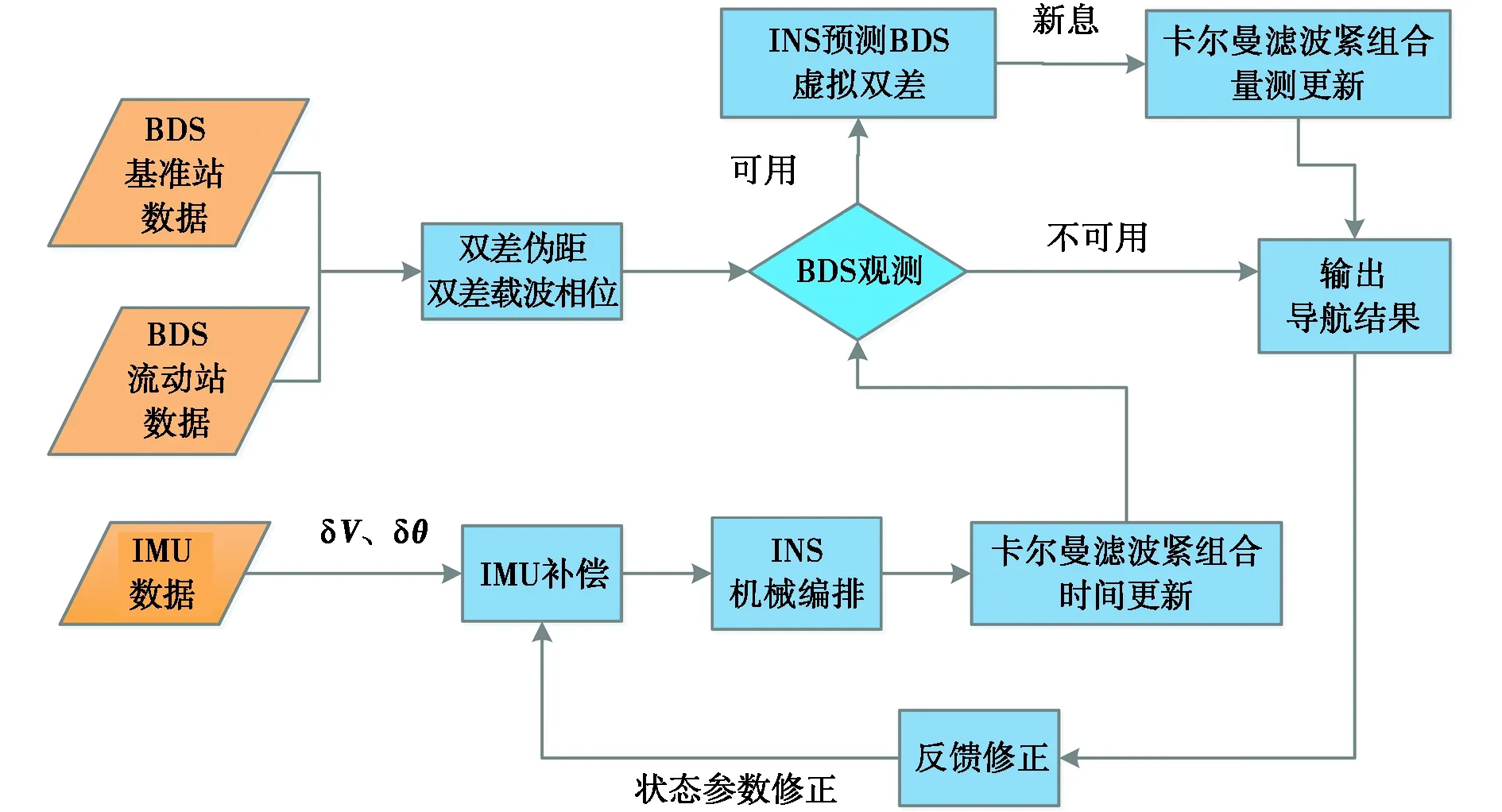
图1 BDS RTK/INS 紧组合模型

1.1 状态方程

本文采用当地直角坐标系(n系)作为参考坐标系,原点为载体中心,x轴指向地理北向,z轴向下指向参考椭球面,y轴垂直于x轴、z轴形成的平面并取右手坐标系,即北东地(N-E-D)坐标系.载体坐标系采用前右下(F-W-D)坐标系,x轴指向载体运动方向,y轴指向载体右方,z轴指向载体下方.本文是基于低精度MEMS的研究,其陀螺精度较低,无法敏感到地球自转信息,故φ角误差模型可以进行相应简化[10]:

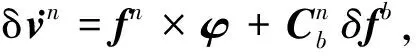
(1)

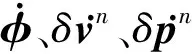
惯性传感器误差包括陀螺、加速度计的零偏误差和比例因子误差.对于低精度MEMS级别的传感器,通常采用一阶高斯-马尔科夫过程进行建模,相比与随机常值模型,可提升组合系统的抗干扰能力[8].故本文传感器误差使用如下一阶高斯-马尔科夫过程描述[11]:

(2)

式中:δb、δs为零偏误差和比例因子误差;τb、τs为零偏误差和比例因子误差的一阶高斯-马尔科夫过程相关时间;wb、ws为相应的驱动白噪声.本文所使用的陀螺和加速度计均为三轴,因此传感器误差共有12维.姿态、速度、位置误差和传感器误差构成了21维的误差状态方程:

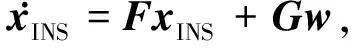
(3)

式中:F为状态转移矩阵,其形式参考文献[12];xINS为误差状态向量,其具体形式为

xINS=[δpcδvcδφδbgδbaδsgδsa]T，

(4)

G为噪声驱动矩阵;w为驱动白噪声.

在BDS RTK/INS组合中,将双差模糊度作为增广状态量,完整的状态向量为

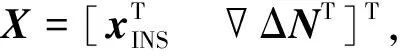
(5)

式中:xINS为误差状态向量;ΔN为双差模糊度.

1.2 量测方程

BDS RTK/INS紧组合的观测信息由实际观测的BDS双差观测值与INS预测BDS双差观测值之差构成.首先使用基站和流动站的观测数据求差,计算双差伪距、双差伪距率、双差载波相位,再与惯导推算的虚拟观测值求差,作为量测更新的观测量[13]:

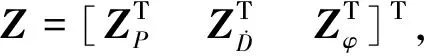
(6)

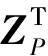
在短基线定位中,通过差分可以较好地消除对流层和电离层的影响[12],其载波相位观测方程为

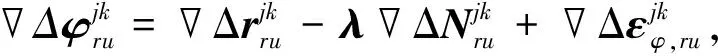
(7)

INS计算的虚拟观测距离可表示为

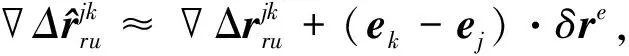
(8)

式中:ek、ej为流动站对卫星的视线向量;δre为地心地固坐标系下的位置误差向量.将式(7)和(8)相减,可得量测更新中的载波相位观测量δzφ为

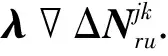
(9)

同理,伪距观测量δzp为

δzP=(ek-ej)·δre.

(10)

在接收机能接收多普勒观测值的情况下,可利用多普勒观测值构成伪距率观测量,通过与INS计算的虚拟伪距率求差,作为量测新息进行计算[14].双差伪距率量测方程为

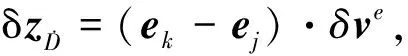
(11)

式中,δve为地心地固坐标系下的速度误差向量.

该类伟晶岩主要分布在靠近花岗岩体的变质岩中，其规模不大，多呈透镜状，其交代作用较弱，矿化较差，还可见黑云母、白云母，局部发育有绢云母化。

综合三种观测量, BDS RTK/INS紧组合的观测方程可表示为

Z=HX+V，

(12)

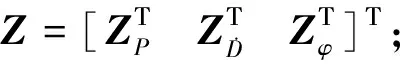
H=

其中：D为位置误差向量的设计矩阵;E为速度误差向量的设计矩阵;C1为地心地固坐标系到NED坐标系的误差转换矩阵;C2为IMU质心到BDS天线相位中心的杆臂补偿项;n为双差个数.各项详细推导计算可参考文献[13-14].

2 BDS RTK/INS组合导航系统性能分析

为评估低成本惯性器件在BDS RTK/INS组合系统中的表现,于2019年6月9日在武汉市郊进行了约40 min的跑车测试,其轨迹如图2所示.惯性器件使用某款典型的低成本MEMS-IMU,采样率为200 Hz,其主要性能如表1所示.基准站使用双频Novatel接收机,采样率为1 Hz,基线长度约为10 km.数据处理时,设置卫星高度角截止角为15°.

图2 测试轨迹图

表1 MEMS-IMU主要参数

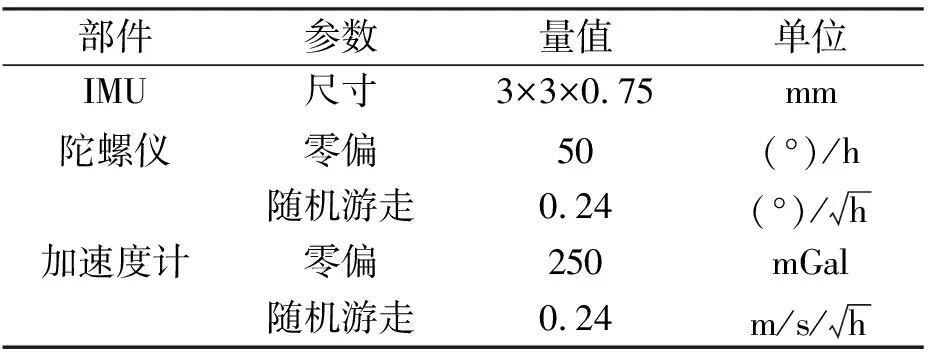
部件参数量值单位IMU陀螺仪尺寸零偏3×3×0.7550mm (°)/h随机游走0.24(°)/h加速度计零偏250mGal随机游走0.24m/s/h

图3和4表示本次实验过程中BDS可用卫星数和对应的PDOP值情况.所有历元卫星数均在4颗以上,有83.5%的历元卫星数大于8颗;99.2%的历元PDOP值小于4.说明本试验观测条件整体较好.在1587～1876 s的289个历元内,可见卫星数减少为6颗,PDOP值也大幅上升.由于该时段路径两旁有建筑物,可能形成遮挡造成可见星数下降并影响星座几何构型.

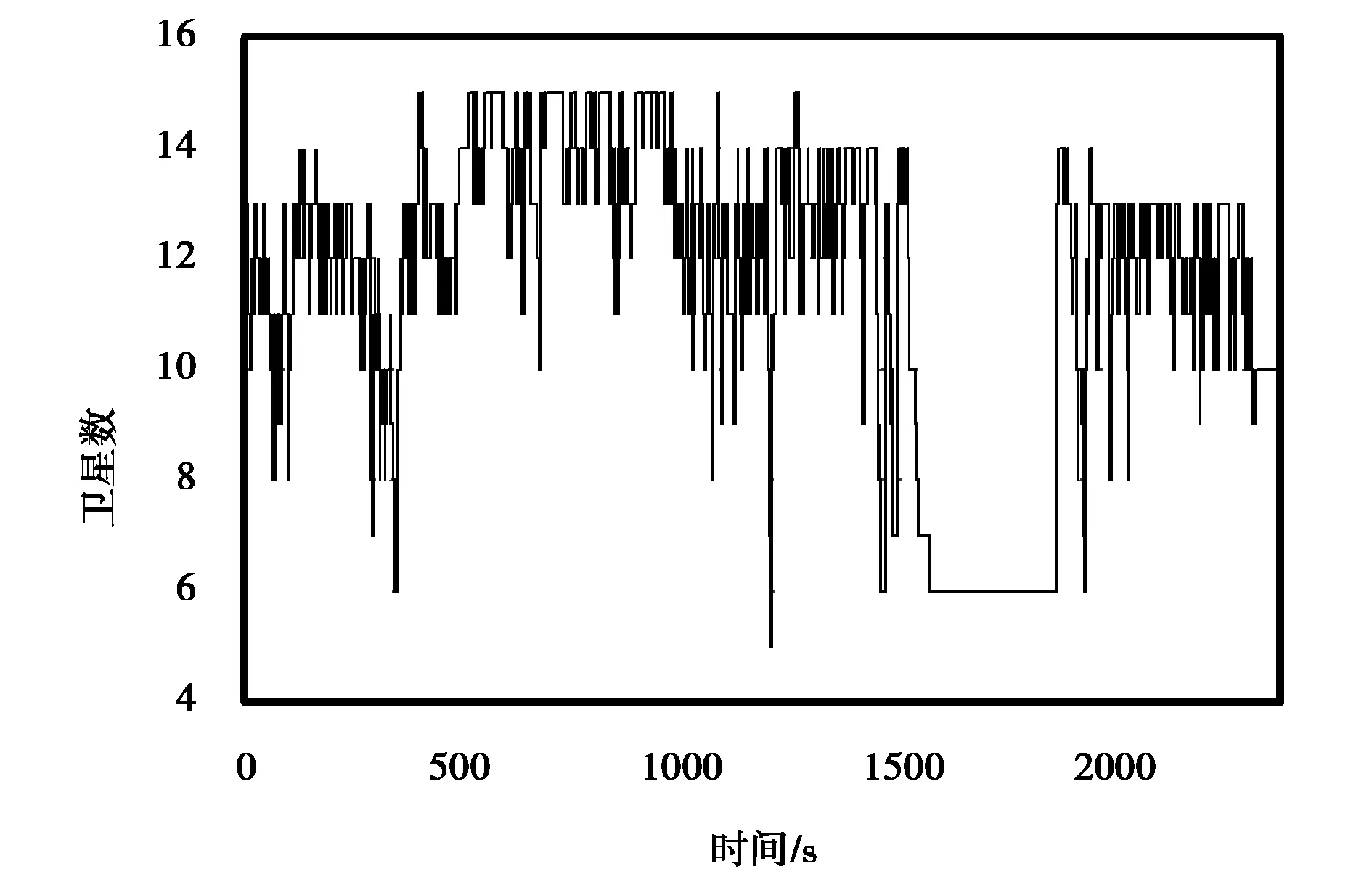
图3 观测时段卫星数

2.1 数据处理策略

本文主要测试分析正常工作情况下,低成本惯性器件(IMU)对组合导航系统的影响,故未进行信号中断测试.由于IMU精度较低,理论上在RTK级别的高精度定位中贡献较小,故主要从测速、测姿角度进行分析.本文采用的数据处理策略如下:

1)使用双频双模GNSS数据与INS数据进行双向平滑紧组合解算,作为试验的参考真值,以此为基准对组合导航系统性能进行评估.

2)分别使用BDS单频、双频数据,与INS数据进行松、紧组合解算,共有BDS单频,BDS单频松组合、BDS单频紧组合、BDS双频、BDS双频松组合、BDS双频紧组合六种组合方案,分别计算各组合导航模式的位置、速度、姿态,作为实际应用条件下BDS RTK+低成本INS组合的表现并进行后续分析.

3)将BDS单频、双频不同组合方式的实测结果与参考真值的速度、位置、姿态求差,分析不同组合方式的性能.

2.2 BDS RTK/INS定位精度分析

本试验分别使用BDS 单频、双频数据,与INS数据进行松、紧组合解算,获得相应组合方案的定位结果,再与参考值求差,评价相应组合方案的定位精度.图5、6示出了BDS单频RTK+INS的定位结果,图7、8示出了BDS双频RTK+INS的定位结果.在1587～1876 s,BDS单频RTK及BDS单频RTK松组合出现了一段时间的跳变,与卫星数及PDOP值恶化的时间段一致,故这一时段可能由于卫星数不足,卫星几何构型变差,造成定位精度下降.

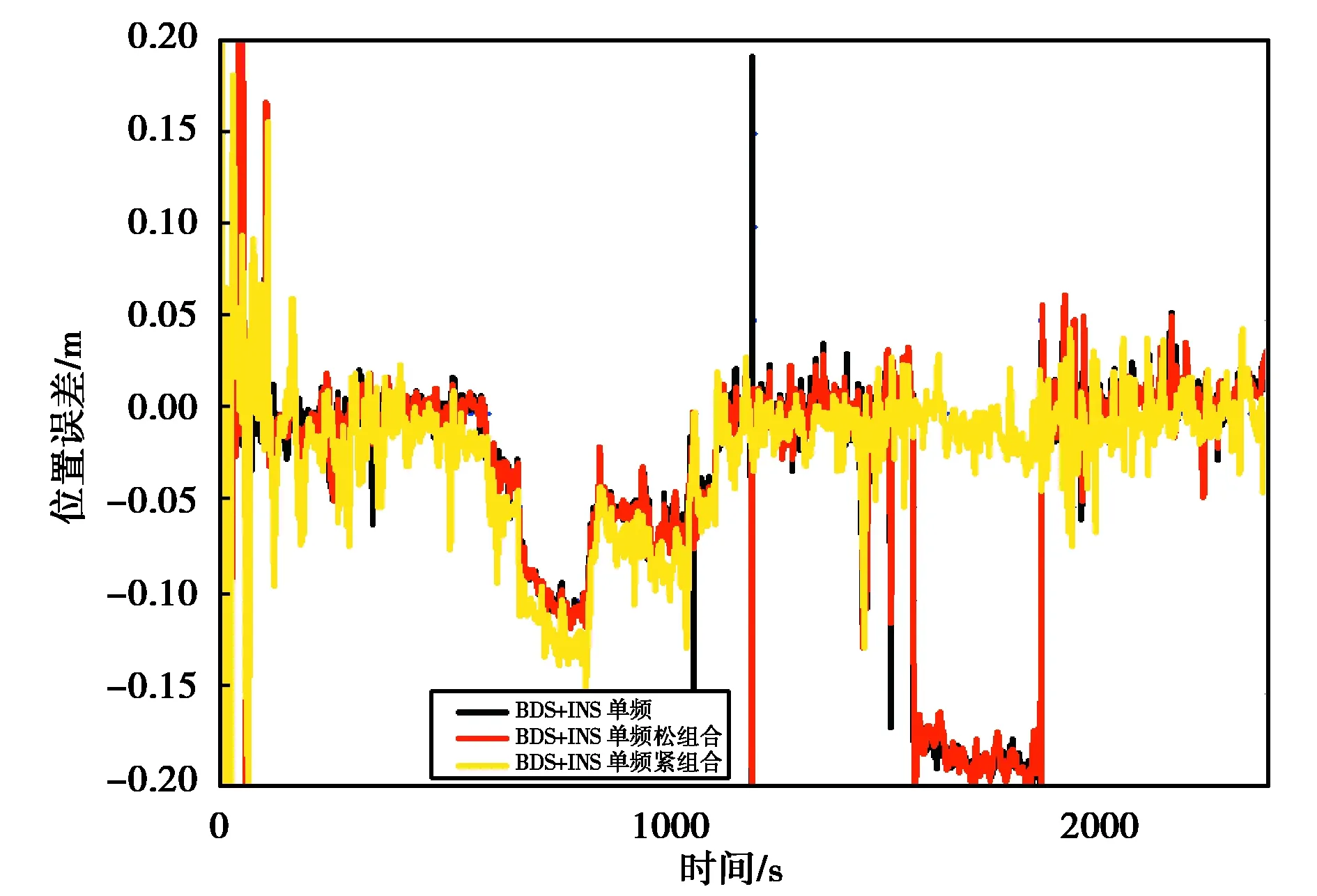
图5 单频BDS和INS融合定位东向误差

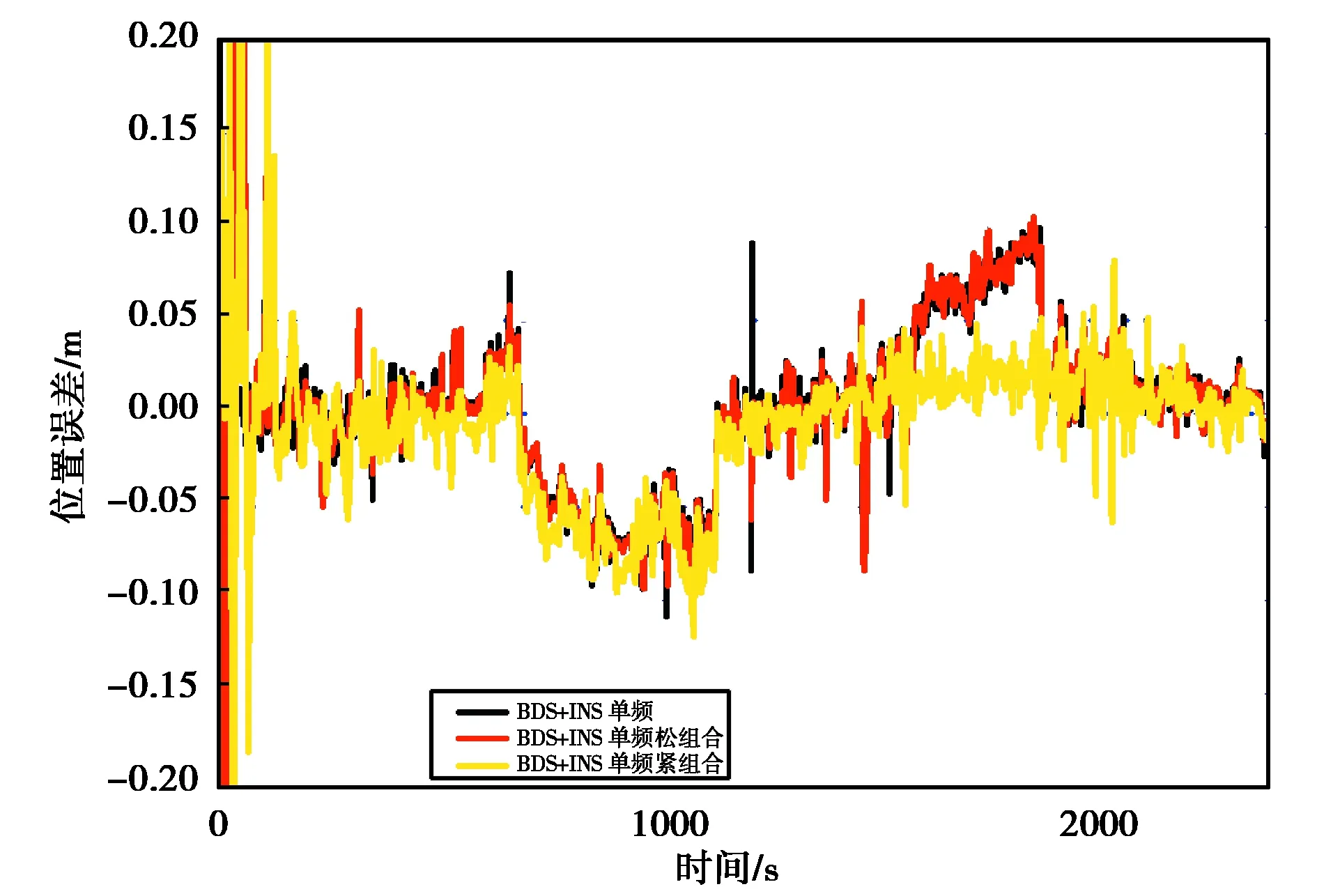
图6 单频BDS和INS融合定位北向误差

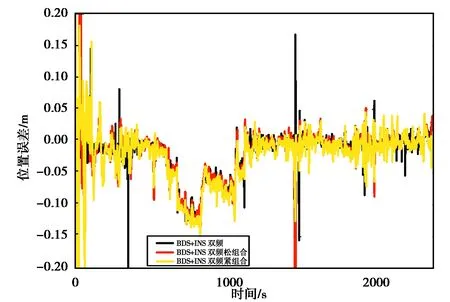
图7 双频BDS和INS融合定位东向误差

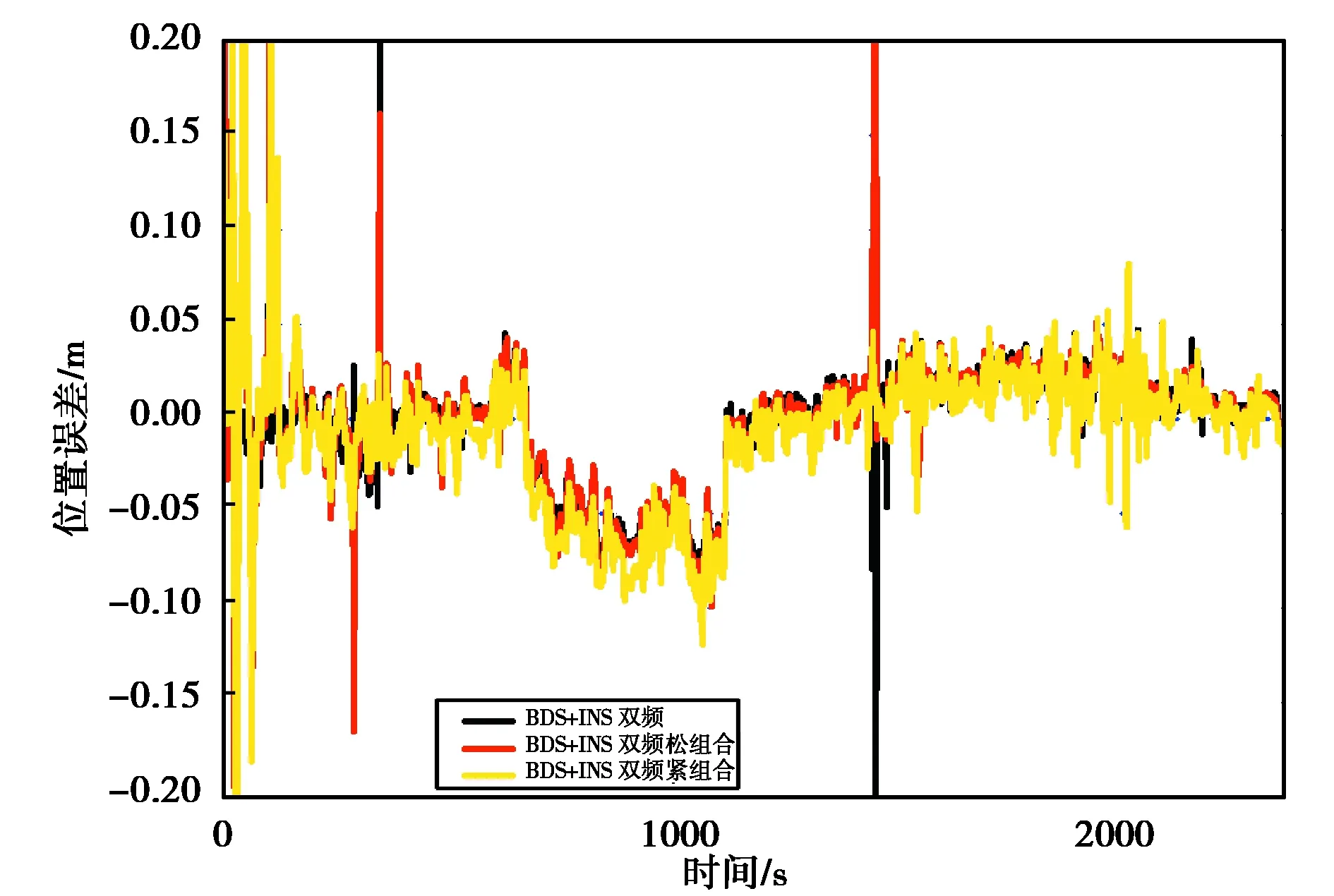
图8 双频BDS和INS融合定位北向误差

表2示出了各组合方式相对于参考值的定位误差.可以看出,当采用同一频率设置的卫星数据时,各惯导组合方式间定位精度基本相近,同一频率设置间各组合方式定位误差在mm量级,这在低成本车载导航中是可以忽略的.此外双频定位结果优于单频定位结果,在RTK、松组合、紧组合三种方案中,定位误差RMS分别在东向改善了45.9%、38.7%、42.1%;在北向改善了17.9%、10%、24.4%.此外,当出现跳变时,紧组合方式能较好地减小误差,稳定性较好,这与理论是相一致的.试验结果表明,在松、紧组合方式下,低成本IMU的引入对定位精度影响较小.

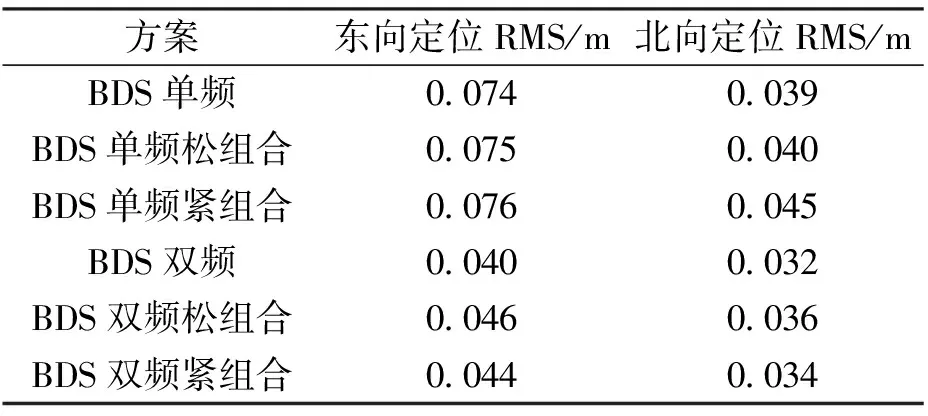
表2 不同组合方式定位精度

2.3 BDS RTK/INS测速精度分析

本试验分别使用BDS单频、双频数据,与INS数据进行松、紧组合解算,获取相应组合方式的速度,再与参考值求差,以此评价相应组合方案的测速精度.图9～11示出了BDS单频数据与INS进行组合的速度误差.在松组合模式下,相对于BDS测速,加入低成本IMU使组合系统在北、东、地方向RMS分别改善了65.9%、5.7%、57.1%.而在紧组合模式下速度精度提高更为明显,在北、东、地方向RMS分别改善了75.8%、79.5%、66.7%.图12～14示出了BDS双频数据与INS进行组合的速度误差,各组合方式的表现基本与单频一致.表3示出了BDS单双频数据与INS组合相对参考值的速度误差,可以看出即便是低精度MEMS-IMU,在与BDS组合后也能对测速精度有较大的改善.此外,单频数据+低成本INS的两种组合方式均有较好的性能,且相对双频数据差距较小,可构成单频BDS+低成本INS的低成本组合导航系统,有较高的实用价值.

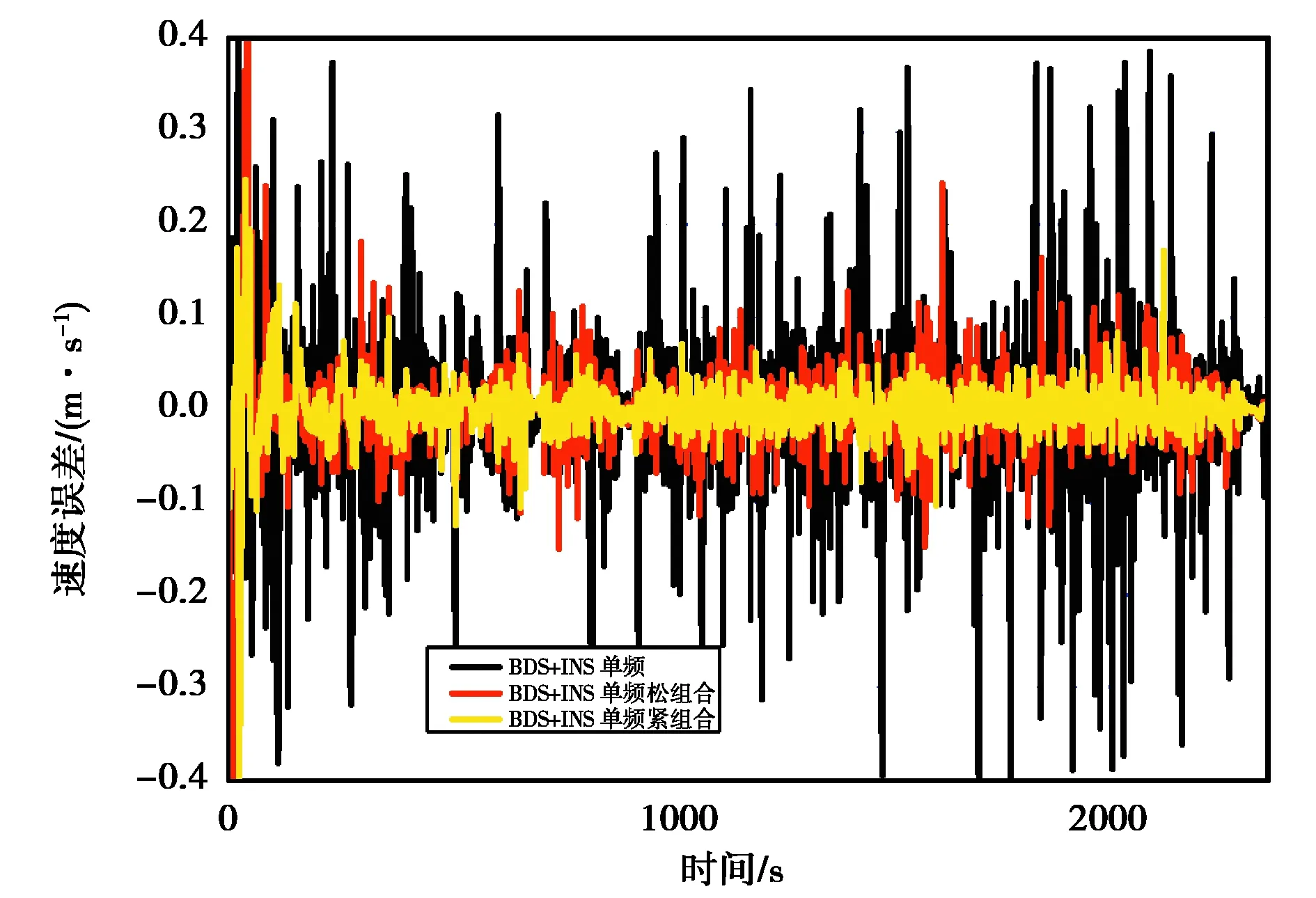
图9 单频BDS和INS融合测速N向误差

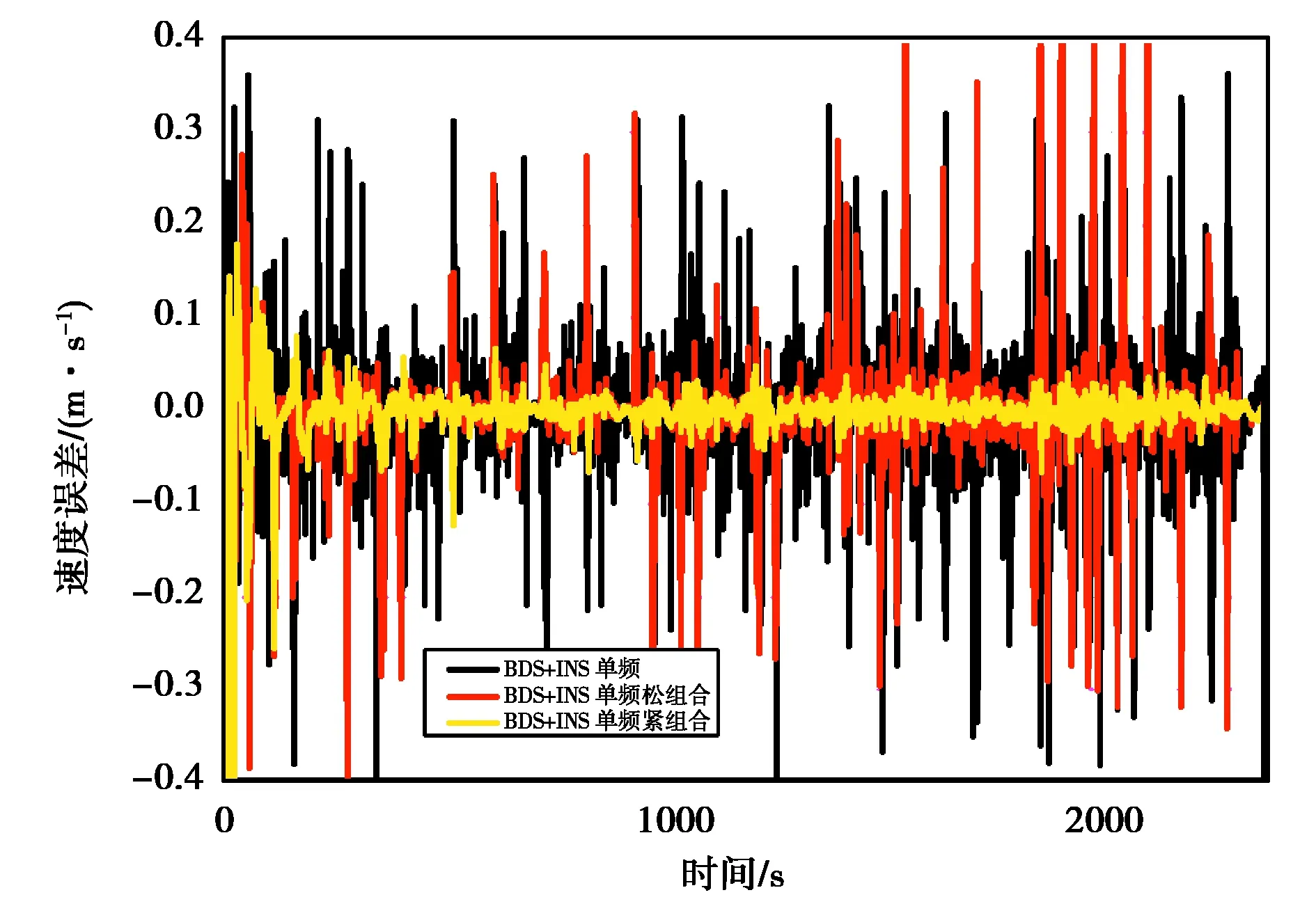
图10 单频BDS和INS融合测速E向误差

图11 单频BDS和INS融合测速D向误差

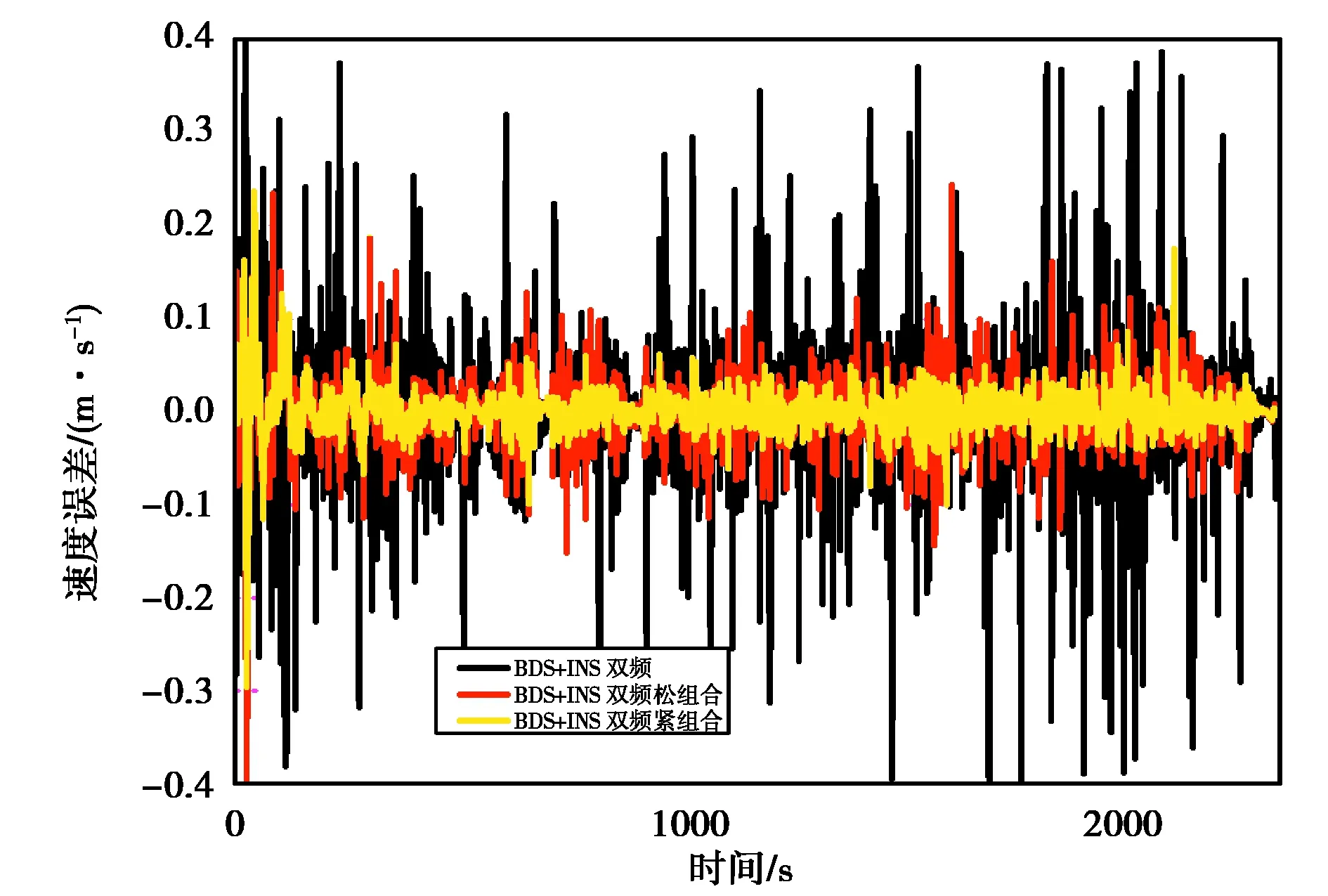
图12 双频BDS和INS融合测速N向误差

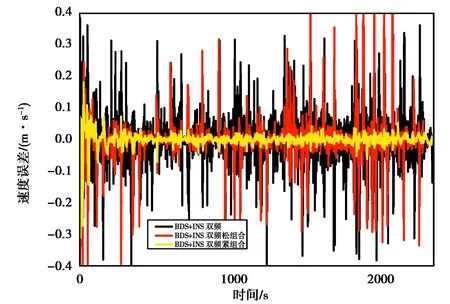
图13 双频BDS和INS融合测速E向误差

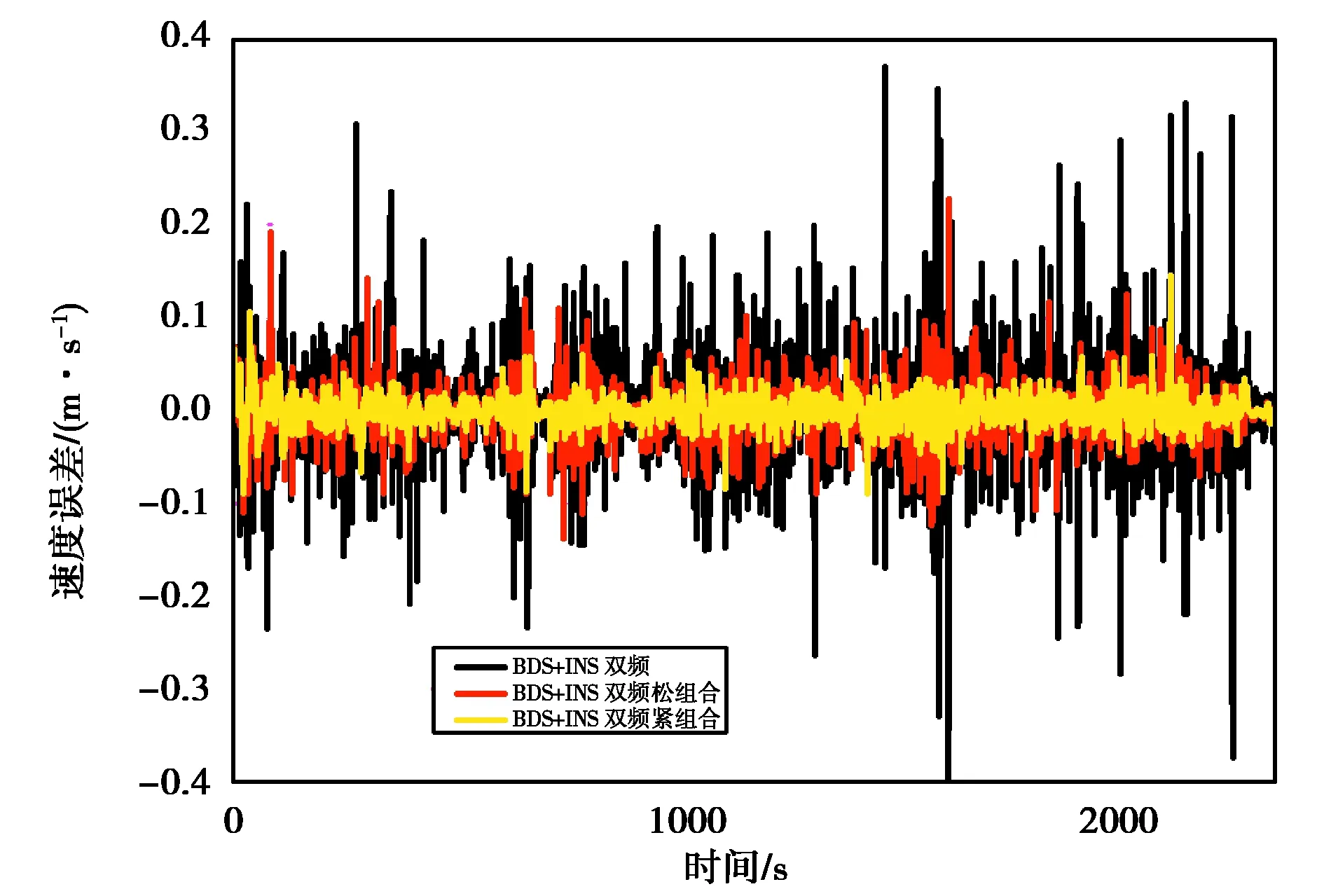
图14 双频BDS和INS融合测速D向误差

表3 不同组合方式测速精度

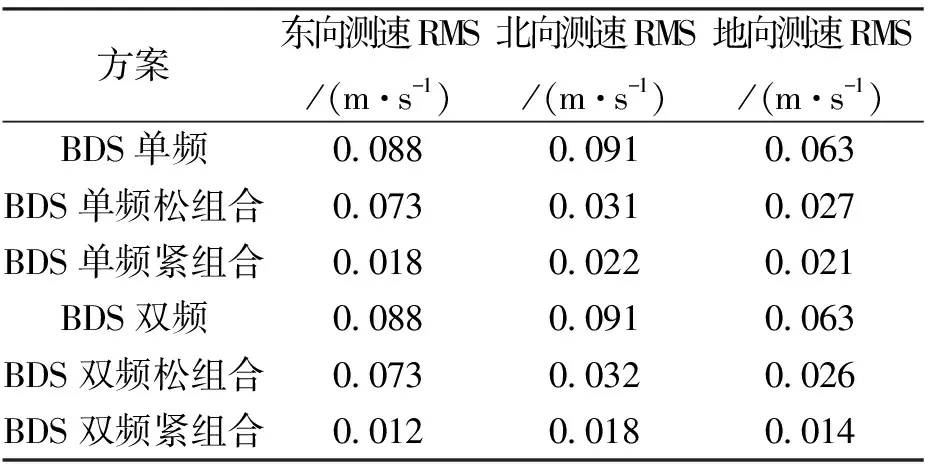
方案东向测速RMS/(m·s-1)北向测速RMS/(m·s-1)地向测速RMS/(m·s-1)BDS单频0.0880.0910.063 BDS单频松组合0.0730.0310.027 BDS单频紧组合0.0180.0220.021 BDS双频0.0880.0910.063 BDS双频松组合0.0730.0320.026 BDS双频紧组合0.0120.0180.014

在上述实验中,BDS RTK/INS紧组合模式表现出了最好的性能.为验证在此种高性能条件下BDS使用频率的影响,本试验采用BDS单频、双频数据,与INS数据进行紧导航解算,获取相应组合方式的速度,再与参考值求差,并进行对比.通过对试验结果进行分析,评价双频数据在低成本、紧组合组合导航中的实用性.图15～17示出了BDS双频数据与INS进行紧组合后的速度误差.从图上可以看出,在BDS/INS紧组合中使用双频BDS数据有效改善了测速精度,N、E、D向RMS分别改善了18.2%、33.3%、33.3%.这说明在进行BDS RTK/INS紧组合导航解算时,双频数据的引入对BDS RTK/INS紧组合导航测速精度能带来较大改善.随着电子技术的不断发展,双频芯片的成本也在不断降低,这对实现高精度低成本的组合导航系统有一定帮助.

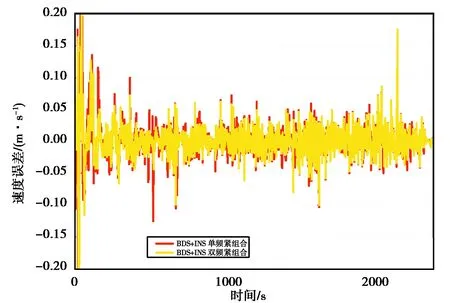
图15 单双频BDS和INS紧组合测速北向误差

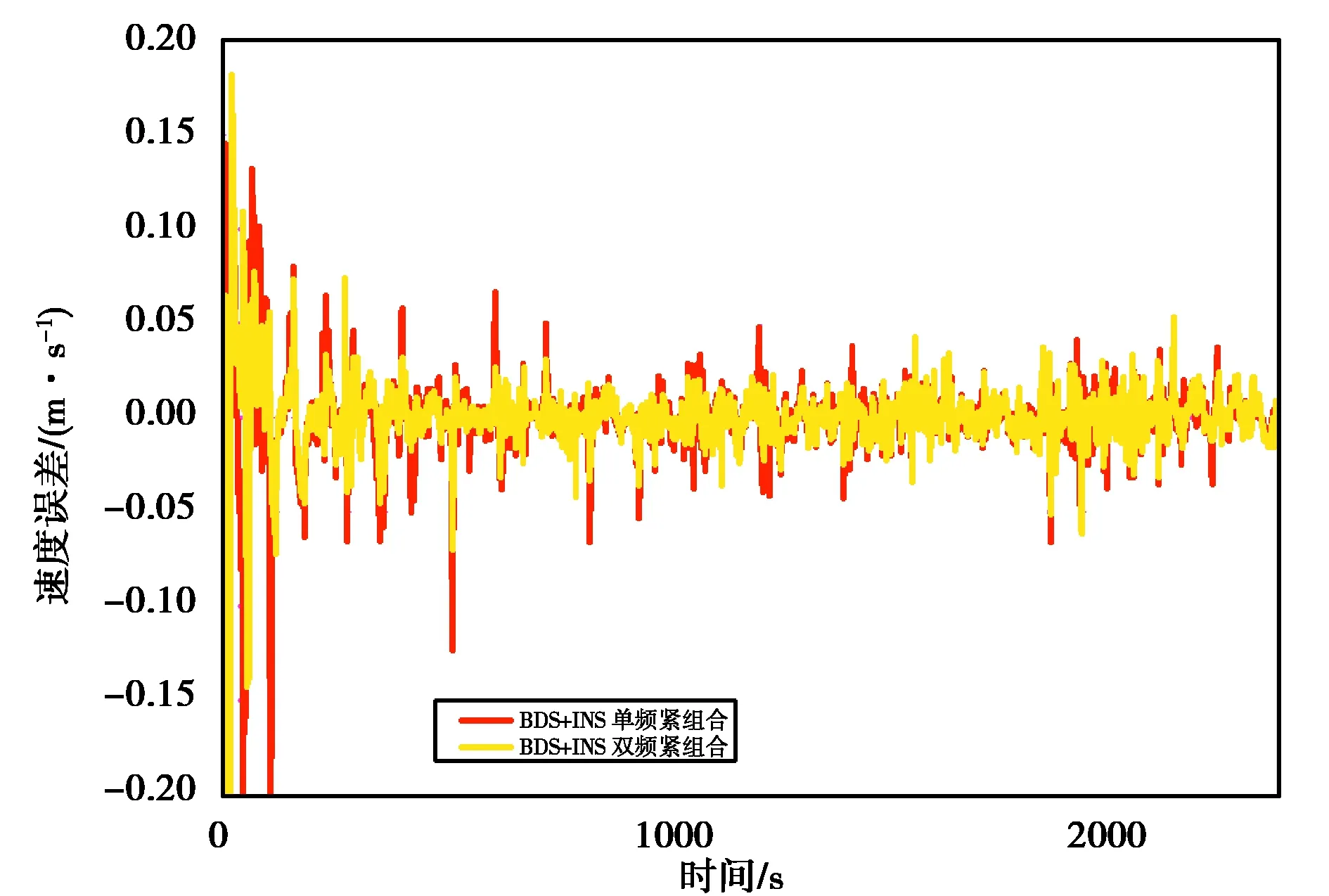
图16 单双频BDS和INS紧组合测速东向误差

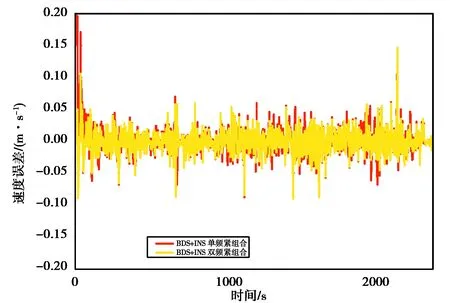
图17 单双频BDS和INS紧组合测速地向误差

图18示出了各测速方案的统计图.从图上可以看出,不论何种组合方式,低成本惯性器件的引入均能有效改善BDS的测速精度,而紧组合的改善程度较松组合更为明显.当双频数据可用时,使用双频数据能有效改善紧组合中的测速精度.

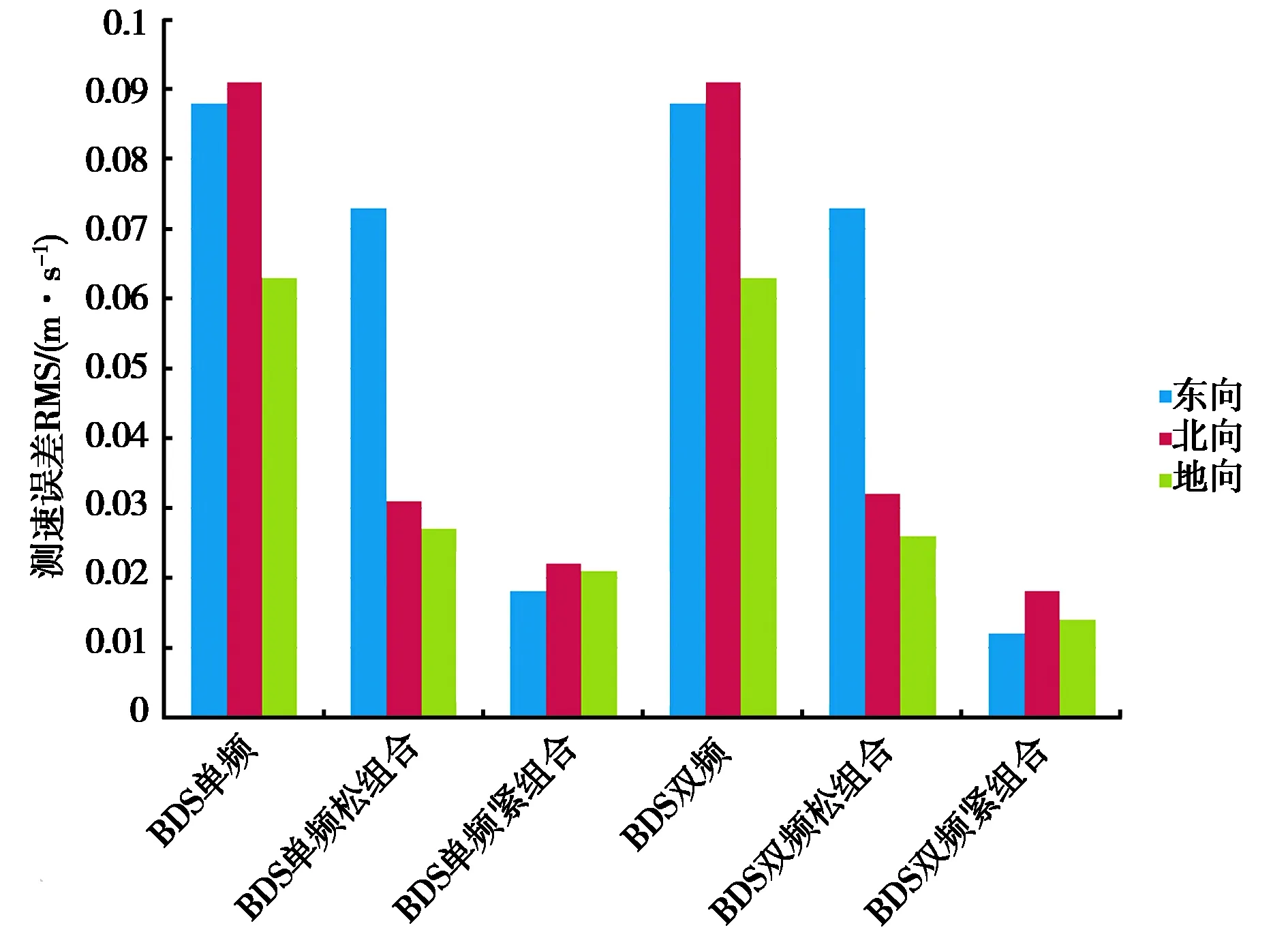
图18 不同测速方案误差统计

2.4 BDS RTK/INS定姿精度分析

本实验分别采用单频、双频BDS数据与INS数据组合解算,获取相应组合方式的姿态,并与参考值进行比较.图19～21分别示出了单、双频BDS紧组合的横滚角(roll)、俯仰角(pitch)、航向角(heading)误差.从图上可以看出,使用双频BDS数据与进行INS紧组合解算能有效减少姿态收敛时间.表4示出了两种组合方式的姿态误差RMS,使用双频数据使横滚角(roll)、俯仰角(pitch)、航向角(heading)误差RMS分别改善了41.1%、26.7%、59.0%.

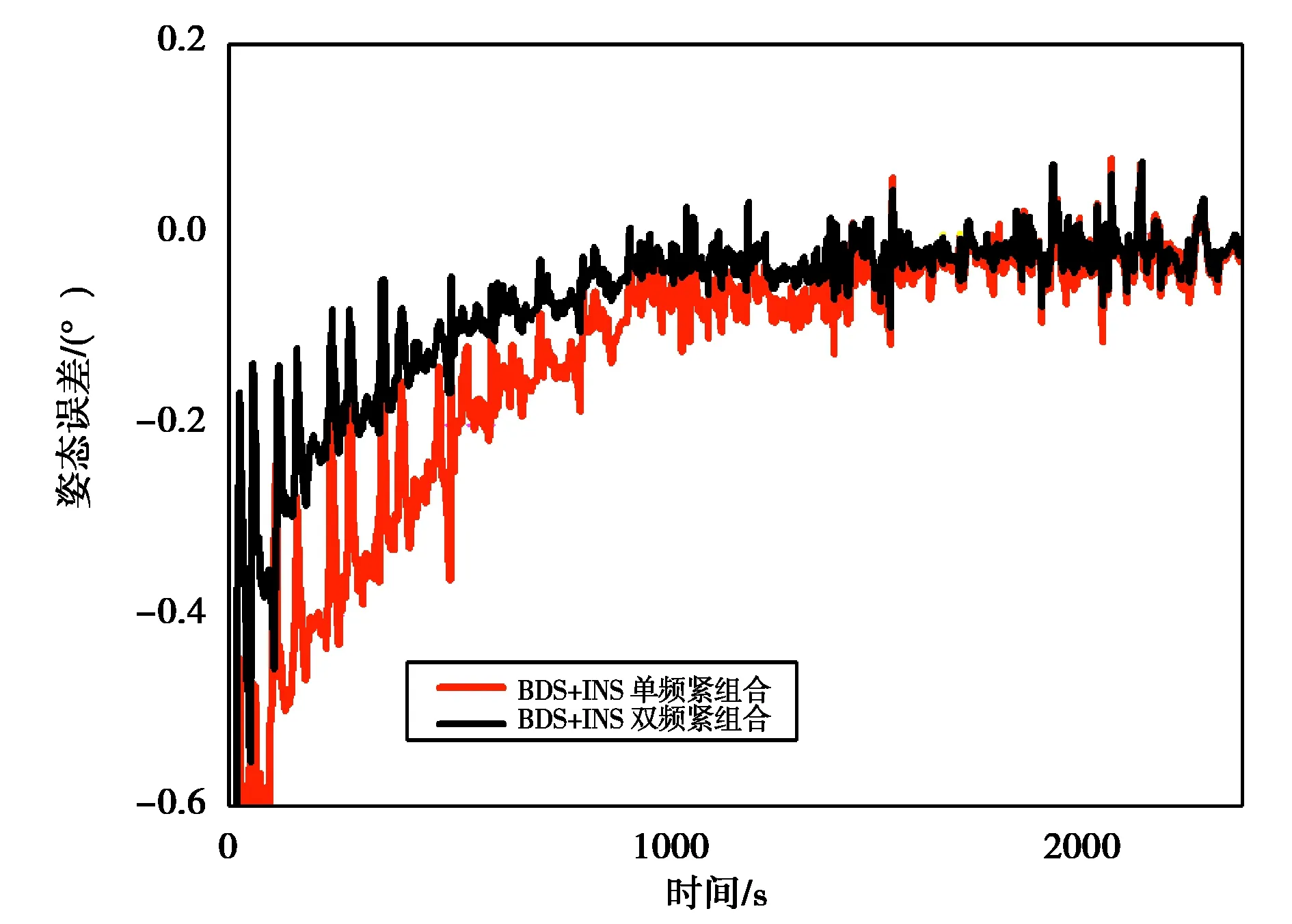
图19 单双频BDS和INS紧组合横滚角误差

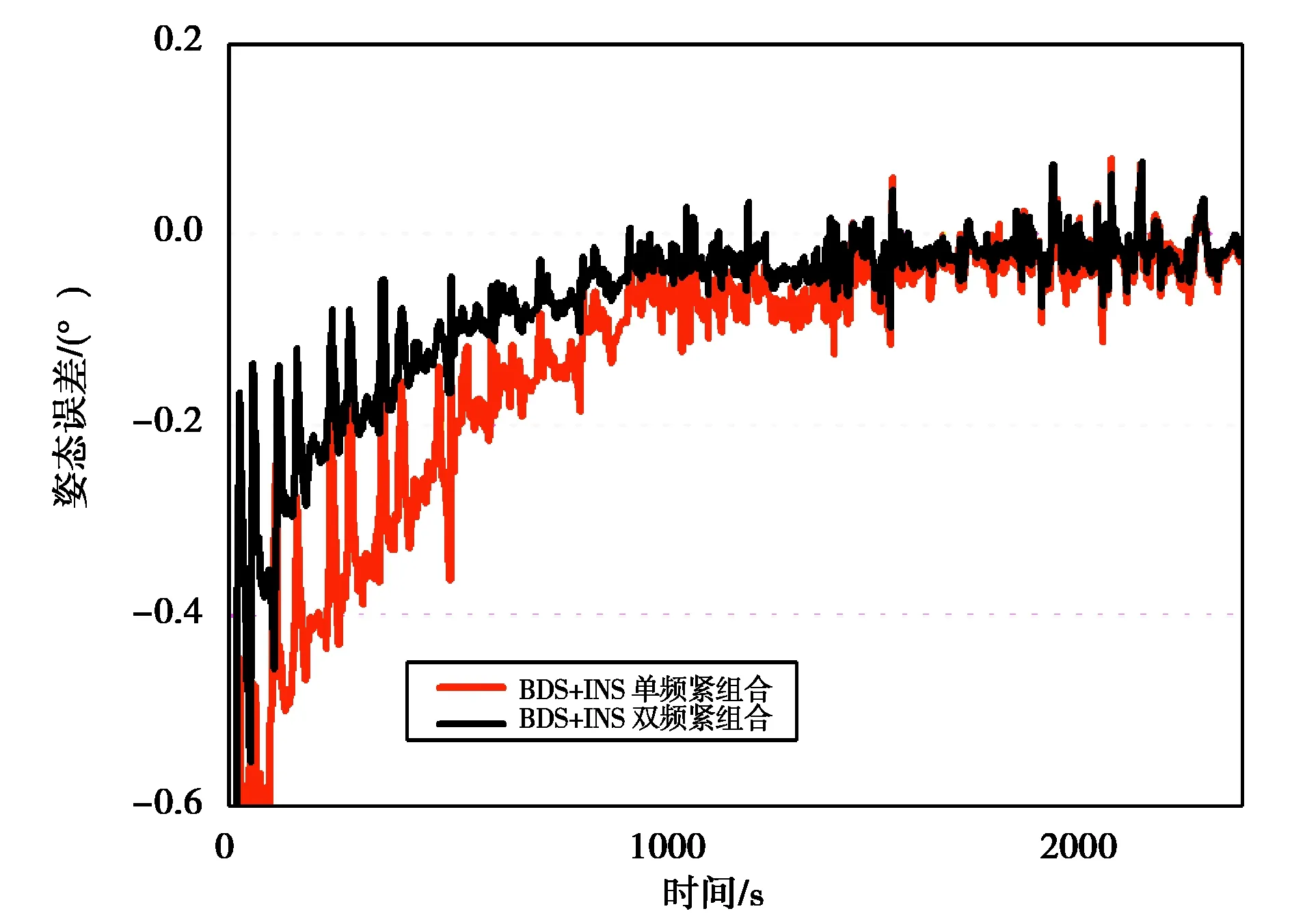
图20 单双频BDS和INS紧组合俯仰角误差

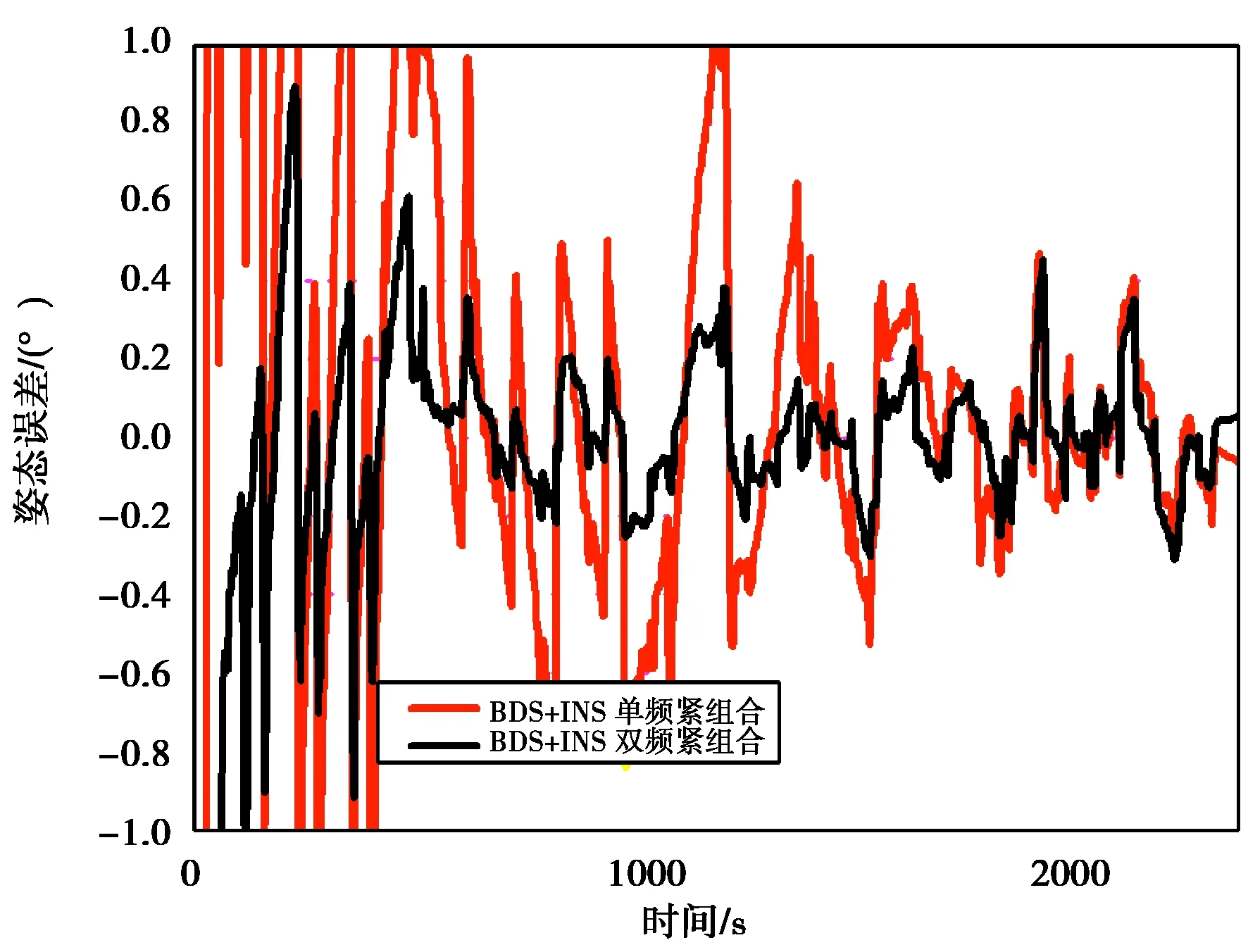
图21 单双频BDS和INS紧组合航向角误差

表4 紧组合姿态误差

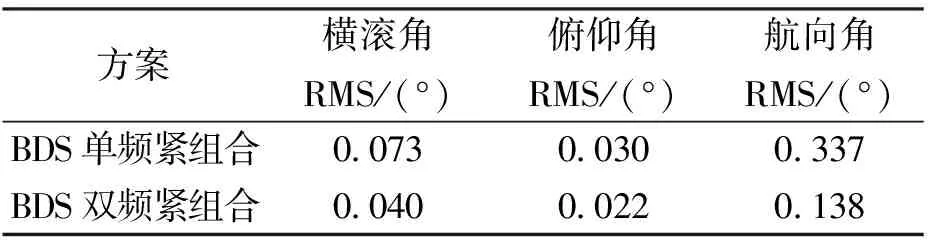
方案横滚角RMS/(°)俯仰角RMS/(°)航向角RMS/(°) BDS单频紧组合0.0730.0300.337 BDS双频紧组合0.0400.0220.138

此外,不论何种组合方式,航向角RMS明显差于其他两个方向,这可能是由于航向方向的可用性较差[9].

3 结束语

本文推导了BDS RTK/INS紧组合系统的状态模型、量测模型,并基于车载实验数据对BDS RTK/低成本INS紧组合导航系统性能进行验证和分析.实验结果表明,低成本IMU能在基本不影响组合导航系统定位精度的同时,较大改善系统测速精度.松组合模式下, N、E、D方向速度RMS分别改善了65.9%、5.7%、57.1%;而紧组合模式下速度RMS分别改善了79.5%、75.8%、66.7%.使用双频数据时,紧组合可以进一步改善系统测速精度,其N、E、D向速度RMS相对单频BDS RTK/INS紧组合分别改善了18.2%、33.3%、33.3%.而在定姿时,使用双频数据可有效减小收敛时间,改善定姿精度,使横滚角、俯仰角、航向角误差RMS分别改善了41.1%、26.7%、59.0%.

致谢:感谢武汉大学章红平教授团队提供的试验数据.