不同插值方法对GPS时间序列的影响分析
2019-11-12杨登科
杨登科
(中国铁路设计集团有限公司,天津 300142)
0 引 言
GPS时间序列中存在因突变和剔除粗差而引起的数据不连续,而快速傅里叶变换(FFT)谱分析和小波分析等要求数据均匀采样,因此在利用谱分析和小波分析对GPS时间序列进行分析时,需要对时间序列数据进行插值.
当前,国内外学者对不同插值方法对时间序列的影响进行了对比分析.如李靖[1]对比了最邻近插值、三次多项式插值、三次样条插值对GPS坐标时间序列的插值效果,并得出三次多项式插值效果最好的结论;田慧[2]利用拉格朗日、三次样条和正交多项式拟合三种插值方法对缺失点进行插值,结果表明:拉格朗日和三次样条插值方法适合缺失点较少的情况,而正交多项式可用于缺值点较多的情况;武艳强等[3]提出了多点三次样条插值的方法,在一定条件下可以解决时间序列中较多数据的缺失问题;张恒璟等[4]采用正交多项式作最小二乘拟合插补缺值点,与三次样条插值效果对比,并得出三次样条插值当缺失历元较多时易发生扭曲,高次正交多项式拟合易发生扰动,一般二次或三次即可达到很好拟合效果的结论.由于缺乏对各种插值方法系统详尽的对比分析,并欠缺对GPS坐标时间序列建模插值方法的研究,因此对GPS坐标时间序列建模插值及各种常用插值方法的插值效果及适用范围进行研究极为必要.
本文的研究目的在于利用缺值不同的GPS时间序列,采用多种类的插值方法研究不同插值方法对GPS时间序列的影响,并就其插值效果进行分析,从而得出有意义的结论.
1 GPS数据介绍及数据分析
1.1 数据介绍
本文使用斯克里普斯轨道和永久阵列中心(SOPAC)提供的7个数据完整性较好的IGS基准站2001.0014-2005.9986的坐标时间序列,并按照缺值情况分为以下6种方案:
方案1:连续缺值1、2、3、4、5个,对应缺值较少的情况;
方案2:连续缺值15个(半个月);
方案3:连续缺值30个(一个月);
方案4:连续缺值60个(两个月);
方案5:连续缺值90个(三个月);
方案6:连续缺值180个(约半年).
各IGS基准站时间序列相关信息如表1所示.
1.2 插值方法介绍
选择最邻近插值、线性插值、三次多项式插值、三次样条插值、拉格朗日插值和建模插值共6种插值方法对GPS时间序列进行插值,并就拟合效果进行对比分析.其中最邻近插值、线性插值、三次多项式插值、三次样条插值和拉格朗日插值方法均为较为常用的数据插补方法,这里就不再详细论述其原理.现将建模插值方法进行简要介绍.
通过对GPS时间序列建立如式(1)所示的参数模型[5],以达到插值的目的.
y(ti)=a+bti+csin(2πti)+dcos(2πti)+
H(ti-Thj)+vti,
(1)
式中:ti为GPS站点单日历元,以年为单位;a为横轴截距;b为线速度;c、d和e、f分别表示年周期和半年周期项的系数;gi表示跳变振幅;Thj表示发生跳变的历元;n为跳变个数,H为Heaviside阶梯函数,在发生跳变前H值为0,跳变后H值为1;vti为观测噪声.
2 不同插值方法效果比较
利用1.1节中的6种方案和1.2节中的插值方法,对选取的7个IGS基准站坐标时间序列进行插值,将拟合值与真值进行对比,并取其差值的均方根(RMS)作为评判标准.
1)方案1
此方案针对缺值较少的情况(1~5个),各插值方法的插值效果如表2所示,限于篇幅,仅显示N、U方向的拟合效果.
表2 方案1不同缺值情况下各插值方法的均方根mm
由表2可知,当缺值较少时,最邻近插值、线性插值、三次多项式插值和建模插值效果相当,但在N方向最邻近插值效果较差,建模插值效果最好,U方向线性插值和三次多项式插值效果较好;三次样条插值仅适用于缺值偏少的情况(如1,2,3,4),但插值效果并不理想;拉格朗日插值效果最差,其均方根在每个缺值阶段均很大,且随着缺值数量的增多而增大.
限于篇幅,此方案中仅列出BOR1站连续缺值5个点的插值结果图,如图1所示(因拉格朗日插值效果太差,未显示).

图1 连续缺值5个点插值结果图
由图1可知,当缺值数量为5时,三次样条插值方法拟合值偏离真值较远,插值效果较差;其余插值方法拟合值均在真值附近,插值效果相当.
2)方案2~6
针对缺值较多的情况,缺值个数为15、30、60、90和180,对应时间分别为半个月、一个月、两个月、三个月及半年.不同缺值情况下各插值方法的均方根如表3所示.
表3 方案2~6不同缺值情况下各插值方法的均方根mm

缺值最邻近NU线性NU三次多项式NU建模NU三次样条NU拉格朗日NU151.46.91.35.71.46.21.25.64.219.1479411842 301.46.81.45.61.46.71.24.96.930.11078791034038 601.97.71.76.21.86.61.25.111.764.672548187166459768 901.99.21.48.81.99.71.35.521.2113.5213217401013780743799 1802.39.61.48.62.28.81.35.839.6213.914782444021913214512130662
由表3可知,当缺值数据量逐步增大时,最邻近插值、线性插值和三次多项式插值效果逐渐变差;在每个缺值阶段,建模插值效果均最好;三次样条插值和拉格朗日插值效果最差,且有随着缺值数量增多均方根逐步增大的趋势.
限于篇幅,此方案中仅列出BOR1站连续缺值180个点的插值结果图,如图2所示(因三次样条和拉格朗日插值效果太差,未显示).
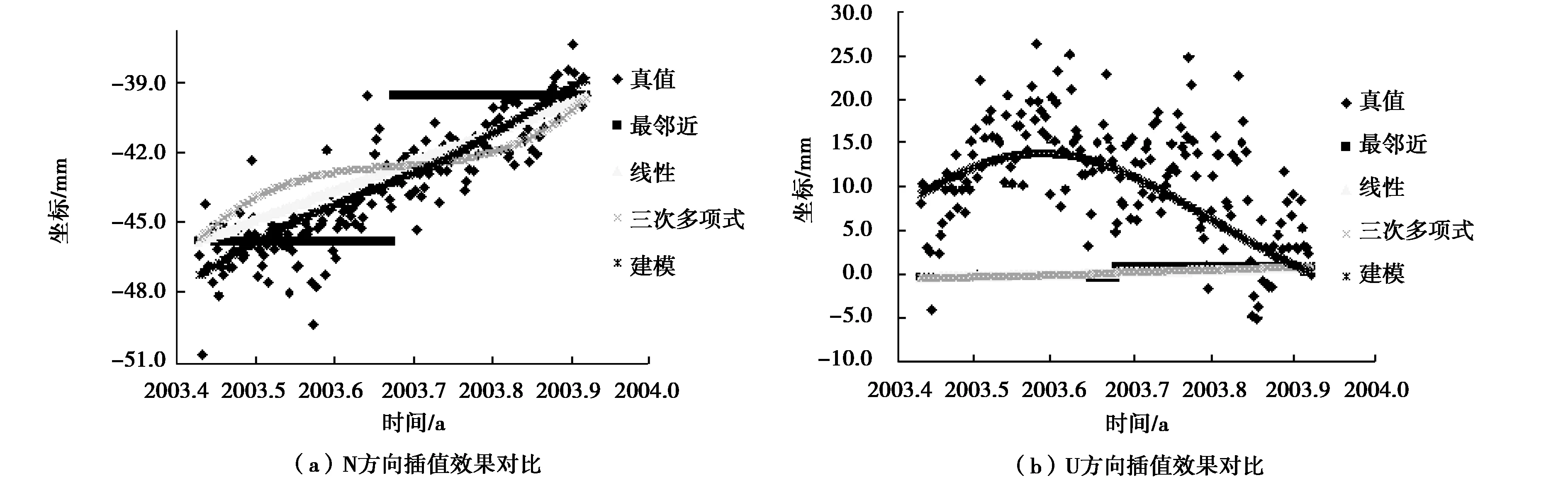
图2 连续缺值180个点插值结果图
由图2可知,当缺值数量为180时,建模插值与真值最为接近,为最佳插值方法,其余方法插值效果较差,U方向尤为明显.
3 结束语
随着GPS的快速发展,怎样从大量观测数据中提取那些与地球物理现象有关的信息,已成为GPS时间序列研究的热点问题,而谱分析和小波分析等却需要对残缺的时间序列数据进行插值,因此进行GPS时间序列的插值研究极为必要[15].本文通过对7个IGS基准站在不同缺值情况下的坐标时间序列进行插值分析,得出以下结论:三次样条插值和拉格朗日插值效果较差,在每个缺值阶段其均方根均较大,且有随着缺值数量增多而增大的趋势;最邻近插值、线性插值和三次多项式插值仅适用于缺值较少的情况;建模插值在每个缺值阶段的插值效果均较好,且随着缺值数量的增加,这种优势更为明显.
