CME对IGS基准站坐标序列噪声模型及速度估计影响分析
2019-11-12马飞虎岳祥楠贺小星金依辰
马飞虎,岳祥楠,2,贺小星,2,金依辰
(1.华东交通大学 土木建筑学院,江西 南昌 330013;2.轨道交通工程信息化国家重点实验室(中铁一院), 陕西 西安 710043)
0 引 言
已有研究表明IGS基准站坐标时间序列中不仅包含构造运动信息,也包含非构造运动引起的时空相关噪声,国内外学者将这种时空相关的噪声称为共模噪声(CME),并指出共模误差是IGS基准站坐标时间序列程序周期性的主要原因之一[1-4].
针对共模误差的时空特性及其影响是当前研究的热点.常金龙等对大华北GPS时间序列共模误差进行剔除,采用Stacking+主成分分析(PCA)方法,结果表明小区域GPS时间序列中包含的共模误差比大区域的成分多,扣除随机噪声试验说明并非用任意噪声序列都能起到共模误差滤波的作用[5].王健等[6]利用叠加滤波、PCA及KLE 3种方法对欧洲区域平均基线长度为2 000 km的大空间GPS网12个站进行分析,对比3种方法剔除共模误差的效果,结果显示对于较大的GPS观测网,相对于叠加滤波,PCA及KLE法效果更好并能显示不同站点的空间特征.贺小星等[7]提出了一种依据地理环境因素且多尺度评价体系的GPS时间序列广义共模误差分离方法,实验结果表明广义共模误差分离方法获得了更好的滤波效果,提高了坐标序列的精度并克服了传统GPS基准站坐标时间序列模型的局限性.明锋等[8]将PCA结合独立分量分析(ICA)进行提取共模误差,采用模拟数据对ICA提取CME的精确性和有效性进行验证,并与PCA结果进行对比,结果表明ICA能够有效地提取观测网CME,但具有一定局限性.然而,CME是否会对较长时间的IGS基准站运动特征产生相关的影响,如对IGS基准站速度估计、周年振幅等的影响,有待进一步研究.
本文以连续运行GPS观测站坐标序列为研究对象,利用贝叶斯信息量准则模型估计方法,对幂律噪声+白噪声(PL+WN)、白噪声+闪烁噪声(FN+WN)、闪烁噪声+随机游走噪声(FN+RW)、白噪声+随机游走噪声+闪烁噪声 (FN+RW+WN)四种噪声模型进行分析,探讨CME对噪声模型建立及其站速度估计的影响.
1 GPS数据及处理方法
1.1 GPS数据
IGS数据中心提供了全球连续观测基准站坐标时间序列,为研究地壳运动的时-空变化规律、构造变形的三维精细特征等科学问题提供基础资料和产品[9].本文对50个长周期的IGS基准站的坐标序列进行研究,所选的IGS基准站坐标序列时间跨度信息如图1所示.从图1可知,所选坐标序列平均跨度约为24年,数据缺失率较低,能够有效地避免数据缺失对噪声模型及速度估计的影响.
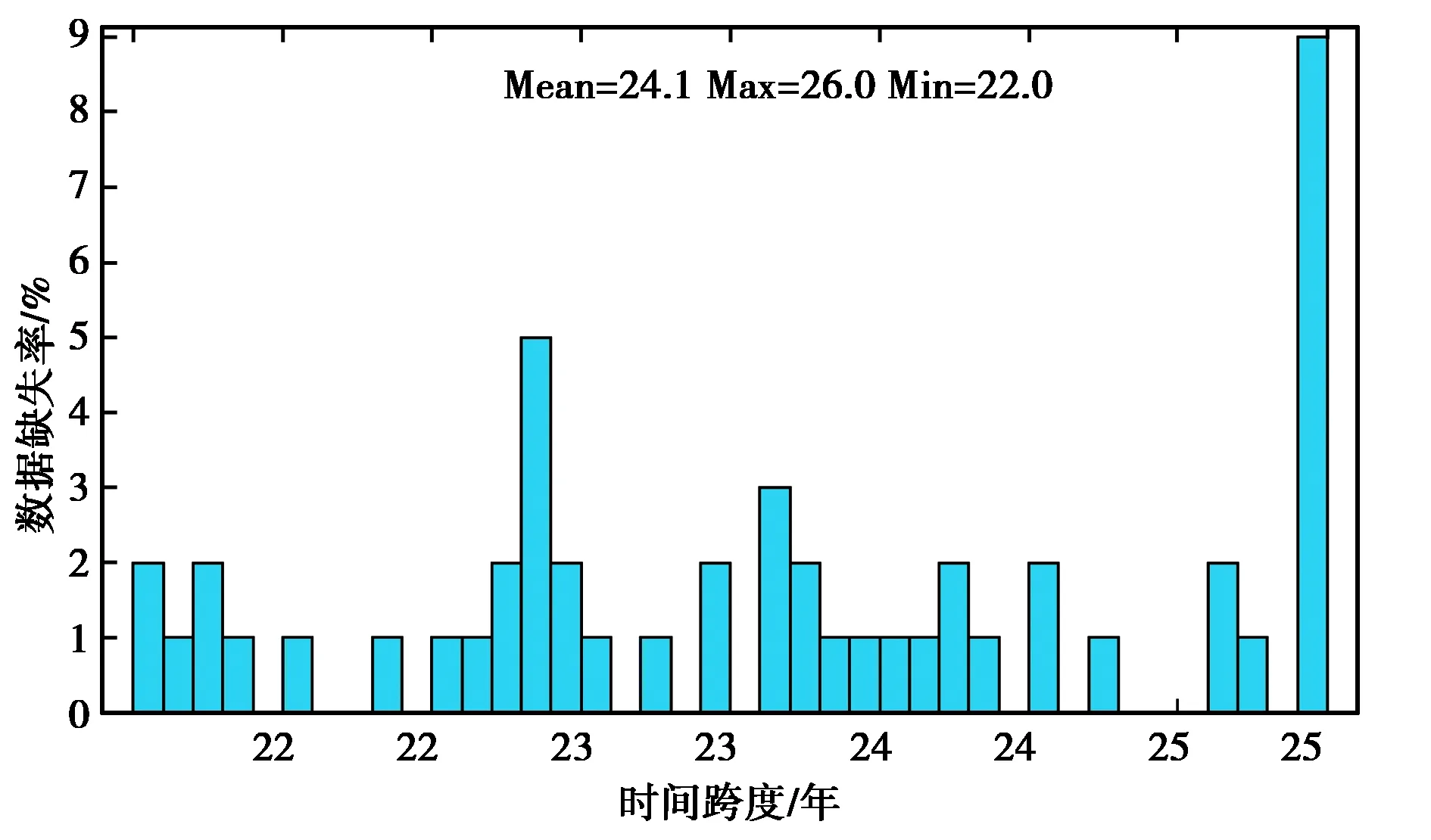
图1 所分析的IGS基准站坐标序列时间跨度信息
1.2 PCA/KLE空间滤波数学模型
IGS基准站时间序列中普遍存在共模误差,研究如何剔除共模误差带来的影响是分析IGS基准站时间序列特性的重要部分.PCA为一种非参数正交分解的处理方法,结合Karhunen-Loeve(KLE),对IGS基准站坐标时间序列进行滤波,以去除其中的共模误差.PCA/KLE空间滤波数学模型可表示为以IGS基准站的时间序列排列起来形成一个n×m(n>m,n为观测数或历元数,m为观测类型)的数据矩阵X,其协方差阵为CX,则CX=XTX.数据矩阵如下[10]:

(1)

若定义:
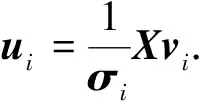
(2)
则表示为
(XTX)ui=λivi.
(3)
得向量矩阵:
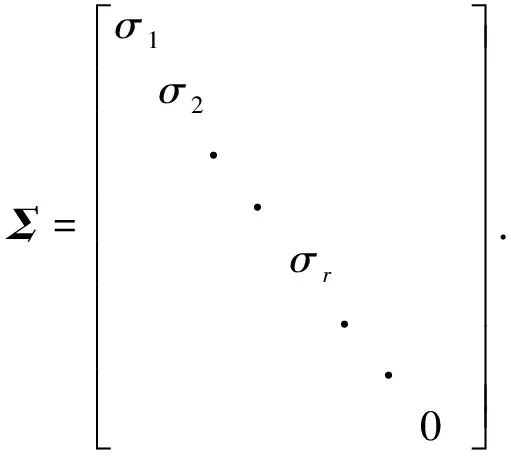
(4)
U=[u1u2,…,un].
(5)
式中:ui是n×1列向量;U为n×n向量矩阵;V为m×m向量矩阵,带入计算得:
Xvi=σiui,
(6)
XV=UΣ,
(7)
X=UΣVT.
(8)
令Λ=ΣTΣ,则有:
CX=XTX
=(UΣVT)TUΣVT
=VΣTΣVT
=VΛVT.
(9)
即V构成X的正交基底,矩阵X按照KLE展开可得:
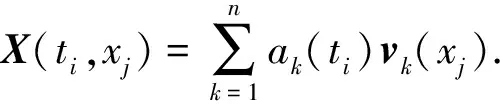
(10)
ak(ti)可由下式求出:
X=AV⟹A=XV-1⟹A=XVT,
(11)
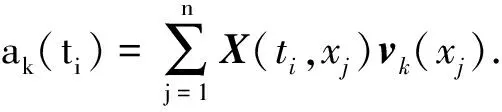
(12)
式中:ak(t)是第k个主成分;vk(x)是对应主成分的响应特征矩阵,分别代表时间特征和空间响应.
采取PCA与KLE相结合的PCA/KLE方法,充分利用了PCA能较好地提取时间序列的空间特性及KLE可从含有强烈本地噪声影响的时间序列中提取出连贯信号的优势,对IGS基准站坐标时间序列进行滤波,去除IGS基准站时间序列中的共模误差[11].
1.3 噪声模型估计
为了获取IGS基准站时间序列噪声模型估计的可靠性,本文采用赤池信息量准则(BIC)对滤波前后噪声模型进行最优模型的判定,BIC噪声模型估计原理[12]:
BIC=klnn-2lnL,
(13)
式中:n为样本数量;L为某一模型中的似然函数;k为模型变量;BIC越小,则对应的模型越接近最优模型.
1.4 IGS基准站速度估计
BOS[13]假设站速度用线性回归法拟合估计,噪声模型对站速度的估计影响可表示为
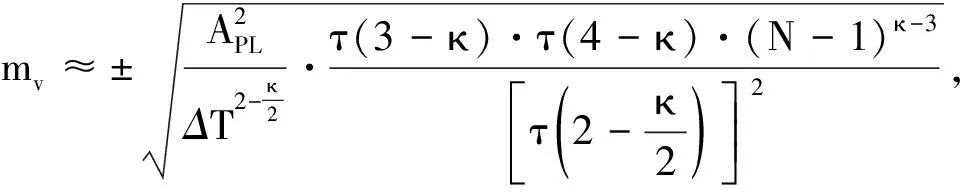
(14)
式中:N为观测值序列长度;κ为估计谱指数;ΔT为采样率;APL为噪声振幅;τ为伽玛函数.
1.5 周年项变化估计
IGS基准站坐标时间序列含有明显的周期性信号,这种信号主要表现出周年运动特征[14-17].台站周年项变化可以通过相位φ和振幅A来描述:
Asin[ω(t-t0)+φ],
(15)
式中:t,t0为时间;ω为周年角频率.
2 CME对噪声模型建立及站速度影响分析
2.1 CME对噪声模型影响分析
分别对所选的50个IGS基准站分别采用PL+WN、FN+WN、FN+RW、FN+WN+RW噪声模型进行滤波前后噪声模型估计,图2示出了BIC方法估计出的最佳噪声模型估计结果,分别为E、N、U坐标方向对应BIC值为最小值的噪声模型所占比例.
由图2可知,N分量滤波前后无FN+RW噪声模型,滤波前FN+WN噪声模型占比最大为66%,其次为PL+WN噪声模型,占比为30%,少量FN+RW+WN噪声模型占比为4%.对比滤波后噪声模型变化,PL+WN噪声模型占比增加至50%,FN+RW+WN噪声模型增加至14%,FN+WN噪声模型占比减少至36%,说明CME引起测站模型选择PL+WN作为最优模型,导致模型的有偏估计.E分量上滤波前后最优模型均为FN+WN,占比分别为50%,46%,PL+WN噪声模型滤波前比滤波后占比减少了8%,但FN+RW+WN噪声模型滤波后比滤波前占比增加了12%,说明随机游走噪声模型在E分量的影响不可忽略.U分量各噪声模型滤波前后占比变化较小,FN+WN噪声模型占比无变化,FN+RW+WN噪声模型滤波后比滤波前占比减少了2%,PL+WN噪声模型滤波后比滤波前占比增加了2%.综上可知,CME引起IGS基准站坐标序列模型变化且可能造成噪声模型的有偏估计,且在N分量与E分量上影响更为明显.
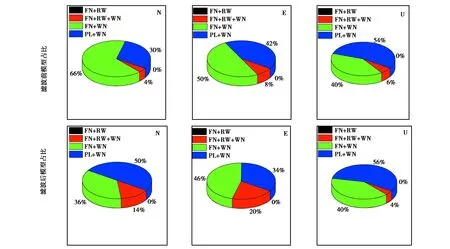
图2 IGS基准站台噪声模型占比分布图
2.2 CME对IGS基准站速度及其不确定度分析
进一步探讨CME对IGS基准站速度及其不确定度的变化规律.图3示出了CME滤波前后站速度估计对比分析结果.由图3可知,滤波前后不同噪声模型下站速度变化规律较一致.N分量上FN+WN噪声模型站速度值滤波前后部分站如CMBB站、FAIR站、QUIN站等曲线变化波动略大,FN+RW+WN噪声模型滤波前后站速度值变化较小,FN+RW噪声模型与PL+WN噪声模型站速度曲线变化规律类似;E分量上显示PL+WN噪声模型特性的站占比较多,其滤波前后站速度值变化较为明显,最突出显示的站有BRIB站、CLAR站、CSN1站、FLIN站、HOLP站、HOPB站、LBCH站、LONG站等,滤波后大部分站速度值在0上下波动;U分量上,各噪声模型站滤波前后速度值变化较小,90%的站滤波前后站速度不大于0.05 mm/a.
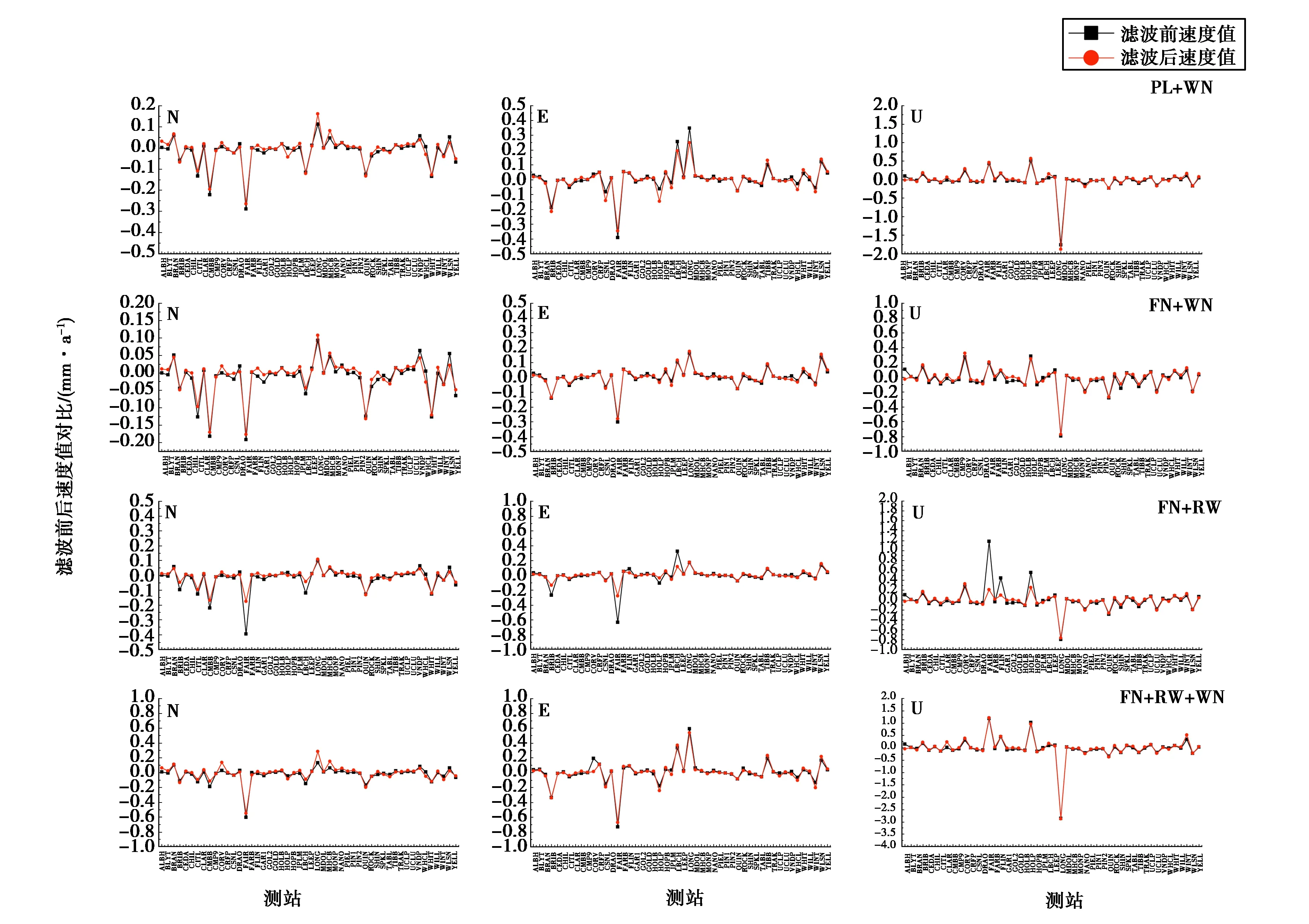
图3 滤波前后站速度变化规律
统计N、E、U三分量不同噪声模型下滤波前后站速度差值极值,如表1所示.
表1 不同分量站速度差值极值mm/a

极值类型NPL+WNFN+WNFN+RWFN+RW+WNEPL+WNFN+WNFN+RWFN+RW+WNUPL+WNFN+WNFN+RWFN+RW+WN最小值0000.00200000.0010.001 0.0020.001 最大值0.0490.0330.2190.156 0.0990.0290.353 0.1760.1140.137 0.9760.219 均值0.0050.0050.0120.014-0.0050.0020.008-0.0060.010.011-0.0200.016
如表1所示,滤波前后N分量PL+WN、FN+WN及FN+RW噪声模型站速度差值最小值均为0,且均值较小,FN+RW+WN噪声模型站速度差值均值最大为0.014 mm/a;E分量四种噪声模型滤波前后站速度差值最小值均为0,其中,FN+RW噪声模型中站速度差值最大为0.353 mm/a,但各噪声模型的站速度差值均值绝对值不超过0.01 mm/a;U分量FN+RW噪声模型的站速度差值极值比PL+WN、FN+WN、FN+RW+WN噪声模型大,且站速度最大值为0.976 mm/a.综上所述可得,CME对站速度变化影响较小,滤波后大部分站速度值在0上下波动,U分量上90%的站滤波前后站速度不大于0.05 mm/a,各噪声模型滤波前后各噪声模型站速度值变化较小.
进一步探讨CME对站速度不确定度的影响,CME滤波前后站速度不确定度差值变化规律曲线如图4所示.由图4可知,滤波前后N分量上四种噪声模型站速度不确定度差值曲线较稳定,约90%的站集中在0处,其中PL+WN噪声模型中HOLP站与LEEP站速度不确定度差值较为突出,FN+RW噪声模型中CMBB站、FAIR站、HOLP站与LEEP站站速度不确定度差值略大;E分量四种噪声模型站速度不确定度差值曲线差异较大,部分站经滤波后噪声模型特性由FN+WN变为FN+RW+WN,部分由PL+WN噪声模型特性变为FN+RW+WN,这种变化可能导致站速度不确定度的不稳定,其中CORV站、FAIR站、HOLP站、MDO1站及ROCK站变化较大,可能出现这种变化的原因是CORV站、FAIR站于2011年107年积日发生较大位移,CORV站、FAIR及HOLP站在U分量分别发生-11.037 mm、-9.519 mm及13.263 mm的位移,ROCK站于2013年在U分量发生4.132 mm的同震位移,ROCK站于2011年N分量与U分量分别发生最大为7.799 mm、-10.460 mm的同震位移,一部分站噪声模型特性由FN+WN、PL+WN变为FN+RW+WN噪声模型特性,说明FN成为站速度不确定度发生变化不可忽略的因素之一;U分量PL+WN、FN+WN、FN+RW+WN噪声模型站速度不确定度差值变化特征规律曲线较为一致,FN+RW噪声模型站速度不确定度差值变化略有差异.综上所述可得,CME对站速度不确定度在E分量影响较大,因此在准确估计站速度不确定度时必须考虑CME,否则可能导致过高估计站速度不确定度.

图4 滤波前后站速度不确定度差值对比
2.3 CME对周年项影响分析
探讨CME对IGS基准站坐标序列中周年项的振幅大小,图5为滤波前后不同分量上站速度不确定度差值对比,研究CME对周年项影响.
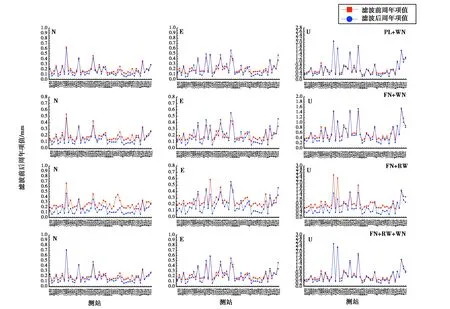
图5 滤波前后不同分量周年项值变化规律
如图5所示,不同分量上各噪声模型滤波后周年项振幅比滤波前周年项振幅值减小.N分量站周年振幅均不超过0.7 mm,其中滤波前后FN+WN与FN+RW噪声模型站周年振幅变化差值略大,FN+RW噪声模型站速度不确定度最大差值为0.319 mm;E分量各噪声模型滤波前后周年项振幅变化曲线类似,其中FN+RW噪声模型滤波后周年项振幅比滤波前周年项振幅值减小明显,滤波后约95%以上的周年项振幅不大于0.5 mm;U分量不同噪声模型周年振幅在0~2.5 mm之间,PL+WN、FN+WN及FN+RW+WN噪声模型周年项振幅差值较小,但FN+RW噪声模型中FAIR站、FLIN站、HOPB站、LONG站、WINT站、WLSN站及YELL周年项振幅变化较大,据SOPAC资料查询,其中FLIN站、WLSN站、WINT站及HOPB站于2011年在U分量分别发生了12.166 mm、-13.082 mm、-9.785 mm及34.641 mm的同震位移,FLIN站、LONG站及YELL站分别于2015年、2012年及1996年U分量发生了 47.623 mm、10.901级-15.559 mm的位移,说明在U方向,CME对IGS基准站周年振幅变化影响最大.统计不同噪声模型下的N、E、U分量周年振幅极值如表2所示.
表2 滤波前后周年项极值对比mm
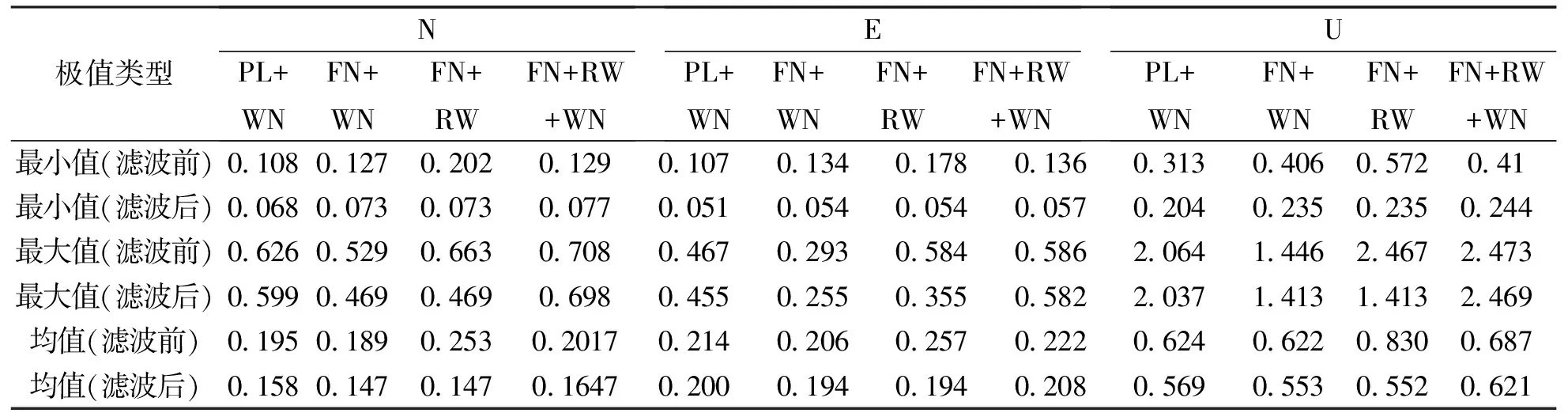
极值类型NPL+WNFN+WNFN+RWFN+RW+WNEPL+WNFN+WNFN+RWFN+RW+WNUPL+WNFN+WNFN+RWFN+RW+WN最小值(滤波前)0.1080.1270.2020.1290.1070.1340.1780.1360.3130.4060.5720.41 最小值(滤波后)0.0680.0730.0730.0770.0510.0540.0540.0570.2040.2350.2350.244 最大值(滤波前)0.6260.5290.6630.7080.4670.2930.5840.5862.0641.4462.4672.473 最大值(滤波后)0.5990.4690.4690.6980.4550.2550.3550.5822.0371.4131.4132.469 均值(滤波前)0.1950.1890.2530.20170.2140.2060.2570.2220.6240.6220.8300.687 均值(滤波后)0.1580.1470.1470.16470.2000.1940.1940.2080.5690.5530.5520.621
由表2可知,经滤波后各噪声模型周年振幅变小,N分量与E分量滤波后各噪声模型最小值均不超过0.1 mm,最大值不超过1.0 mm,均值小于0.2 mm;U分量滤波前后周年振幅比N、E分量周年振幅相对较大,最小值约为其他分量的4倍,最大值约为5倍,说明CME对站周年运动在U分量影响较为明显.
综上表明:1)CME对IGS基准站周年运动在U分量影响较大,且滤波后的周年项振幅比滤波前的周年项振幅小;2)FN+RW噪声模型滤波前后站周年振幅变化波动较大,滤波后的IGS基准站周年振幅较小,E、N方向IGS基准站周年振幅位移均小于1.0 mm,U分量上88%测站振幅位移小于1.0 mm,说明滤波后IGS基准站周年运动相对稳定.
3 结束语
本文以50个IGS基准站坐标序列为研究对象,并结合PL+WN、FN+WN、FN+RW、FN+WN+RW四种噪声模型,探讨不同噪声模型对IGS站速度及其不确定度估计的影响,得出以下结论:
1)所分析的50个IGS站坐标序列主要表现为FN+WN、PL+WN、FN+WN+RW随机特性,CME引起IGS基准站坐标序列模型变化且可能造成噪声模型的有偏估计,且对E、N分量的影响尤为明显.
2)CME对滤波前后站速度变化影响相对较小,U分量上90%的站滤波前后站速度不大于0.05 mm/a;CME对站速度不确定度在E分量影响较大,因此在准确估计站速度不确定度时必须考虑CME,否则可能导致过高估计站速度不确定度.
3)CME对IGS基准站周年运动在U分量影响较为明显,且滤波后的周年项振幅减小;E、N分量IGS基准站周年振幅位移均小于1.0 mm,U方向上88%测站振幅位移小于1.0 mm,说明滤波后IGS基准站周年运动相对稳定.对于地震活跃区域的测站,部分站表现为FN+WN+RW噪声模型特性,其影响机制有待进一步研究.
