航天器多舱段多组件结构系统整体式拓扑布局优化设计
2019-11-12郭文杰王立凯聂小华段世慧朱继宏
郭文杰,王立凯,聂小华,段世慧,朱继宏
(1. 中国飞机强度研究所,西安,710065;2. 西北工业大学,西安,710072)
0 引 言
结构拓扑优化技术经过30余年的发展和完善,在理论和工程应用中取得显著成就,已逐步成为结构概念设计阶段的一项重要技术,在提高飞行器结构性能、减轻结构质量上扮演着重要的角色[1~5]。尤其在航天器等包含部件舱段的结构系统的设计过程中,往往需要同时考虑组件设备的空间布局以及支撑结构的材料布局,这类同时考虑组件设备布局以及支撑结构材料布局的整体式拓扑布局优化问题已经引起相关学者的关注,并取得了一定的研究进展[6~13]。
结构系统的整体式拓扑布局优化设计问题面临的主要挑战是如何有效避免不同组件设备之间的几何干涉。工程中较为常用的方法是 Zhu[14]等提出的采用有限包络圆方法(Finite Circle Method,FCM)近似描述组件设备的外形,将不同组件设备之间的几何干涉约束转换为不同包络圆圆心距的约束,解决了几何干涉问题,但是为优化问题引入了大量的干涉约束函数,增加了求解的难度。一些学者提出使用 KS函数[15]等约束凝聚方法缩减约束数目,但对于处理包含数百个干涉约束的含有部件舱段的结构系统整体式拓扑布局优化设计问题还存在一定困难。
在前期工作的基础上[16,17],进一步将方法加以完善和改进,应用FCM描述组件设备的外形,应用多点约束技术(Multi-point Constraints,MPC)模拟组件、部件舱段、主体结构之间的连接关系,提出新的处理大量组件干涉约束的罚函数方法,以结构的整体刚度最大化为设计目标,对包含部件舱段、组件设备的航天器结构系统进行整体式拓扑布局优化设计。
1 优化设计模型定义
事实上,包含干涉约束的结构系统的整体式拓扑布局优化设计问题,一般以结构系统刚度最大化为目标,本工作引入的惩罚函数只对优化模型中的干涉约束进行处理,其他约束条件不予惩罚。考虑如下所示的约束优化问题:
式中f(x)为目标函数;gm为由 FCM 描述的任意一个干涉约束函数,这种形式的干涉约束函数的数目记为M。下文首先以传统的内、外点惩罚函数方法为例引出本工作提出的罚函数方法。
1.1 传统的内、外点惩罚函数方法[18]
对于上述优化问题,应用内点法可以将其转化为无干涉约束的优化问题,形式为
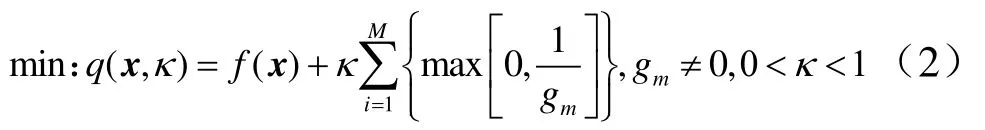
通过内点法,所有满足约束条件的非零约束函数都被以反比例函数的形式予以惩罚,这样的满足约束条件的解如果在可行域内部靠近了可行域边界,那么其惩罚项会被放大,构筑起类似于“高墙”一样的界限,阻止或避免解跳出可行域。
与内点法相对,根据惩罚函数的相关理论,传统的外点惩罚函数方法可以写成如下形式:
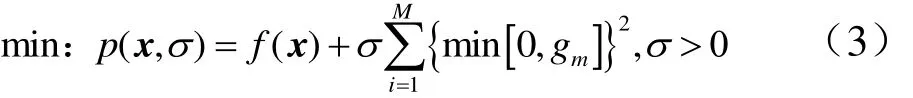
当约束违背约束条件后,由于二次函数的作用,其目标函数值被放大,优化算法在寻找新的极小值时,为了得到极小解,需保证惩罚项足够小,算法会违背约束条件的约束函数拉进或拉近可行域,从而起到惩罚的作用。
图1和图2为2种惩罚方法的原理性示意图。

图1 内点法原理示意Fig.1 Interior Penalty Term of gm
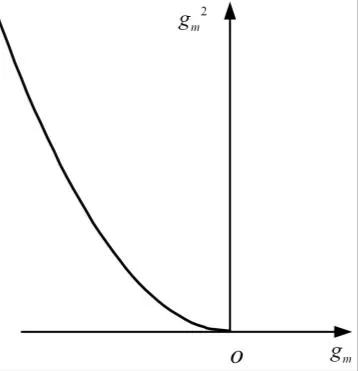
图2 外点法原理示意Fig.2 Exterior Penalty Term of gm
内点法能够处理的约束必须严格落在可行域内部,且初始点也需要落在可行域内部,在迭代过程中,每一组解都是可行域内部的解,可以作为原优化问题的近似解,但是,如果问题的解在优化过程中不慎跳出可行域,那么内点法就失效了;外点法以其构造简便、对初始点要求不高而被广泛应用于求解包含等式约束、不等式约束等问题中,但其在优化过程中只能对那些位于可行域外部的解进行惩罚,且最终获得的解往往位于可行域边界上,对于落在可行域内部的解其不做任何惩罚,也就是说对于已满足约束条件的解,外点法不能对其构成惩罚,无法避免解跳出可行域。
实际上,如果解在可行域外部,要将其拉进可行域,如果落入可行域内部,阻止其跳出,这样更利于优化问题快速得到最优解。
1.2 改进的惩罚函数方法
对于式(1),考虑构造一种形如式(4)的惩罚函数:

关于变量t的分段函数为
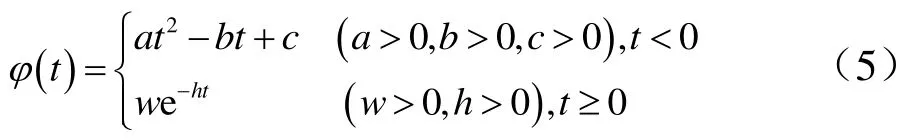
式中 a,b,c,w,h为分段函数控制参数。惩罚函数在约束条件满足时,用指数形式的函数实现对约束的微小惩罚,在约束条件违背时,用二次函数形式进行惩罚,违背越大,惩罚力度越大。
为便于优化算法求解,希望得到一种能够连续且可导的惩罚项,因为如果在分段点上函数不可导,则无法为避免组件干涉提供寻优方向。为了保证函数在t=0时的连续性和可导性,参数a,b,c,w和h必须满足一定的条件,即:
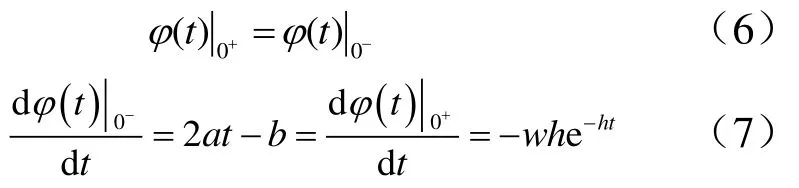
这样,可以得到控制参数之间的关系:


根据式(6)~(9),将包含大量非干涉约束条件的优化问题转化为不含非干涉约束条件的优化问题,减少了优化算法需要单独处理的约束条件的数目,为求解包含大量组件、大量干涉约束的多组件结构系统布局优化设计问题提供了有效的技术手段。分段函数如图3所示。

图3 惩罚项φ(t)示意曲线Fig.3 Curve of the Proposed Penalty Term φ(t)
由图3可以看出,整个函数的形态完全由二次函数的系数决定,这也表明所提出的方法具有较强的可控性,取二次项系数a为可变参数,取b和c为不变参数,不同a的取值下的形态如图4所示。

图4 不同a的取值下φ(t)的形态示意Fig.4 Illustration of φ(t) Under Different Values of a
在多组件结构系统布局优化设计中,当不同组件之间发生干涉时,违背了约束条件的干涉约束的惩罚程度大小由二次项系数决定,而且干涉程度越大,惩罚程度也会越大。与此同时,当干涉约束条件满足时,仍然有图4中o点右侧部分保证每个干涉约束都受到一定的惩罚,这就在一定程度上保证了组件不会因处于可行解时而不受约束地跳出可行域,在一般情况下设置b为一个非零正数,因为在干涉约束为0时,希望有一个明确的寻优方向,如果分段函数在自变量为0时有一个负的梯度,基于梯度的优化算法,将指引组件从干涉向分开的趋势运动。
1.3 多舱段多组件结构系统布局优化设计数学模型
本文应用 MPC[19]模拟组件与其支撑结构之间的刚性连接,引入多点约束技术后,多点约束方程和边界条件方程可以统一写成:

式中 H为由系统的有限单元、多点约束连接单元以及边界条件共同确定的系数矩阵;u为系统的总体节点位移向量。考虑多点约束方程后,修订后的系统势能为
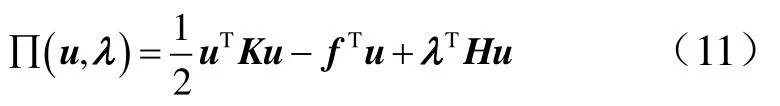
式中 K为系统的总体刚度矩阵;f为结构系统总体节点载荷矢量;λ为引入的拉格朗日乘子向量。求解式(11)的驻点为

求解式(12)可以得到位移向量u和乘子向量λ。在优化过程中,要考虑部件布局、组件布局、部件材料拓扑、主体结构材料拓扑这4类设计变量,即:
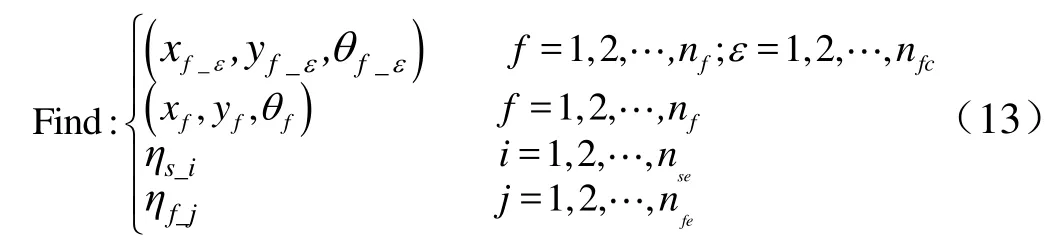
航天器多舱段多组件结构系统布局优化设计以系统的总体刚度最大化为设计目标,在给定部件隔框、主体结构材料用量以及系统质心位置约束的情况下,寻求合适的材料拓扑布局、组件、部件隔框的布局。可以表述为

式中 Vm,VmU分别为主体结构上拓扑优化设计所用材料体积分数及其上限;Vf,VfU分别为编号为f的部件隔框拓扑优化所用材料体积分数及其上限;xG为系统的质心位置分量;xGL,xGU为其上、下限。
为了避免部件隔框的组件之间、组件与设计区域边界之间、部件隔框之间发生干涉,用有限包络圆方法描述组件、部件隔框及其设计区域边界的轮廓,这种约束可以写成集合的形式:

引入改进的惩罚函数后,优化问题的目标函数以及约束条件可以写为

建立了包含部件隔框的多舱段多组件结构系统布局优化设计问题的数学模型。
1.4 灵敏度求解
本文提出了使用改进的罚函数处理大量的组件干涉约束,根据式(14)可知,目标函数的灵敏度包括2个部分,即:系统应变能及惩罚项的灵敏度,系统应变能灵敏度的求解过程可参见文献[17]、[18],惩罚项的灵敏度可根据式(7)求得,体积分数、质心位置等约束的灵敏度均可以根据其物理表达式求得。
2 数值算例
以某航天器多舱段多组件结构系统布局优化设计为例,证明本工作提出的方法的可行性。整个系统包含 2个可以沿舱体轴向 X平动的部件隔框 B1,B2和1个不可动部件隔框,每个隔框上布置3个互不相同的组件,各个组件在所属部件隔框上运动,隔框与其组件组成一个部件系统,组件与部件隔框之间、部件隔框与主体结构之间的连接均采用多点约束技术建立。
在整个筒体在顶部受扭矩T为300 N·m作用,扭矩通过刚性区域传递到筒体边缘,整个舱内承受0.1 MPa的内压力,为系统施加竖直向上的49 m/s2的加速度,整个筒体底边通过4个区域的节点完全约束。初始时描述部件隔框 B1和 B2距舱体底座距离的位置设计变量h1和h2分别设定为0.40 m和1.00 m,舱段总体沿X向高度H为1.50 m。组件初始在各自隔框情况如图5所示。

图5 航天器设备舱结构系统工况示意Fig.5 Load Condition Illustration of a Instrument Cabin System

续图5
组件几何模型及其有限包络圆划分情况如图6所示。

图6 组件几何及有限包络圆描述Fig.6 Discription of Components’ Geometry and FCM
系统材料属性如表1所示。

表1 舱体系统材料属性Tab.1 Material Property of the Cabin System
本算例中,每个部件隔框的设计区域边界用2个大小不同的同心圆描述,这2个同心圆形成了组件所在的环形可动空间,整个系统包含484个干涉约束,所有的干涉约束均用提出的改进惩罚函数描述。约束主体结构及部件隔框拓扑优化所需材料用量上限均为40%。
首先,不考虑系统的质心位置约束,联合组件、部件隔框、主体结构进行拓扑布局协同优化设计。如图7~9所示,最终所有组件、部件隔框协同主体结构共同承载并获得了清晰的结构构型和组件的不干涉位置布局。优化结果中h1=0.60 m,h2=1.20 m,系统的应变能C收敛于12.50 J。由于引入了内压力和扭矩,筒体上形成了许多环向的支撑筋,最上、最下设计区域面板均形成了分散着的支撑结构,部件隔框为支撑组件设备、筒体,形成了扇区一样的构型。优化结果中系统的质心位置为(0.680 m,0.0305 m,-0.0250 m)。

图7 第20次迭代,C=20.94JFig.7 The 20th Iteration, C=20.94J

图8 第40次迭代,C=13.85JFig.8 The 40th Iteration, C=20.94J
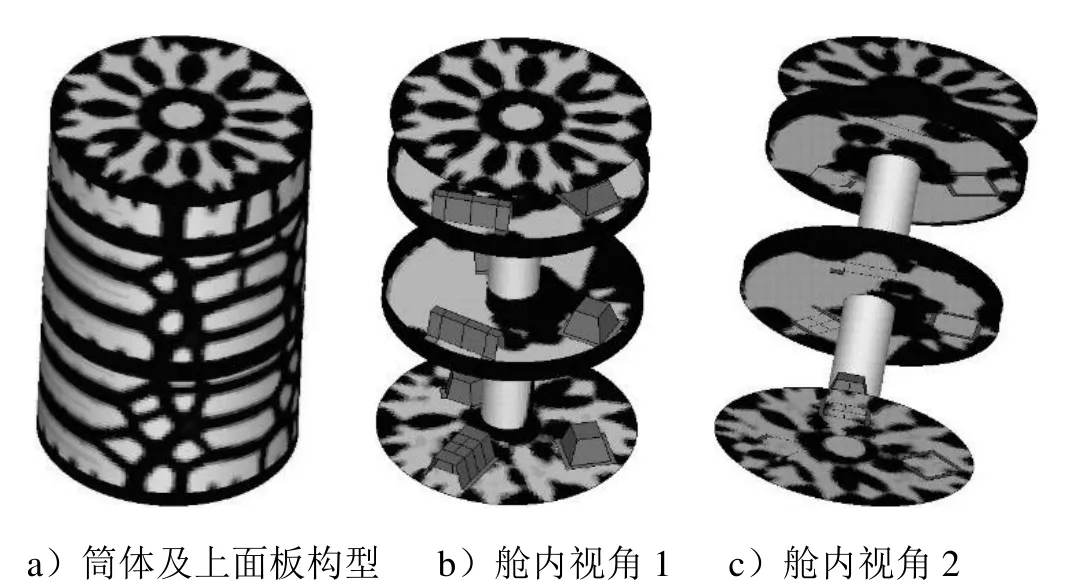
图9 优化结果,C=12.50JFig.9 Optimized Result, C=12.50J
由于整个筒体内各个组件在部件隔框上的可动范围不大,而且部件隔框的材料分布对筒体横向质心位置分量影响不大,引入系统在X轴方向上的质心位置约束,约束其上限为0.65 m。保持其余条件不变进行计算,系统最终的优化构型如图10所示。

图10 加质心约束的优化结果Fig.10 Optimized Design with Centroid Constraint
从图10中可以看出,与不加质心位置约束相比,本次优化结果中,其中靠下的一个可动部件隔框明显向下移动,以满足系统的质心位置要求,最终系统的质心位置为(0.637 m,0.0318 m,-0.0248 m),部件隔框的位置分别为:h1=0.39 m,h2=1.20 m。图11和图12分别给出了有无质心位置约束情况下系统的应变能迭代曲线和轴向质心位置分量变化曲线。

图11 系统的应变能变化曲线Fig.11 Design History of Global Strain Energy
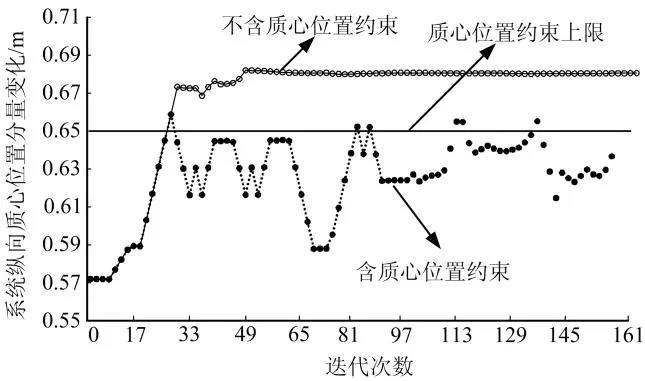
图12 系统X向质心位置变化曲线Fig.12 Design History of Centroid Position in X Direction
3 结 论
本文结合工程实际,描述了一种多舱段多组件结构系统,以传统的多组件结构系统布局优化设计研究为基础,建立了多舱段多组件结构系统布局优化设计问题的数学模型,为处理大量的组件干涉约束提出了改进的惩罚函数方法,并应用该方法完成了典型多舱段多组件结构系统的拓扑布局协同优化设计,验证了提出方法的可行性,拓宽了多组件结构系统布局优化方法的应用范围,对解决复杂工程问题有一定的参考意义。
