基于马尔可夫链的英语教学质量评价研究

摘 要：本文首先介绍了马尔可夫链模型的基本计算原理，通过对某高职院校2008、2010和2011级三个年级的英语高考成绩与英语应用能力A级考试成绩的状态转移统计及马尔可夫链分析，结果发现教学效果最好的是A级考试平均分居于中等的2011级，高考成绩与A级考试成绩平均分最高的2008级教学效果居中。

关键词：马尔可夫链;英语;教学质量评价

基金项目：本文系苏州卫生职业技术学院教改课题《高职院校英语教学质量评价研究》（课题编号：szwzy201301）研究成果。

1 引言

教学质量是学校人才培养质量的核心，是对教师的教学活动、教学效果进行价值判断的过程。学生考试成绩是对教师教学质量进行评价的一种方式，学校通常通过比较各平行班级学生的平均分与及格率来评价教师的教学效果。这种评价方式忽略了学生的原有水平基础。马尔可夫链评价方式在排除原有学习基础的条件下，衡量教师的教学效果，消除了由于学生基础差异外部条件、环境等因素而带来的影响，使评价结果的更为合理、可靠[1]。

2 马尔可夫链评价模型

马尔可夫链评价模型是一种基于概率论和随机过程理论，运用随机数学模型来分析研究对象发展变化过程情况的统计分析方法[2]。若某随机过程在t0时刻处于状态i，转移到t0+t时刻处于状态j，其转移矩阵只与时间间隔t有关，与状态i无关。在教学评价过程中，通过列出两次成绩，列出转移概率矩阵，得出最终分布情况。马尔可夫链评价方式去除了学生的原有基础因素，评估学生总体取得的进步程度與教学效果[3]。

在使用马尔可夫链进行评价时，首先要对学生成绩进行分级。一般总分100分，可分为优、良、中、及格、不及格五个等级，其中90-100分为优，80-89分为良，70-79分为中，60-69分为及格，0-59分为不及格，五个等级分别用n1、n2、n3、n4、n5表示。其次，在成绩统计中，用nij表示状态由ni经过一次转移后变为nj状态的人数，用向量表示学生成绩在t0和t0+t时刻分别所处的等级状态Pij=nij/ni（i，j=1，2，3，4，5）。Pij表示经过一段时间学习后，学生成绩从状态等级i转变为状态等级j的概率。根据随机理论，马尔可夫链在一定条件下具有稳定性，教师的教学效果可以用极限分布进行评价。由马尔可夫链的无后效性可以看出，学生成绩的进步与原有基础无关。

3 研究方法

本研究采用马尔可夫链模型分析法对比某高职院校2008、2010、2011年级学生的英语高考成绩与应用能力A级考试成绩的等级状态转移结果，分析各年级的教学效果与教学质量。

3.1 研究对象

本研究以某高职学院2008、2010级和2011级共三个年级每个年级340人共1020名学生为研究对象，每个年级选取护理、康复、医学检验、药学、口腔、眼视光和会计等六个专业江苏生源的学生。

3.2 分析方法

本研究材料主要选取三个年级学生高考成绩与大学一年级参加的高等学校英语应用能力A级考试成绩。因学生高考英语总分为120分，A级考试总分为100分，数据分析时将高考成绩折算为百分制再进行统计分析，通过运用马尔可夫链统计模型分析各年级学生的成绩的转移概率及极限分布，从而分析教学效果。

4 研究结果

4.1 高考与应用能力A级考试平均成绩统计

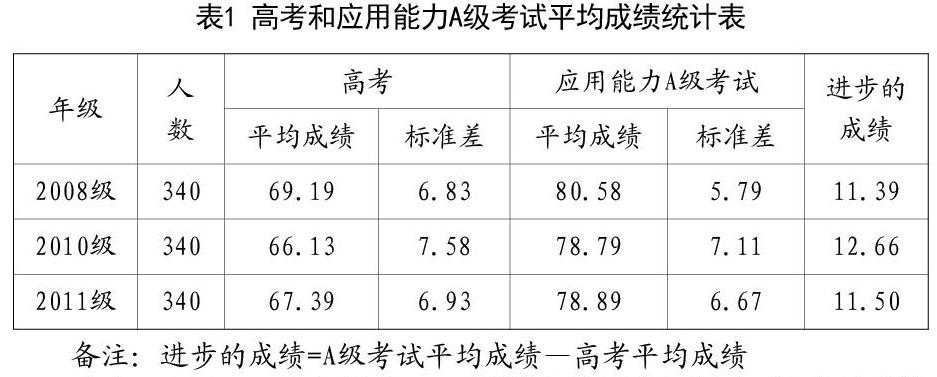
某高职学院2008级、2010级和2011级学生的高考成绩与英语应用能力A级考试成绩及进步的成绩统计表见表1.

由表1可见，三个年级中2008级学生英语应用能力A级考试成绩最高为80.58分，2010级与2011级成绩只差0.1分，2010级成绩最低为78.79分。但是从进步的成绩看，2010级进步的成绩最高为12.66分，2008级进步的成绩最低为11.39分。进步的成绩2008级与2011级只相差0.11分。由进步的平均分看2010级的教学效果最好。而由高考与应用能力A级考试平均分比较看，2008级学生的英语水平高于2010级和2011级。

4.2 高考与应用能力A级考试成绩马尔可夫链模型分析

根据表1中2008、2010和2011年级的A级考试平均成绩考虑教学效果，2008级最高，但这样的教学效果评价方式忽略了学生的原有基础。因此需要通过马尔可夫链模型分析不同年级的教学效果。

三个年级由高考到A级考试的状态转移情况见表2、表3和表4。

由表2、表3和表4得到三个年级的英语成绩转移矩阵分别为：

根据线性方程组求得2008级学生英语成绩分布向量为：

S1=（0.1133，0.6085，0.1440，0.00280，0.1133）;

2010级学生英语成绩分布向量为：S2=（0.1422，0.5421，0.1237，0.0487，0.1432）;

2011级的成绩分布向量为：S3=（0.0127，0.7948，0.1730，0.0068，0.00127）。

由上述向量分布可以看出，2008级学生的不及格率为11.33%，2010级学生的不及格率为14.32%，而2011级学生的不及格率为0.13%。从不及格率角度看，2011级学生的总体最好。为了量化教学效果，给五个等级分别确定分值为：优=90，良=80，中=70，及格=60，不及格=50。利用极限分布进行加权平均，得出量化值分别为：

S1=（0.1133*90+0.6085*80+0.1440*70+0.00280*60+0.1133*50）=75.87

S2=（0.1422*90+0.5421*80+0.1237*70+0.0487*60+0.1432*50）=74.91

S3=（0.0127*90+0.7948*80+0.1730*70+0.0068*60+0.00127*50）=77.31

上述量化值表明，在三个年级中，尽管学生的高考成绩和A级考试成绩2008级最高，但马尔可夫链模型显示2011级学生取得的进步最大，教学效果最好，而且三个年级进步的成绩总体没有显著差距，这也说明该高职院校的英语教学水平2011年有所提高。

5 结论

根据马尔可夫链模型分析某高职院校2008、2010和2011年级的英语高考成绩与应用能力A级考试成绩状态，可以看出教师的教学效果跟学生的原有基础并无太大关系，关键看学生所取得的进步。当然，学生的学习成绩评价只是教师教学质量评价的一部分，要全面衡量教师的教学质量还要考虑教师的教学内容、方法手段及对学生自主学习能力的培养等。

参考文献

[1]彭志行，马红霞，赵杨，易洪刚，娄东华，于浩，陈峰.马尔可夫链模型在医学高等教育教学质量评价中的应用研究[J].中国高等医学教育，2009（5）：22-24.

[2]万里亚.马尔可夫链在教学质量评价中的应用[J].南通职业大学学报，2011（6）：67-69.

[3]张雅清.马尔可夫链在教学质量评价中的应用[J].湖北广播电视大学学报，2010（3）：128-129.

作者简介

郭新月（1975-），女，江苏如皋人，讲师，苏州卫生职业技术学院教师，研究方向：英语教学法。